Overview and Background
Finite Difference Time Domain (FDTD) Modeler
FDTD techniques are often the method of choice for modeling unbounded complex inhomogeneous geometries. It is a time domain based model allowing transient analysis.
However, infinite precision variables requiring floating point arithmetic are implicit in their formulation making it difficult to implement them in a completely parallel fine-grain computing environment. [Bridges, Simons]
Yee replaced the partial derivates in Maxwell's curl equations by central finite differences. The Yee cells discretize the electric and magnetic fields into components on the cell as in the below figure.
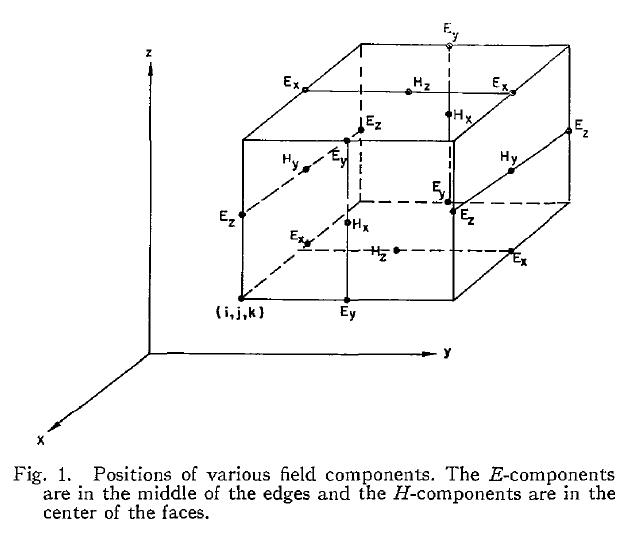 At every time step each cell is updated with a new value for the E and H fields. The space grid size must be only a fraction of the wavelength of the electric field in order for the solution to be stable. Therefore there is a restriction imposed on the grid size by the time increment. [Yee]
At every time step each cell is updated with a new value for the E and H fields. The space grid size must be only a fraction of the wavelength of the electric field in order for the solution to be stable. Therefore there is a restriction imposed on the grid size by the time increment. [Yee]
LGA's are a class of cellular automata algorithms consisting of an extremely large regular lattice of interconnected cells. Only a few bits can be used to define the entire state of the cell. Any integrable vector field can be described in terms of flow of imaginary particles. [D Hiebeler, R Tater]
When mass and momentum are conserved in the microscopic interactions, the macroscopic behavior is shown to obey the two dimensional linear wave equation. [Margolus]
Most work of modeling electromagnetic dynamics was done by [Bridges, Simons]. Their work consists of modeling EM dynamics using integer lattice gas automaton which they compare with TLM (Transmission Line Matrix) models. They also propose a 3D EM modeling LGA which is compared with FDTD and TLM solutions. However, they indicate that the 3D model has not been verified whether the macroscopic behavior obeys the Maxwell's equations.