Brandon Martin-Anderson :: 862.13 final project
Sonar-scanning usine a Macbook: synethetic aperture sonar using consumer electronics
What is the goal?
Apply the techniques of synthetic aperture sonar (SAS) to image objects using common consumer electronics.
To accomplish this, what question(s) will you answer?
What is the best frequency for SAS in air?
A chirp at 20 kHz as output by Macbook Pro speakers is sufficient for about ~10 cm resolution at a range above 10 meters.
Do common speakers work?
Yes! Large speakers are not good at pushing loud chirps, but surprisingly tinny laptop speakers have a good high-frequency resolution, and are able to deliver a pulse less than 10 cm long.
Is the temporal resolution of cheap equipment sufficient for sonar?
Surprisingly yes. The fidelity of laptop speakers and microphones are sufficient to resolve sonar images.
What technique(s) will you use to answer them?
A Python script was written to deliver and record a train of chirps. The chirps were delivered by rolling a laptop along on a rolling chair, and the resulting matrix of was processed in Python using a brute-force algorithm to focus a single plane of reflectance values.
Python scripts for generating, recording, viewing, and analyzing sonar pings are here.
What is the prior art?
Synthetic aperture sonar is well-established in practice. Gough and Hawkins provide a good survey. Synthetic Aperture Sonar on Wikipedia.
To the best of my knowledge, there is no prior art for performing SAS using a laptop on a rolling chair as the towfish.
How will you evaluate the results?
The goal is to produce an recognizable image, with a feature size on the order of 10 cm.
April 22
Gathered speaker, microphone, and microcontroller. Next: program microcontroller to deliver and measure pings. Afterward: write signal analysis software to combine pings into an image.
May 14: Reading pings
Sent and received pings. The highest frequency ping output by my speaker is relatively low. It would be nice to find a solid-state sound transducer.
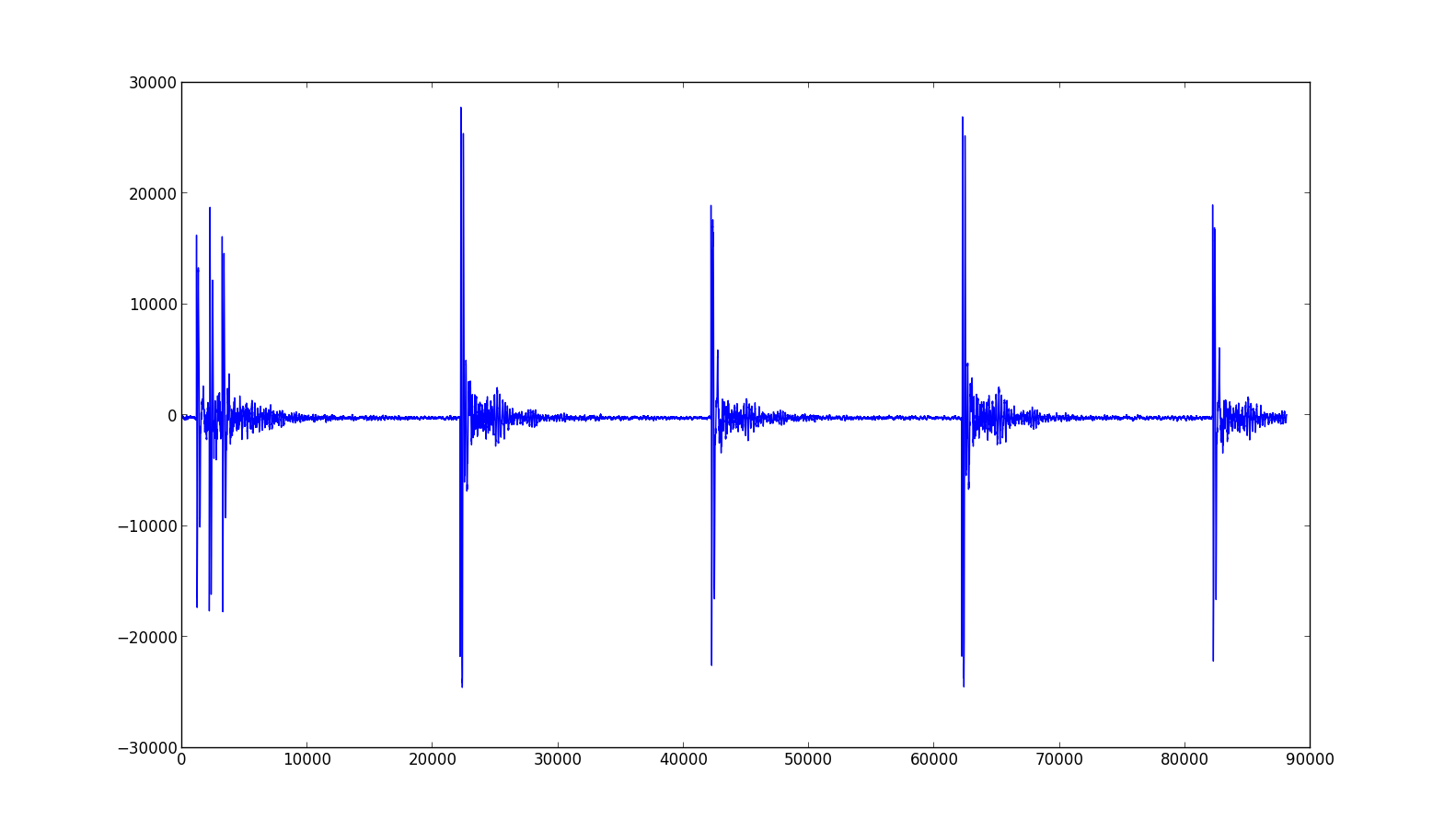
May 15: Scanning a room
The resolution of the speakers and microphone on my mid-2012 Macbook Pro turn out to be sufficient for sending and recording sound pulses in the 20 kHz range. Sending a step function to the speakers results in a sharp attack followed by a reverberation much lower in the audible range. The audible reverberation has the same approximate frequency as many sources of environmental noise (air conditioning, people talking etc) and isn't very useful for sonar, but echoes from the 20 kHz attack are easily detectable after isolation with a high pass filter. The following image shows the primary ping and a number of echoes corresponding to my chest, nearby people and objects, and the wall behind me. The resolution is quite good - loud attack pulse and corresponding echoes are about 180 microseconds long, corresponding to about 6 cm. Note the x axis scale is in samples (at a rate of 44100 samples per second), and the y axis scale is arbitrary.
The next step is to make a series of recordings of constant duration while traveling in a straight line at constant speed. In the following diagrams the x axis is recording duration, the y axis is distance, and the color dimension is range-compressed sound intensity. Each sample is approximately 0.07 seconds long.
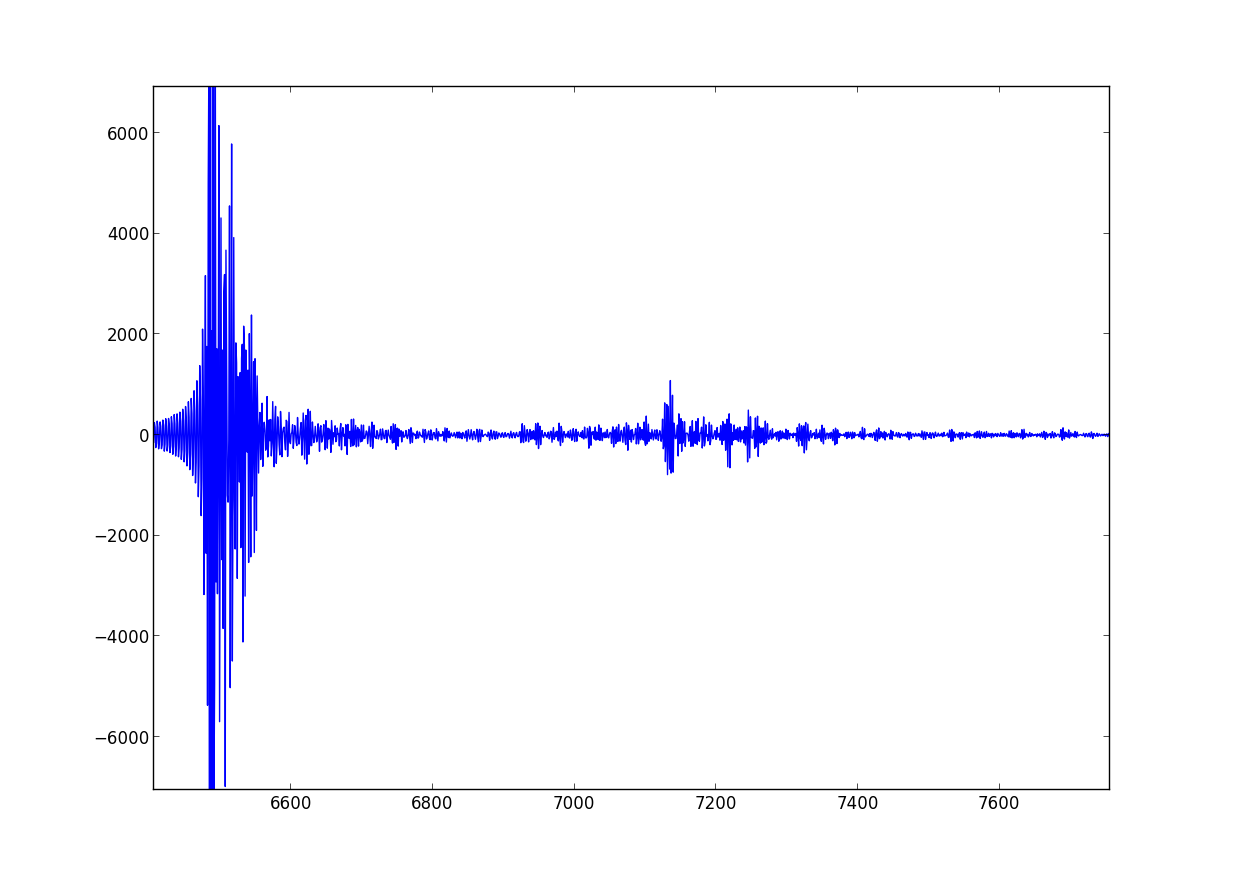
Small room, no movement.
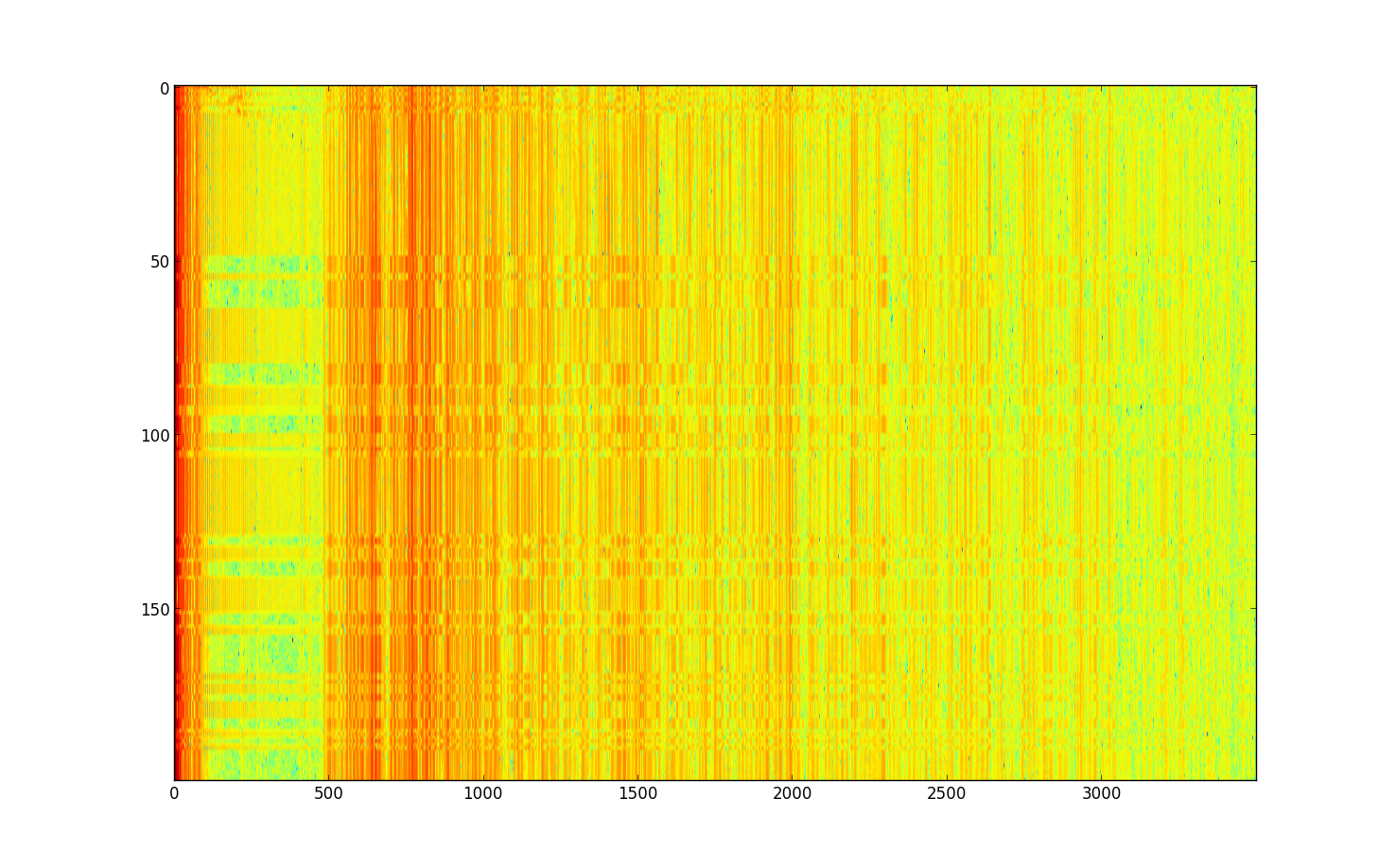
Small room, dragged laptop across table, 200 samples.
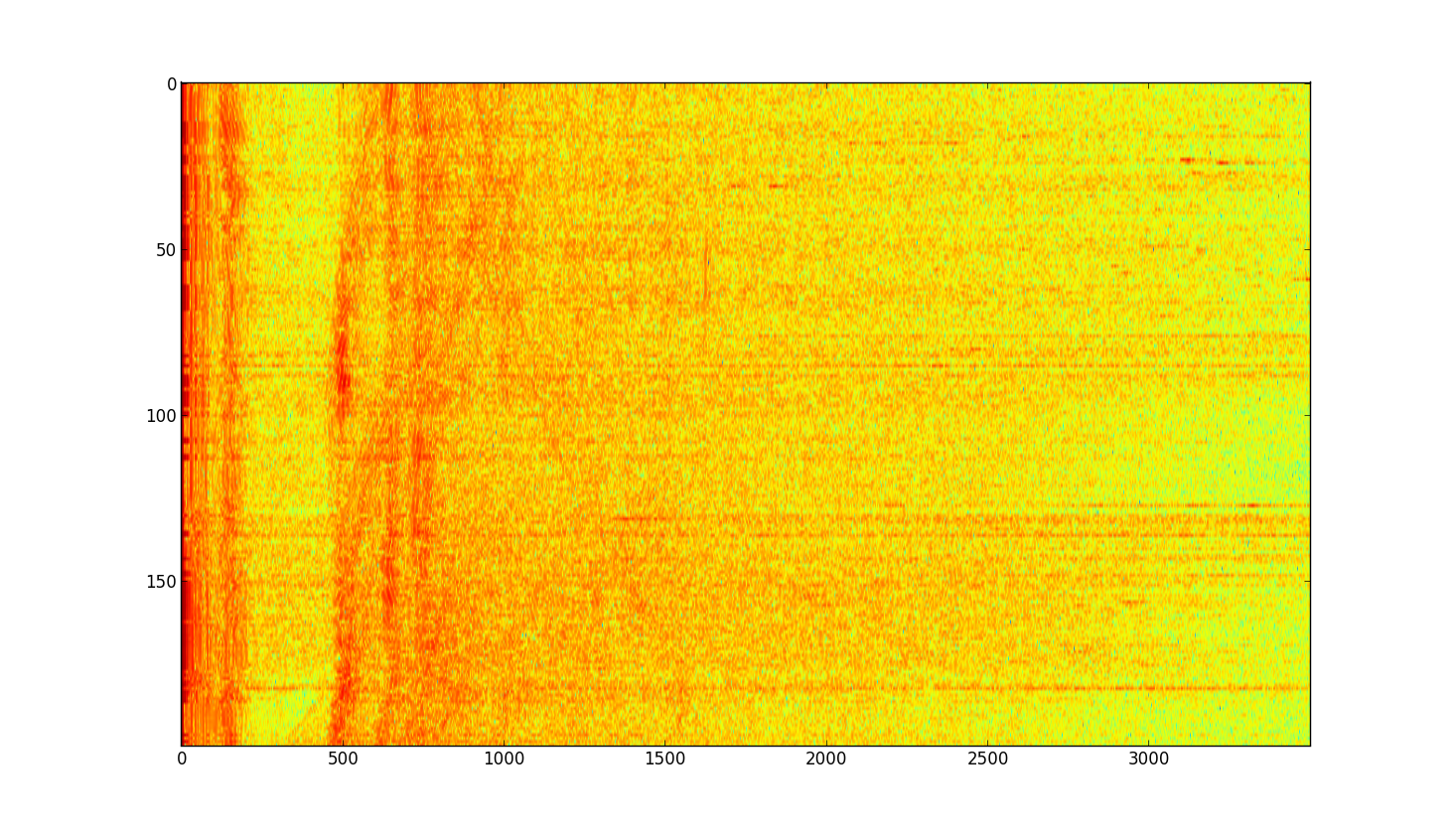
Large room (E14 atrium), walked slowly holding laptop, 300 samples. Note the ceiling echoes wobble because of variation in height while walking.
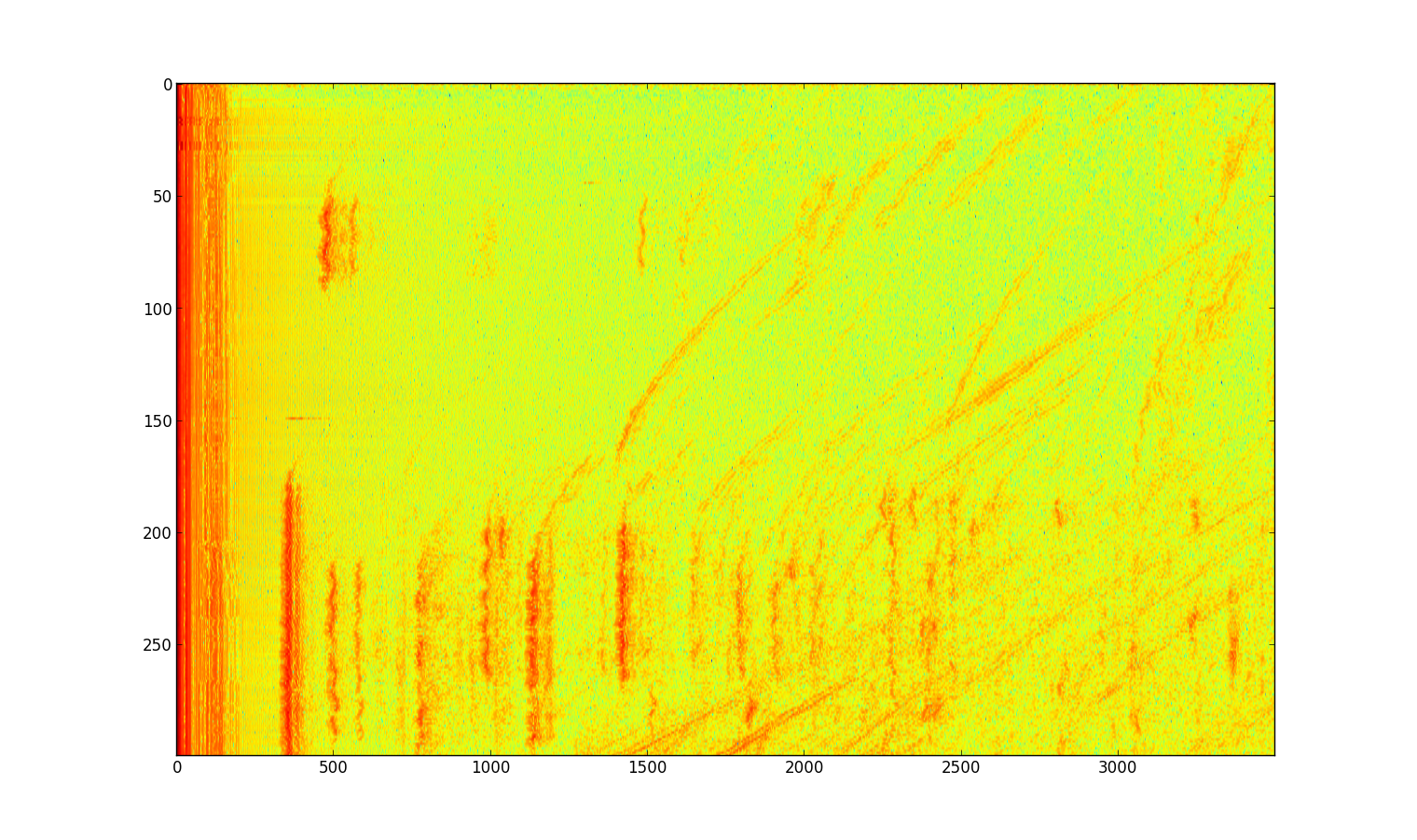
Large room (E14 atrium), pushed laptop on rolling chair, 300 samples.
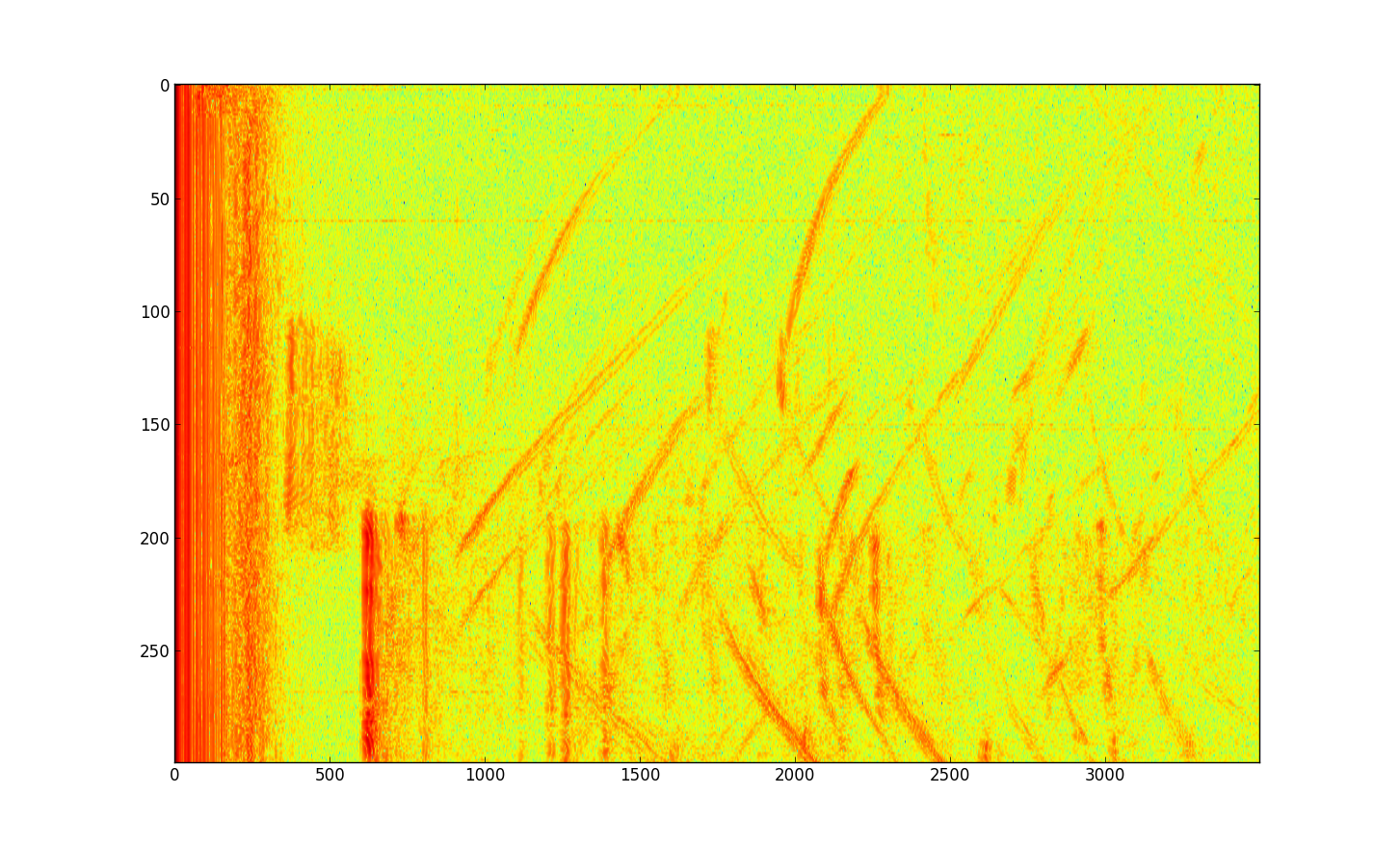
May 19: Calculating the image
Most literature on synthetic aperture sonar deals with imaging a universe consisting entirely of a plane of point reflectors parallel to a linear sensor path. This is a reasonable simplifying assumption for satellites imaging the surface of the earth or ships imaging the sea-floor, but satisfactory scenes are difficult to find inside a building. The outside of a building arrayed with depressed windows makes an excellent scene, however. The plane formed by the inset windows can be cleanly formalized as a plane of point reflectors, as inside corners tend to reflect beams straight back at their source regardless of incidence angle. The eastern face of building 66 was selected for imaging.

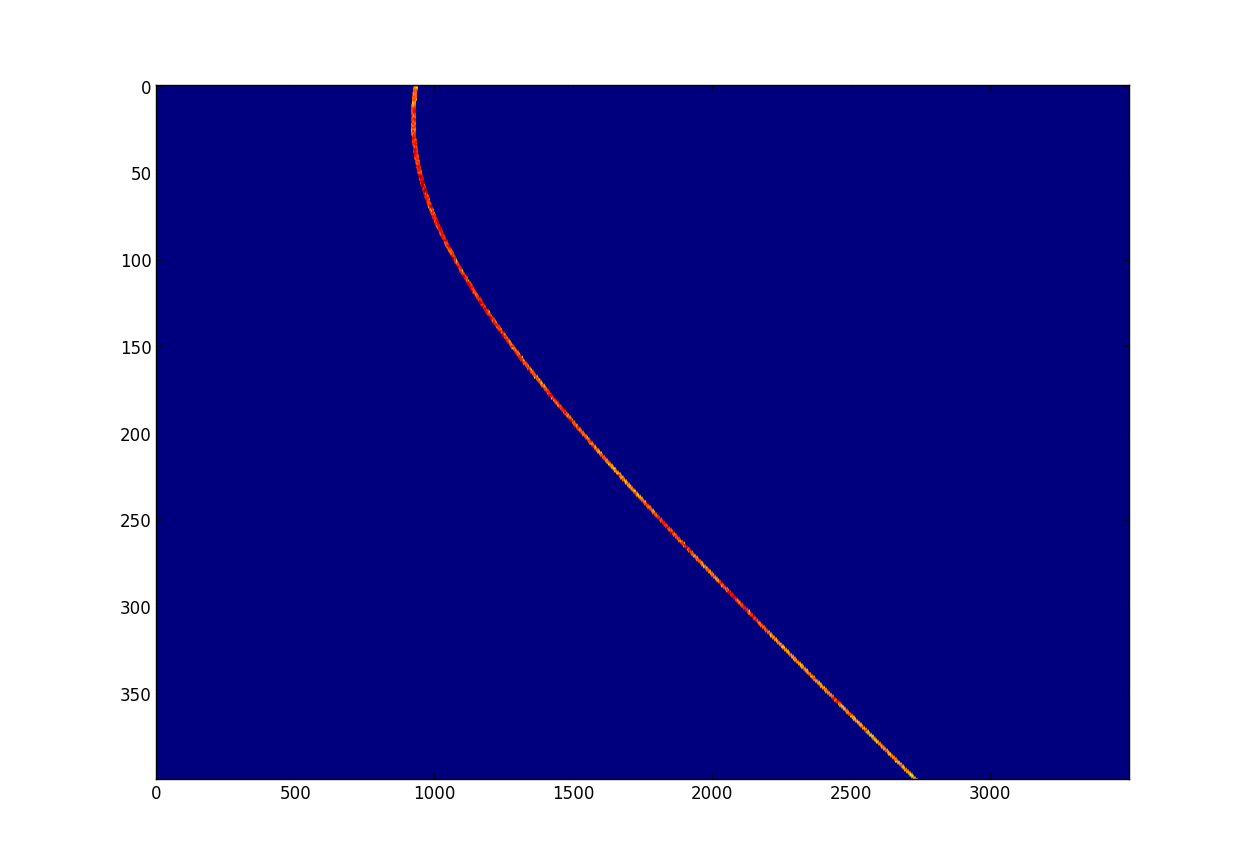
A sonar run was recorded by a laptop on a rolling chair (the "towfish" using SAS terminology), taking 400 samples over 10.4 meters. The laptop was 2.0 meters from the plane of windows, traveling in a line parallel to the plane, to the best of my ability given that I was walking without any registration. The range-compressed data ss(t,u) is shown below (where the range-compressed signal r(t)=log(abs(f(t)))), with the first sample ss(t,0) at top.

Rolling-chair-based towfish.
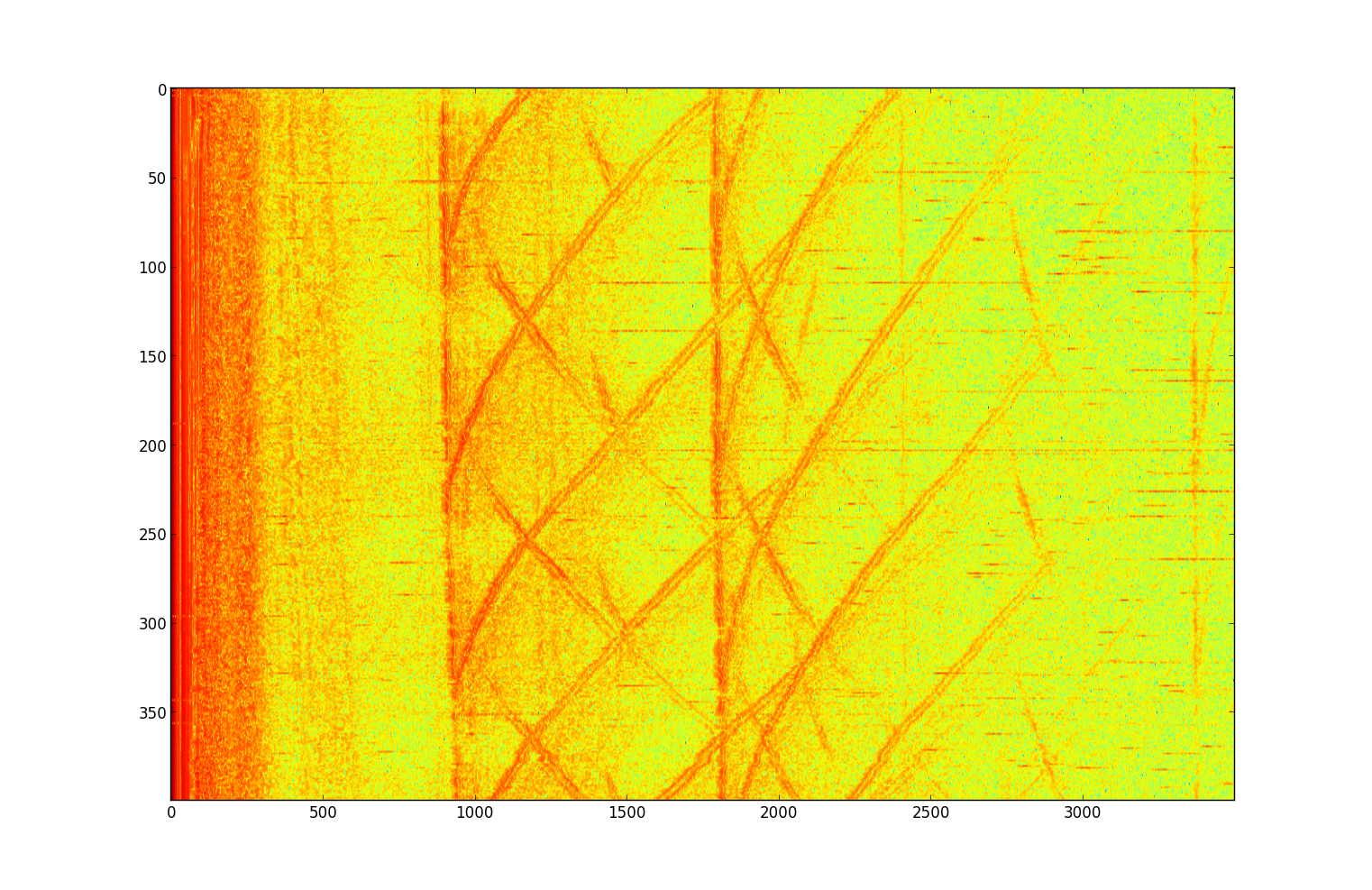
ss(t,u) of building 66 exterior
A few things jump out on inspection. I wasn't able to keep the towfish path perfectly parallel to the window-plane, resulting in some drift. Additionally, variation in speed results in some deviation of echo paths from perfect parabolas. Finally, I using both speakers of the laptop spaced about 30 cm apart results in a double echo for all point reflectors.
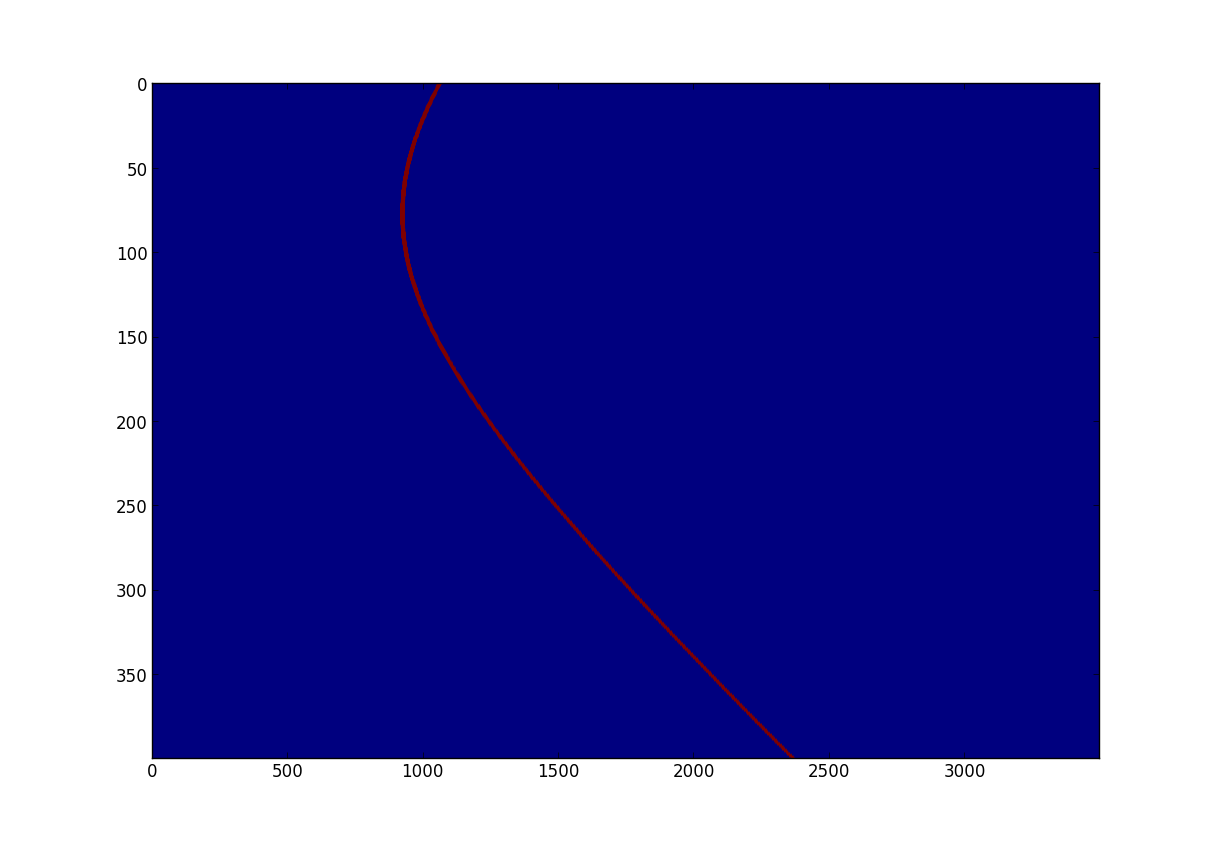
The task at this point is to convert the above data ss(t,u) into a two-dimensional reflectance function ff(x,y) describing some portion of the window plane. One particularly straigthforward algorithm involves producing a function ss_xy(u,t) with respect to a single point (x,y) in the imaged plane. It is straight-forward to construct a function ss_xy(u,t) with a constant pulse width and amplitude regardless of distance or beam orientation. For example, here's a ss_xy(u,t) function for a point reflector at (2.9,2.0), with 400 samples over a 10.4 meters, a depth of field of 2.0 meters, and a pulse width of 0.0004 seconds (~13 cm).
Next, multiply this template by the original ss(t,u).
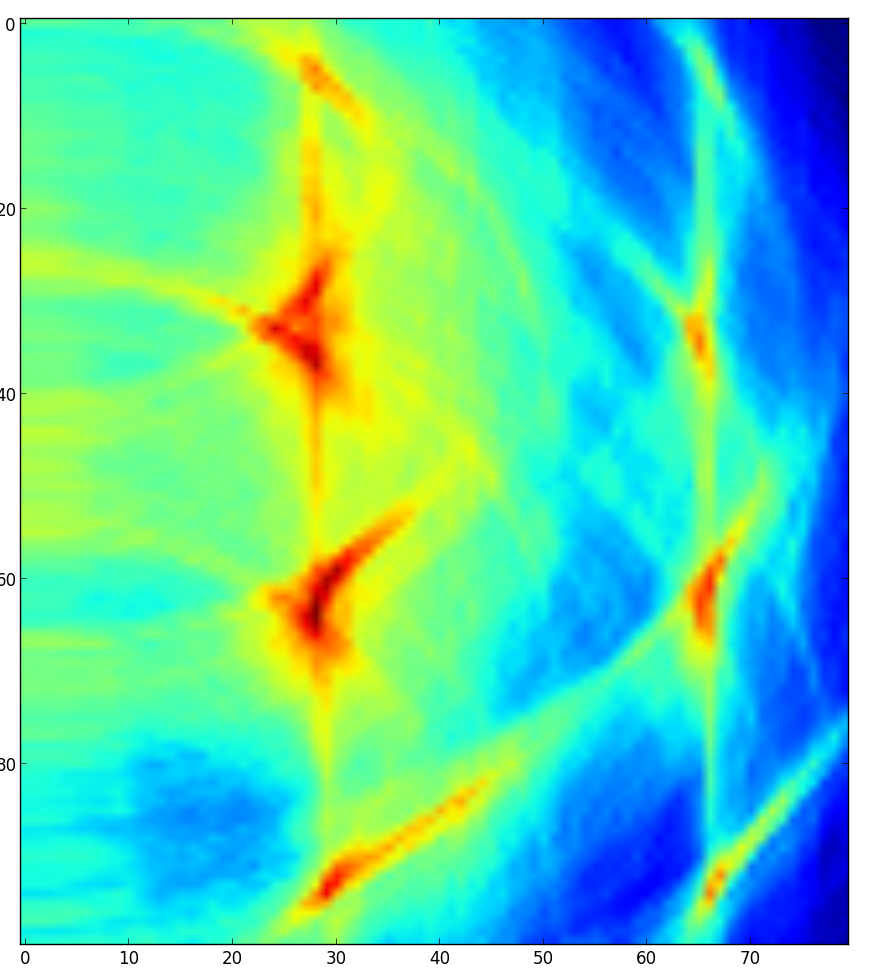
Integrating this function results in the reflectance of the point (x,y). Because we're interested in an unscaled reflectance function ff(x,y), it's sufficient to simply take the sum over all elements in the discretized function ss(t,u)*ss_xy(t,u). Repeating this process for the rectangle where x in the interval (0.0,8.0) meters with a resolution 0.1 meters and y in the interval (0.0,10.0) both with a resolution of 0.1 meters results in the following matrix of reflectance values.
By convention the towfish path is in the y axis of ff(x,y). Here's the same image rotated and overlayed on a photograph of the imaged site.

Note the bottom of the image corresponds to the height of the rolling chair that served as the towfish vehicle. The inside corners of each window visible directly from the towfish are extremely reflective, drowning out nearly every other feature. Point reflectors outside the focal plane are not visible, and mentioned data irregularities limit the smallest resolvable feature size. The scale, in decimeters, indicates that each window is about 3 meters high, which in fact they are.
Future improvements
Improvements to the straightness and parallelness of the towfish path, in addition to ensuring a constant towfish speed, would help to improve image fidelity. The greedy algorithm used is extremely slow - it took nearly an hour to produce the 100x80 image of the building 66 exterior. The hypothetical ss_xy(t,u) function is very crude; a more sophisticated function taking into account dropoff as a function of distance and beam angle would help reduce artifacts in the final image.
It would be thrilling to produce a SAS app that runs on smartphones and works off of a non-straight towfish path determined by the smartphone's intertial measurement unit. Such an app would have a number of assistive and games applications.