What is the Channel Capacity of the Human Bloodstream?
Abubakar Abid

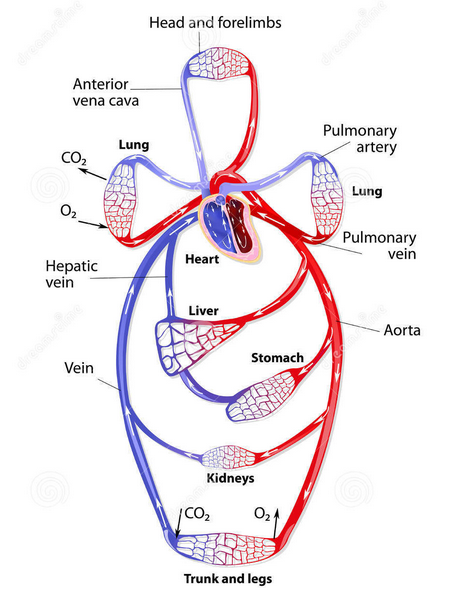
If the circulatory system is viewed as a channel, it is natural to ask - what is its channel capacity? How much information can be sent through this system? Unlike a traditional abstract communication channel, the circulatory system has geometry-dependent properties, because competiting processes such as diffusion and advection occur at different length scales. As such, it becomes critical to specify between which nodes (e.g. organs) we are interested in computing the channel capacity. For our purposes, we will start by determining the channel capacity between the pituitary gland and kindey in the presence of diffusion, advection, and absorption.

Specifically, my goals are to:

1. Define information and entropy within the context of molecular communication
2. To model the various transportation phenomenon that are occurring in the bloodstream.
3. To understand the time scales at which cellular signal transduction can occur and use that to derive a bandwidth for molecular communication.
4. To understand and model the sources of noise in the molecule-bloodstream system.
5. To derive an analytical expression for the channel capacity that depends on geometric and biological factors.
6. To derive a numerical estimate of the channel capacity between the pituitary gland and kidneys, and potentially other organs as well.

Work in Progress:

1. Define information and entropy within the context of molecular communication
In molecular communication, information is conveyed through the presence or absence of signaling molecules as a function of time [XX]. This can take different forms in the human body - for example, the presence of neurotransmitters can cause a neuron to undergo an action potential [XX]. Although the concentration of signaling molecules can convey information, in most cellular contexts, the receiving cell has no direct way of measuring this concentration. Instead, the concentration corresponds somewhat to a probability of detection, or to the probability that a particular cellular threshold has been reached (e.g. the threshold to fire an action potential).

We may choose to represent the time-sequence of molecules, $$m = {m_0, m_1, m_2 ...}$$ as a sequence of real-valued numbers between 0 and 1, representing a normalized concentration. In turn, the receiving cell maps these molecules as a sequence of signals $$s = {s_0, s_1, s_2 ...}$$ which we can represent as a binary sequence of only 0s and 1s. An intuitive mapping function would be something of the sort \(s = \left \lfloor{x+\frac{1}{2}}\right \rfloor \), but it could take a variety of forms - linear or non-linear, biased or unbiased, time-invariant or even time-varying. We do not concern ourselves with the mapping here, nor do we concern ourselves with how the cell interprets or acts on the signals it receives.

Let us assume that the probability of receiving signals is not time-varying, so let \(p_0\) be the probability that the cell receives signal 0 and \(p_1\) be defined likewise. In this representation, information and entropy take their familiar forms, where information in getting a signal of 0 and 1, respectively, is $$ I_0 = -\log{p_0}, I_1 = -\log{p_1}$$ And the entropy of this system is: $$H(p) = -p_0\log{p_0} -p_1\log{p_1}$$

2. To model the various transportation phenomenon that are occurring in the bloodstream
Because the signal is carried by molecules in cellular communication, it is important to be able to model the way that signal is carried and distorted from the transmitting node to the receiving node. In particular, there are three important processes that are occurring when molecules travel through the bloodstream: advection, diffusion, and absorption (or removal). For simplicity of this analysis, we can treat transport through the bloodstream as a 1-dimensional problem, where all movement is occurring in the direction of the blood flow. In this case, we assume that advection is entirely in the x-direction (see Figure below), which is reasonble, since the blood flow velocity in the axial direction can never be high due to boundary conditions on the vessel walls. We assume the same for diffusion, which is reasonable, because of the narrow width of the blood vessels ensuring a homogenous molecule concentration in a short period of time. Absorption/removal is due to a variety of factors, including molecular absorption by the vessel walls, as well as by major organs. In this case, we assume that this absorption occurs in a continuous distributed fashion, and is proportional to the concentration of the molecular signal.

Taking all of these factors together, we write the master diffusion equation as [XX]: $$ \frac{dc(x,t)}{dt} = D\frac{d^2c(x,t)}{dx^2} - \frac{d (v(x) c(x,t))}{dx} - rc(x,t)$$ Where \(D\) is the diffusion constant for the signaling molecule, \(v(x)\) is the velocity of blood flow, which is assumed to be time-invariant in a particular part of the body (where steady state has been reached), but is potentially varying across the circulatory system, and \(r\) is the removal absorption rate.

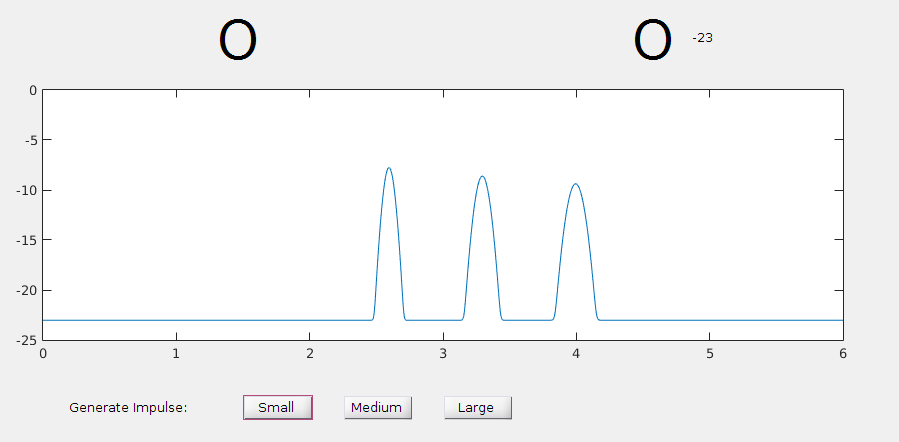
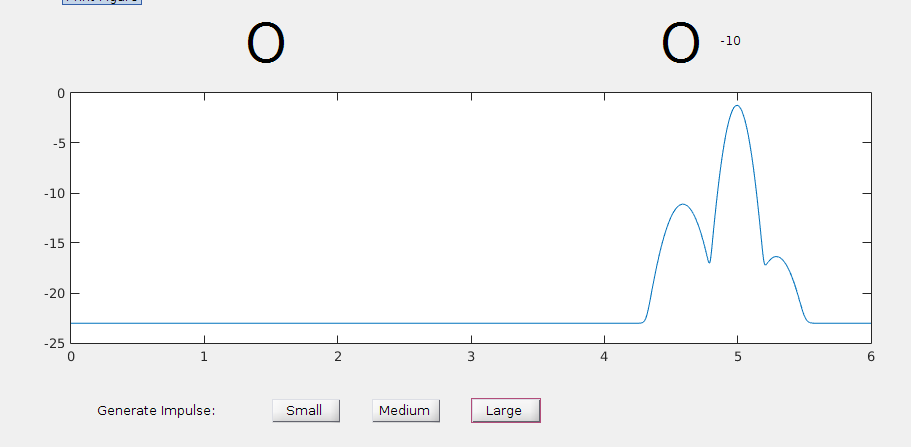
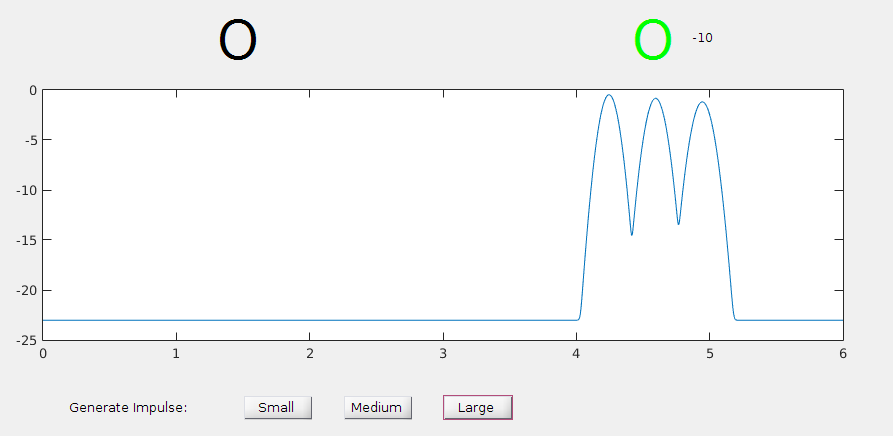
Now, this equation cannot be solved analytically. However, we are not interested in the complete solution. We are only interested in the concentration at a particular receiving location, \(c(x_r,t)\) with the initial condition being an impulse concentration (representing a transmitted signal) at x=0 on top of a background steady-state concentration of molecule, which is the result of an equilbrium between the build-up due to released molecules over time and the rate at which molecules are removed by the absorption in the blood vessel walls and major organs. $$ c(x,0) = A\delta(x) + c_0$$ Now, let us consider the three processes separately.

• Advection

Advection occurs entirely due to transport by the blood vessel. Although the velocity is time-varying, we can write the average velocity between the transmitting node and the receiving node as \(v_{avg}\), which is defined by $$v_{avg} = \frac{\int_0^L{v(x) dx}}{L} $$ Calculatig this average velocity is less important than establishing that an average velocity exists, and that as long as the blood vessels that branch out are identical in length and diameter, then this average velocity can be considered as applying to all of the particles that reach a point \(L\) in the circulatory stystem. The impulse response at point $L$ can be given by: $$ h(x,t) = \delta(x-v_{avg}t,t)$$

• Absorption
Hormones released into the bloodstream also experience absorption due to blood vessels and major organs that the blood vessels feed. We will model this absorption as occurring in a distributed fashion, where hormones are continuously released from the blood stream at a rate of \(r\), which is proportional to the concentration of hormones in the blood. Thus, \(r\) has units of \(1/s^{-1}\). Thus, the impulse response is just the solution to the first-order differential equation and can be written as: $$ h(x,t) = e^{-rt} \cdot \delta(x,t)$$
• Diffusion
Diffusion of the molecule is an important process that needs to be considered, since the time scales in this problem can be long. Because the radius of the blood vessels is small, diffusion in the radial direction can be assumed to be quick, and we are only left to model the diffusion in the axial direction. This is governed by Fick's Laws and can be written [2] as: $$ h(x,t) = \frac{1}{\sqrt{4 \pi t}} e^{-x^2/4t} $$

Simulations

Prior Research

References

Feedback