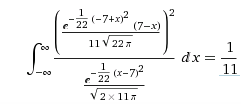
So the score for \(n\) measurements is \(n/\sigma^2\), and we meet the bound exactly.
i) We observe that not only is \(H(p)\) continuous but it is differentiable. $$\frac{dH}{dp_j} = -\sum^X_{i\neq j} 0 - p_j \frac{1}{p_j} - \log{p_j} = -1 - \log{p_j} $$ ii) Every term in the sum that defines \(H\) must independently be non-positive, because \(0 \le p_i \le 1\), so the sum is always non-positve, and \(H\) therefore is non-negative. If \(p_1 = 1\), then \(p_i = 0\) for all other \(i\) and and we see that \(H\) evaluates to zero. Likewise, if \(H\) evaluates to zero, we know, all \(p_i\) must be equal to 0 or 1, but since the sum of all \(p_1\) is 1, there can be only one non-zero term.
iii) We prove by contradiction. Suppose the maximal entropy distribution exists and includes non-uniform probabilities \(p_1\) and \(p_2\) with \(p_1 < p_2\) WLOG. We will show that we can get a higher entropy by slightly increasing \(p_1\) and slightly decreasing \(p_2\). The entropy of the two original terms is $$-p_1 \log{p_1} - p_2 \log{p_2}$$ The entropy of the modified terms is (using the taylor expansion for \(\log{(p+\epsilon)} \approx \log(p) + \frac{\epsilon}{p} \): $$-p_1 \log{p_1} - p_2 \log{p_2} - \epsilon - \epsilon \log{p_1} - \frac{\epsilon^2}{p_1} + \epsilon + \epsilon \log{p_1} - \frac{\epsilon^2}{p_1}$$ Ignoring the second order terms, the change in entropy is $$\epsilon \log{p_2} - \epsilon \log{p_1} = \epsilon \log{p_2 / p_1} > 0 $$ The last expression is greater than zero because we assumed \(p_2 > p_1\). Thus, the entropy takes its maximum when the probabilities are equally distributed, and that value turns out to be \(\log{X}\).
iv) If the drawings are independent, then the chance of seeing \( (x,y) \) is \( p_x q_y \), or the product of the probabilities of seeing each of them separately, and the entropy of joint distribution can be written as $$H(p,q) = -\sum_i^X \sum_j^Y {p_i q_j \log(p_i q_j)}$$ $$= -\sum_i^X {p_i \sum_j^Y{ q_j \log(p_i q_j)}}$$ $$= -\sum_i^X {p_i \sum_j^Y{ q_j \log{p_i} + q_j \log{q_j}}}$$ $$= -\sum_i^X {p_i (\log{p_i} + H(q))}$$ $$= {H(p) + H(q)}$$ Where we have used the fact that probabilities sum to 1.
4.2) We know that \(H(x,y) = H(x|y) + H(y) = H(y|x) + H(x)\), so the second and third equalities follow by substitution. The last equality follows when we write $$ H(x) = -\sum_i^X {p_i \log{p_i}} = -\sum_j^Y \sum_i^X {p_{j|i} p_i \log{p_i}} = -\sum_j^Y \sum_i^X {p(i,j) \log{p_i}} $$ Similarly, $$ H(y) = -\sum_j^Y \sum_i^X {p(i,j) \log{p_j}} $$ Substituting, we get the last relation.
4.3 a) Either all three can be incorrect, or 2 out of the 3 can be incorrect: \( p_1 = \epsilon^3 + 3 \epsilon^2 (1-\epsilon) \)
4.3 b) From (a), \( p_2 = p_1^3 + 3 p_1^2 (1-p_1) \)
4.3 c) We can recursively define \( p_{N+1} = p_{N}^3 + 3 * p_N^2 (1 - p_N)\) with the base cases above. The probability of an error is \(p_N\) while the number of bits required is \(3^N\). It seems that the dominant term for small error rates is \( \epsilon^{2^N} \).
4.4) From (4.20), we can easily calculate the differential entropy of a Gaussian process as: $$ \ln{\sqrt{2 \pi \sigma^2_N}} + \frac{\sigma_N^2 + \mu_N^2 - 2 \mu_N^2 + \mu^2_N }{2 \sigma_N^2} = \frac{1}{2} + \ln{\sqrt{2 \pi \sigma^2_N}} $$ Where \( \mu_N \) and \( \sigma_N \) are the mean and variance of the distribution respectively.
4.5 a) The carrier capacity is: 3300 Hz * log(1+100) = 21.9 kilobits/second.
4.5 b) For the capacity to be 1 Gbit/s, the SNR would have to be about 10000 dB.
4.6) The expected value of \(x_i\) is \(x_0\) so the average of \(n\) measurments is clearly unbiased. The variance of the average is \(\sigma^2/n\), due to the well-known properties of the Gaussian. Does this meet the lower bound?
From Wolfram Alpha, we can do the integral, where the mean is 7 and variance 11 for computational purposes. It turns out that the Fisher score for one measurement is \(1/\sigma^2\)
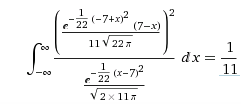
So the score for \(n\) measurements is \(n/\sigma^2\), and we meet the bound exactly.