In [1]:
from numpy import *
%pylab inline

Populating the interactive namespace from numpy and matplotlib

8.1

In [11]:
import sympy as s
from sympy.abc import theta
r, mu, i, d, k, eps, w = s.symbols('r \mu_0 I_0 d k \epsilon_0 \omega')
s.init_printing()
A_r = mu*i*d*s.exp(-s.I*k*r)/(4*s.pi*r)*s.cos(theta)
A_th = -mu*i*d*s.exp(-s.I*k*r)/(4*s.pi*r)*s.sin(theta)
dA_rdr = s.diff( (r*r)*A_r, r)
dA_thdth = s.diff( A_th*s.sin(theta), theta)
div_A = s.simplify((1/r**2)*dA_rdr + 1/(r*s.sin(theta))*dA_thdth)
print "div A = ",
div_A

div A =
Out[11]:
$$- \frac{I_{0} \mu_0 d}{4 \pi r^{2}} \left(i k r + 1\right) e^{- i k r} \cos{\left (\theta \right )}$$ 


















In [12]:



    


grad_r_div_A = s.diff(div_A,r)
grad_th_div_A = s.diff(div_A,theta)/r
res_r = s.simplify(1/(s.I * w * mu * eps) * grad_r_div_A - s.I * w * A_r)
res_th = s.simplify(1/(s.I * w * mu * eps) * grad_th_div_A - s.I * w * A_th)

















In [13]:



    


res_th

















Out[13]:





$$\frac{I_{0} d e^{- i k r} \sin{\left (\theta \right )}}{4 \pi \epsilon_0 \omega r^{3}} \left(i \epsilon_0 \mu_0 \omega^{2} r^{2} + k r - i\right)$$


















In [14]:



    


res_r

















Out[14]:





$$\frac{i I_{0} d \cos{\left (\theta \right )}}{4 \pi \epsilon_0 \omega r^{3}} \left(- \epsilon_0 \mu_0 \omega^{2} r^{2} + k^{2} r^{2} - 2 i k r - 2\right) e^{- i k r}$$











































8.2













In [10]:



    


def poynting_mag(W,r):
    return W/(4*pi*r**2)
def peak_E(W,r):
    return sqrt(poynting_mag(W,r)*377)

















In [15]:



    


print "Magnitude of poynting vector: %.2e J/m^2"%poynting_mag(1e3,1e3)
print "Peak E field: %.2e V/m"%peak_E(1e3,1e3)





















Magnitude of poynting vector: 7.96e-05 J/m^2
Peak E field: 1.73e-01 V/m

























8.3



















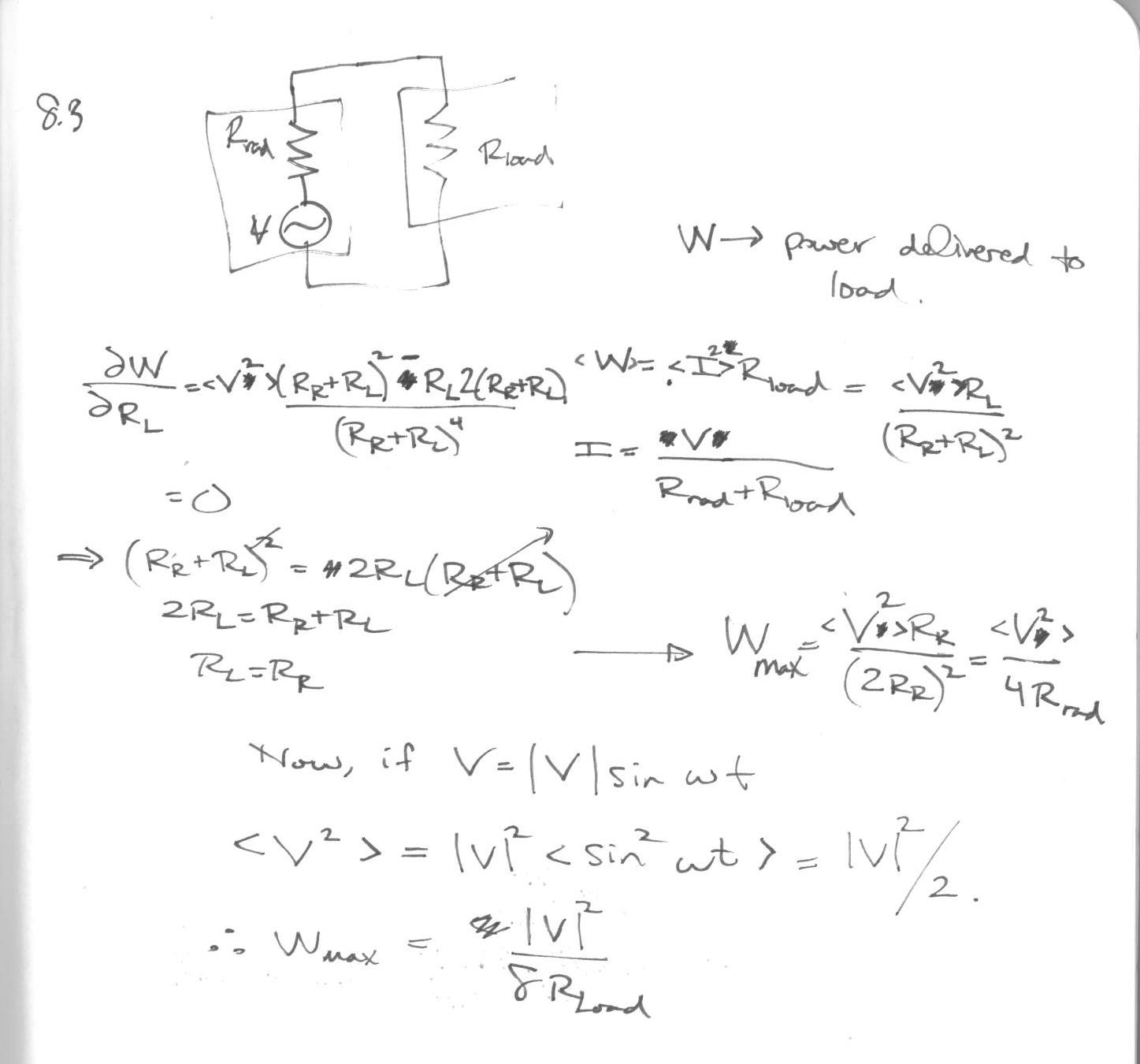
8.4













In [ ]: