Project 10 - Machine Design

Things I learned

• Wow! We can literally make anything! It's really hard to make a whole machine though, and it takes a lot of time.
• How to do math for a real thing. That trig I learned is indeed useful, as it turns out.
• There's so much to learn in the software world! The stuff Ben was able to do this week was really cool, and I'm just discovering all that I can do!

The Process + Pics

1. Group project

Our project for this week was to, as a section, produce a CNC machine of some form. After a brainstorming meeting, we decided on making a Delta Picker . I was on the software team, led by Ben . The project is well documented here , so I won't bother reinventing the wheel and describing all parts of it. Instead, I'll focus on how I specifically helped reinvent a delta picker.

But here's a picture of what we ended up making!

2. The Software

For hardware, we were given a Synthetos TinyG CNC controller, and according to Ben, no one has really done what we were trying to do with the TinyG. His plan, as documented on his Machine Design project page, was this:

• Take in a toolpath expressed as SVG.
• Extract toolpath points from the SVG and translate them from world space (mm) to rail space (mm) in tiny increments.
• Convert the rail-space toolpath points to Gcode and push them to the TinyG for execution.
The functions that we had to write in Python were like so (also described by Ben):
• World2MachineCoords([x, y, z]): given coordinates (x, y, z) in world space, convert it into coordinates (a, b, c) in stepper motor space.
• SVG2Toolpath(svg_file): given a SVG file describing a series of 2D shapes to sketch on the machining plane, convert it into an array of (fairly densely packed) points describing in world space a toolhead motion on both the machining plane and an elevated traversal plane.
• Toolpath2GCode(toolpath): given the array output from SVG2Toolpath(), convert it into an array of literal gcode commands (e.g. G1 F60 X50 Y50 Z50).
• RunJob(svg_file, serial_port): given path to an SVG file describing a series of 2D shapes to sketch on the machining plane, and path to a serial port, send the necessary gcode (and local user interaction) to configure the TinyG for our machine, home the machine, run the machining job, and move the machine out of the way afterwards.

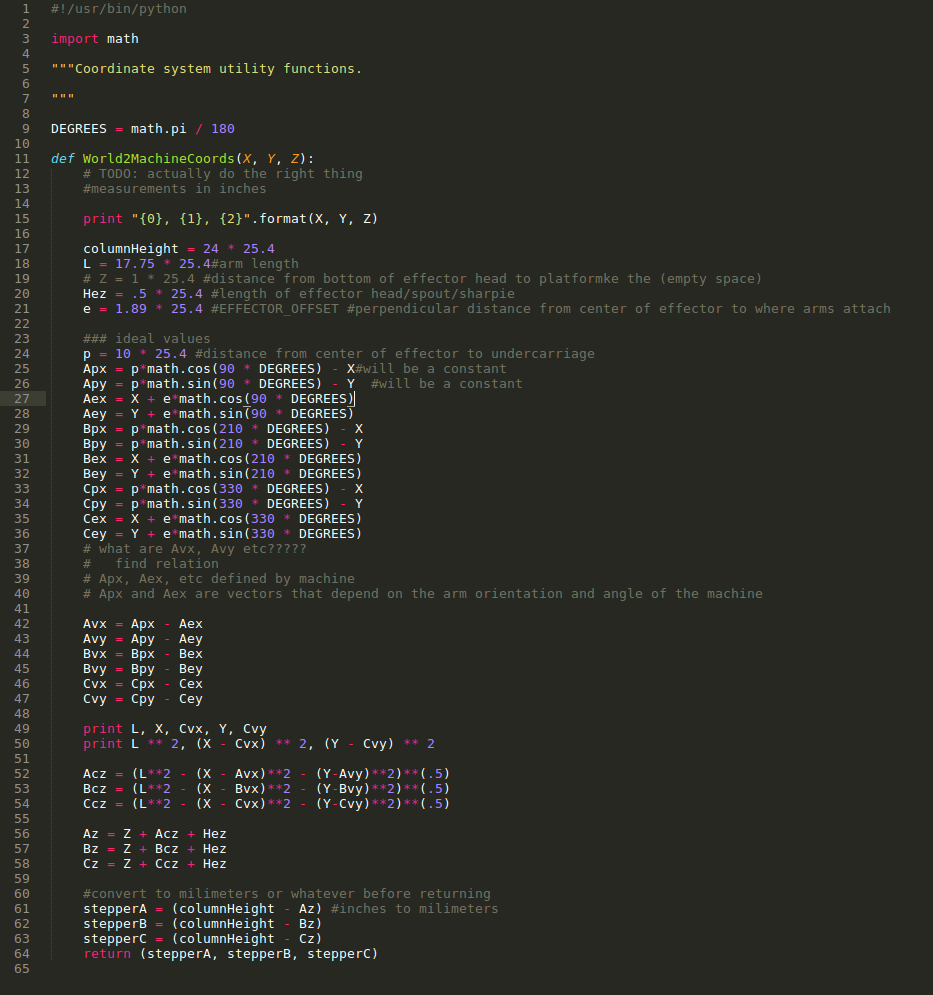
I decided to work on the World2MachineCoords.

3. My code

So basically, the Delta Picker will have three motors that each move up and down a vertical post. The positions of these motors will determine where on the X-Y-Z plane the end effector is. My job is to figure out what these postions are, based on where we want the end effector to go.

This report was really useful in guiding me in my calculations. I spent longer than necessary reading it, because I wanted to make sure I understood the calculations being made; primarily for my own desire to learn, and secondarily to be able to adjust the code if it needed modification.

First, I familiarized myself with the different parts of the diagram that Steve Graves has in the document. Then I started applying the trig that I learned in high school (who knew it would actually be helpful!). Here's a visualiztion that helped me a lot along the way:



Doing inverse kinematics was really fun.

I learned the mechanics of the machine and the math for taking in world coordinates and calculating the positions of the motors. However, there were two variables that I was trying to figure out how to get in the most simple way possible.

It was difficult because we didn't have the actual measurements of the machine, and the ones we did have often kept changing. I used approximations for the majority of the time I spent on the code. When Ben and I were debugging, however, we got a lot of errors - such as the square root of negative numbers! We figured out it was because we had chosen dimensions for the machine that weren't actually feasible. Subsequently, we chose better numbers. Later, I switched to the real, precise measurements at the very end, when everything was actually done.

Here's my final code: