I obtained my source images from the photo sharing website flickr.com. Users upload photos, often taken with a camera-phone, and tag them according to their content. One very popular tag is "squaredcircle", used for images that consist of a circular object filling the frame. I searched for images tagged with both "squaredcircle" and "fruit". From these I selected 16 images of uncut fruit, and 16 images of cut fruit.
Note that there is no correspondence between the uncut and cut fruit, just 16 random images for each. The two datasets are analyzed separately.
I wanted to work in a color space that could handle linear combinations well, without producing inverted colors as often as not. I made up a spherical color space in which the azimuthal angle is half of the hue degree, the polar angle is color saturation, and the radius is the brightness.
This is shown below as a cut-away of a sphere:
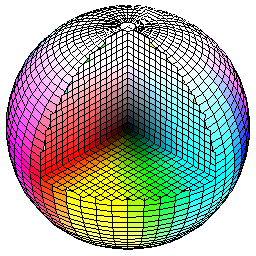
In this space, taking the opposite of a vector doesn't change the color it represents, and adding two colors produces a color in between.
Here are the "top 5" eigenfruit, the principle components, uncut and cut. Interestingly, the colors are similar, even though there was no relationship between the sets of fruit.
We can create new fruit by combining the eigenfruit. I combined the top 4 eigenfruit of each set using random, normally distributed weights, and generated the results below.
We can combine the eigenfruit to yield approximations of the original fruit. Using just combinations of the top 5 eigenfruit, here are the reconstructions, with the original images on the left.
David Greenspan 2005