Introduction
The time it takes a SAT solver to solve a boolean formula is dependent on a number of factors. These include, but are not limited to, the size of the formula, the clausal density of the formula, the size of the formula's unsatisfiable core, and of course, the particular solving algorithm employed. The purpose of this project is to investigate how well a function can be fit to the duration of the solving algorithm based on these features.
To accomplish this, I have gathered extensive performance data for the BerkMin SAT solver against randomly generated formulas and employed Kernel methods to fit functions to it. I will examine how close these functions fit the behavior of random formulas, as well as their ability to fit the behavior of formulas generated more systematically.
Background
A boolean formula consists of boolean variables, the logical operators AND (conjunction), OR (disjunction), and NOT (negation), and parentheses. Given a boolean formula, boolean satisifiability (SAT) is the problem of determining an assignment to the boolean variables for which the formula evaluates to true or determining that no such satisfying assignment exists.
In complexity theory, this problem is known to be NP-complete, and thus in the worst case, very hard to solve. Nevertheless, much progress has been made in engineering efficient SAT solvers. SAT solvers such as BerkMin [1] and ZChaff [2], now exist that make use of clever heuristics to solve most satisfiability problems quickly.
SAT solvers typically operate on boolean formulas in conjunctive normal form (CNF). A boolean formula in CNF is a conjunction of clauses, where each clause is a disjunction of literals, and each literal is either a boolean variable or a negated boolean variable. Special classes of CNFs, known as k-SAT or k-CNF formulas, have a fixed k number of literals in each clause, where no two literals in any clause are identical or the negation of one another. 3-SAT, for instance, refers to the class of CNFs with exactly three literals in each clause.
Prior research has identified phase transitions in SAT problems [3]. Namely, for a fixed k there exists a critical clausal density (ratio of clauses to variables) for which k-SAT problems quickly shift from being mostly satisfiable to mostly unsatisfiable. That is, CNFs with clausal densities much less than the phase transition are almost always satisfiable, and those with densities much greater than the critical density are almost always unsatisfiable. The phase transition for 2-SAT has been proven to be exactly 1, and for 3-SAT is has been estimated to be about 4.3.
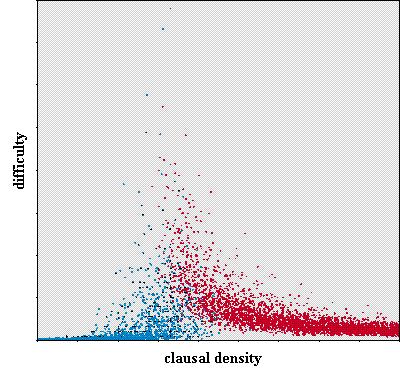
Figure 1. Difficulty and satisfiability versus clausal density [4].
blue are satisifiable; red are unsatisfiable
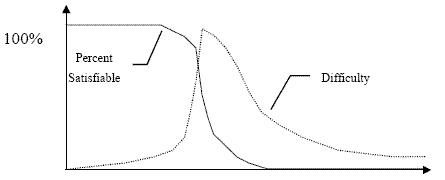
Figure 2. Percentage satisfiable and average difficulty versus clausal density [3].
As indicated in the figures, this phase transition is also correlated with the difficulty of the problem. Problems far from the phase transition tend to be easy to solve (require few decisions by a SAT solver), and those close to the transition tend to be difficult to solve (require many decisions). This makes intuitive sense: most formulas with low clausal densities are very underconstrained are easily satisifiable, while most with high clausal densities are very overconstrained and readily unsatisifiable.
However, the clausal density is not a perfect indicator of the difficulty of the boolean formula. Indeed, as the figures show, there are CNFs relatively far from the phase transition that are still hard to solve and ones close to the transition that are easily solved. For this reason, the difficulty curve in Figure 2 is not a tight fit to the data in Figure 1.
In this project, I will plot and fit a function to the difficulty of unsatisfiable formulas against the clausal density of the formula and an additional variable: an estimate of the size of the minimal unsatisfiable core of the formula. An unsatisifable core of a CNF is a subset of the CNFs clauses that is also unsatisfiable. I will use the iterative technique offered by Zhang and Malik for extracting a small, though not always minimal, core [5]. The ability to identify unsatisfiable cores has proven useful in many applications, including debugging over constrained declarative models [6].
I expect the size of the core and the clausal density to provide a much better indication of the difficulty of an unsatisfiable formula than the clausal density alone. If a formula has a small unsatisfiable core, then the solver will need to visit few clauses before finding the formula unsatisfiable; conversely, if the core is large, the solver will have to visit many clauses to make the determination.
To clarify, fitting a function to this data will not be of use in determining the difficulty of a formula prior to solving it. This is because the process of finding the unsatisifiable core of a formula requires first requires solving it. In fact, it requires executing the solver several times in successesion. However, the function fit could be very useful for the opposite: estimating the size of the core given the difficulty of solving it. Because of the long duration of the core extraction process for large boolean formulas, it may be advantangeous to approximate its size instead of extracting it directly. At the least, it should provide greater insight into the nature of boolean formulas and the behavior of SAT solvers.
Having fit a function to the data, I will test this function's predictive capability no some SAT formulas that are not randomly generated. This should help answer the question about whether data gathered from randomly generated SAT formulas tells us anything about SAT formulas that are constructed more systematically in practice.
Results
I randomly generated 2550 unsatisfiable 3-SAT formulas. Here are two scatter plots of a subset of the data involving only those formulas with exactly 1000 or 1500 clauses. The first (Figure 3) plots the time it took to solve the formula against the density of the formula, and the second plots the time against the percentage of the formulas clauses that were in the unsatisfiable core.
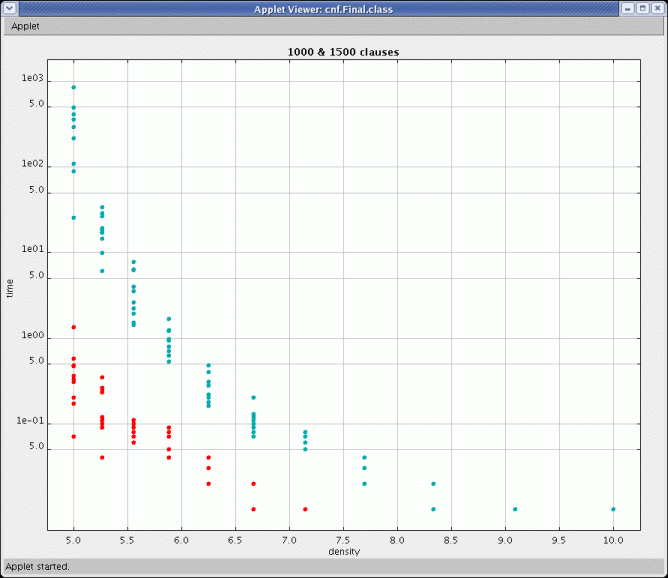
Figure 3. Time to solve versus density of SAT formula.
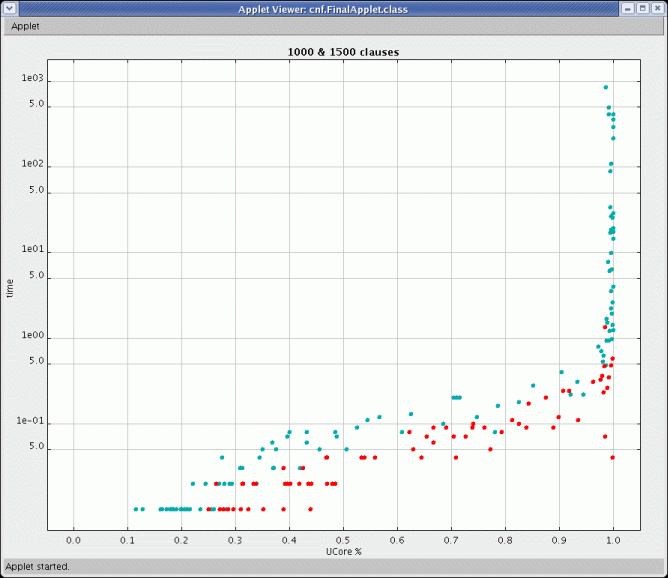
Figure 4. Time to solve versus percentage of clauses in the unsatisfiable core of SAT formula.
To measure how well the function fit the data, I calculated the average squared difference between the actual and predicted values:
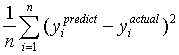
The initial results did not look promising. This averaged squared difference was extremely large. However, eyeballing some of the data showed the largest outliers to be when the unsatisfiable core was the entirety of the formula. So I repeated the regression this time only using the formulas whose unsatisfiable core was a strict subset of the clauses. A comparison of the average squared difference for different sets of features and the two sets of formulas is shown in Table 1.
| features | all formulas | unsat core < clauses |
| clauses | 890,000 | 730,000 |
| vars | 580,000 | 370,000 |
| unsat core | 340,000 | 160,000 |
| clauses, vars | 290,000 | 8,500 |
| clauses, vars, unsat core | 80,000 | 7,500 |
Table 1. Average squared difference between real and predicted times.
Clearly, if we were to leave out those formulas with an unsat core 1 clause smaller than the entire formula, the curve would fit the data even tighter. The natural observation is that difficulty of SAT formulas (at least when solved with BerkMin) are still extremely volatile even when the size and unsatisfiable core of the formulas are fixed and especially so at the phase transition. While the size of the unsatisfiable core does give some of the reason, it certainly doesn't tell the whole story.
As stated in the "Background" section, fitting a curve that uses the unsatisfiable core as a feature would be of no practical use in predicting the time, because finding the core requires running the SAT solver several times anyway. However, the curve could be of use in estimating the size of the core given the time the formula took to solve. Such an experiment would also test the ability of data gathered from randomly generated formulas to predict the behavior of non-randomly generated formulas.
To conduct this experiment, I first performed the regression over again, this time using the time as a feature and the size of the core as a value. I then took 10 CNF formulas generated by The Alloy Analyzer constraint solver and converted them into 3-SAT. Given the number of variables, clauses, and the time it took to solve, I predicted the percentage of clauses in the unsatisfiable core and compared this to the actual values. The results are shown in Table 2.
| CNF # | Actual | Predicted |
| 1 | 6.69% | 51.15% |
| 2 | 22.11% | 24.94% |
| 3 | 4.28% | 26.53% |
| 4 | 1.56% | 0.21% |
| 5 | 10.30% | 0.01% |
| 6 | 8.31% | 0.00% |
| 7 | 16.01% | 0.00% |
| 8 | 13.65% | 46.58% |
| 9 | 14.93% | 0.00% |
| 10 | 12.92% | 0.11% |
Table 2. Predicted vs Actual Percentage of Clauses in Unsat Core.
As the table show, the representer function generated by the regression has poor predictive capability. This demonstrates the sheer volatility in the difficulty of SAT formulas. Hopefully future students and researchers can try to explore more function fitting to satisfiability formulas and eventually achieve a tighter fit.
References:
[1] E. Goldberg and Y. Novikov. "BerkMin: a Fast and Robust SAT Solver". Design, Automation and Test in Europe Conference and Exhibition (DATE'02). 2002.
[2] M. Moskewicz, C. Madigan, Y. Zhao, L. Zhang, and S. Malik. "Chaff: Engineering an Efficient SAT Solver". Proceedings of the 38th Design Automation Conference (DAC'01). 2001.
[3] K. Xu and W. Li. "The SAT Phase Transition". Science in China (Series E), Vol. 42, No. 5, p494-501. 1999.
[4] T Walsh. "Phase Transition Behavior". http://www.cs.york.ac.uk/~tw/phase.ppt.
[5] L. Zhang and S. Malik. "Extracting Small Unsatisfiable Cores from Unsatisfiable Boolean Formulas". Submitted to Sixth International Conference on Theory and Applications of Satisfiability Testing (SAT2003). 2003.
[6] I. Shlyakhter, R. Seater, D. Jackson, M. Sridharan, M. Taghdiri. "Debugging Overconstrained Declarative Models Using Unsatisfiable Cores". 18th IEEE International Conference on Automated Software Engineering (ASE 2003). October 2003.