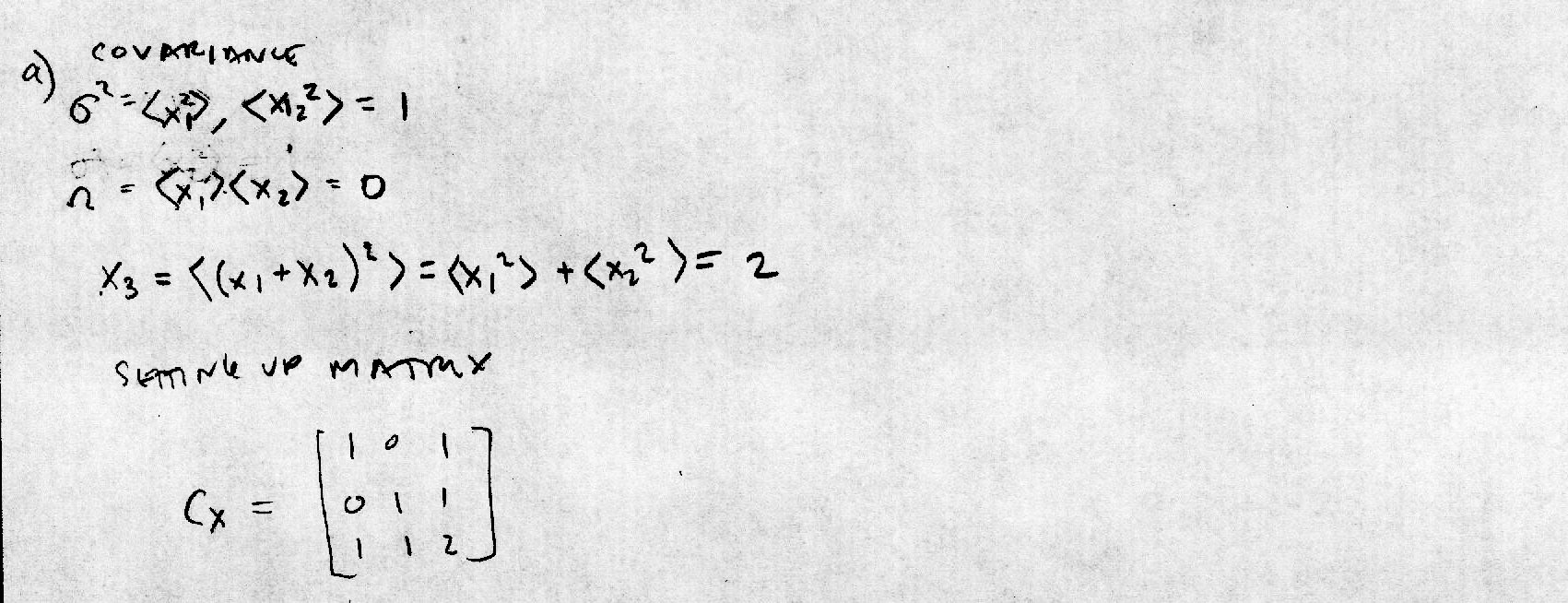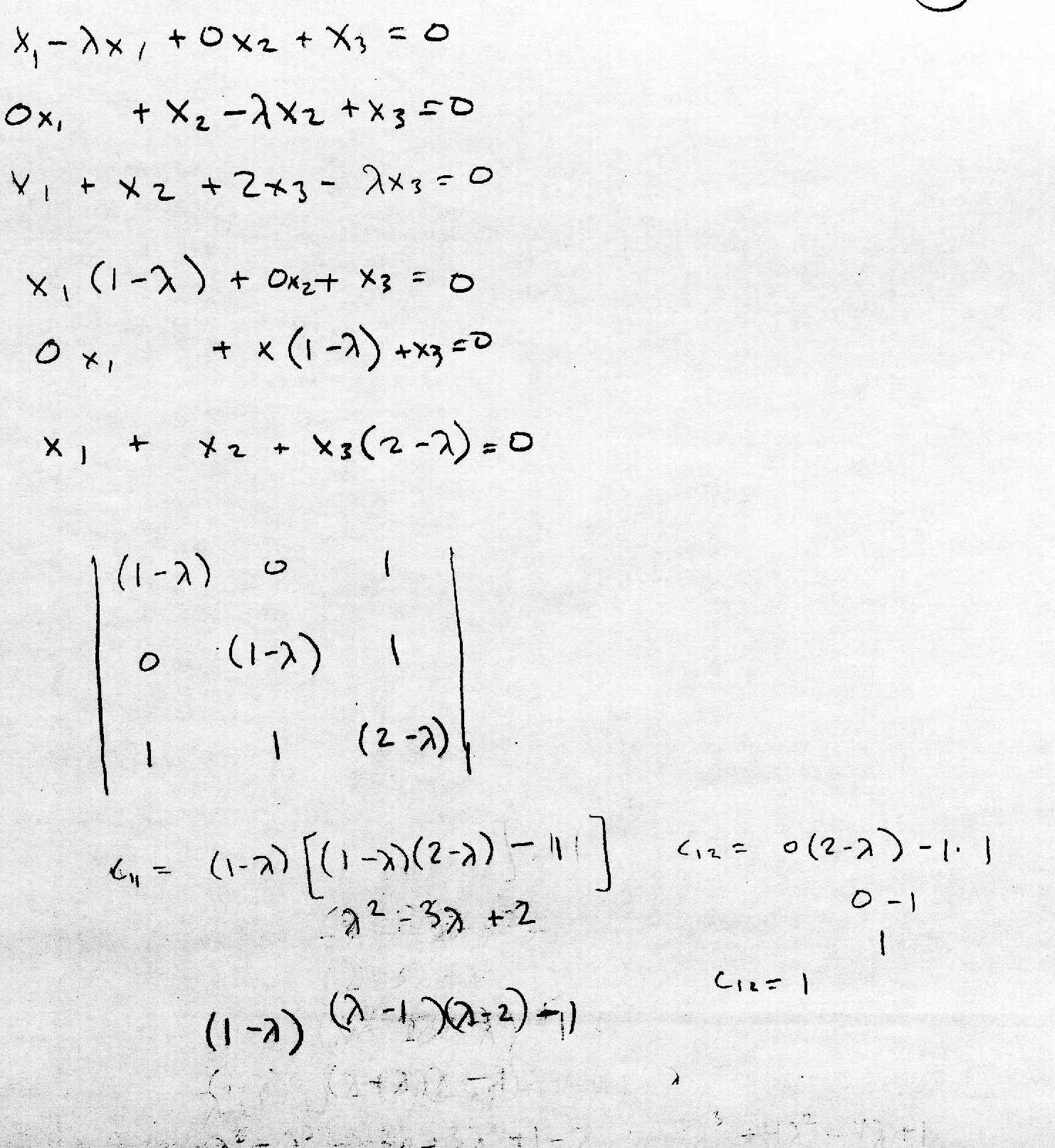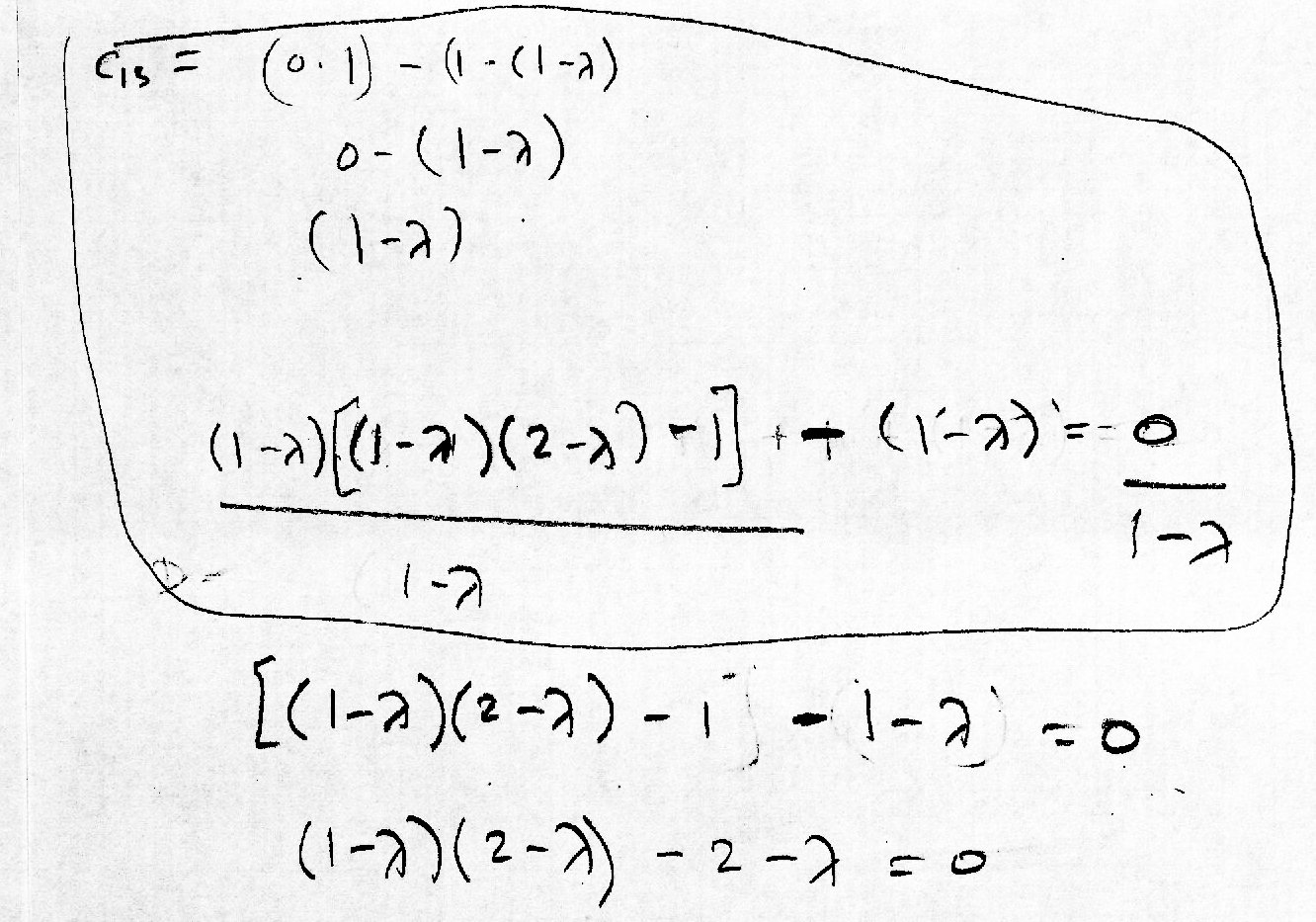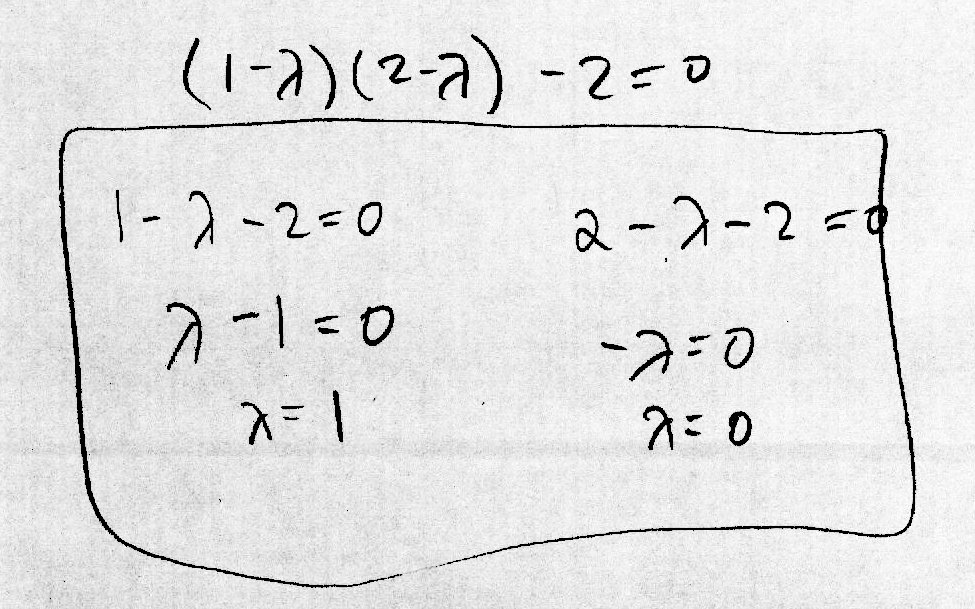Calculate the inverse wavelet transform, using Daubechies fourth-order coefficients, of a vector of length 2^12, with a 1 in the 5th and 30th places and zeros elsewhere.

My solution in python: daubTest3.py

(a) Analytically calculate the covariance matrix of a three-component vector x.

First, I set up the vectors with zero mean and unit variance and then form the covariance matrix:

(b) What are the eigenvalues?

Solving the eigenvalues that satisfy the equation of a square matrix times the eigenvector and a scalar:

Rearranging the equation in preparation to solve the determinant of the coefficient matrix:

There are three scalar values, which means that there are three eigenvalues of the original matrix:

The eigenvalues are 1, 0, and 3:

(c) Numerically verify these results by drawing a data set from the distribution and computing
the covariance matrix and eigenvalues. (d) Numerically find the the eigenvectors of the covariance matrix
with no zero eigenvalues. Verify this on the data set.

Values of vector x:

Covariance of x:

Eigenvalues of x:

Source code: num-cov.py