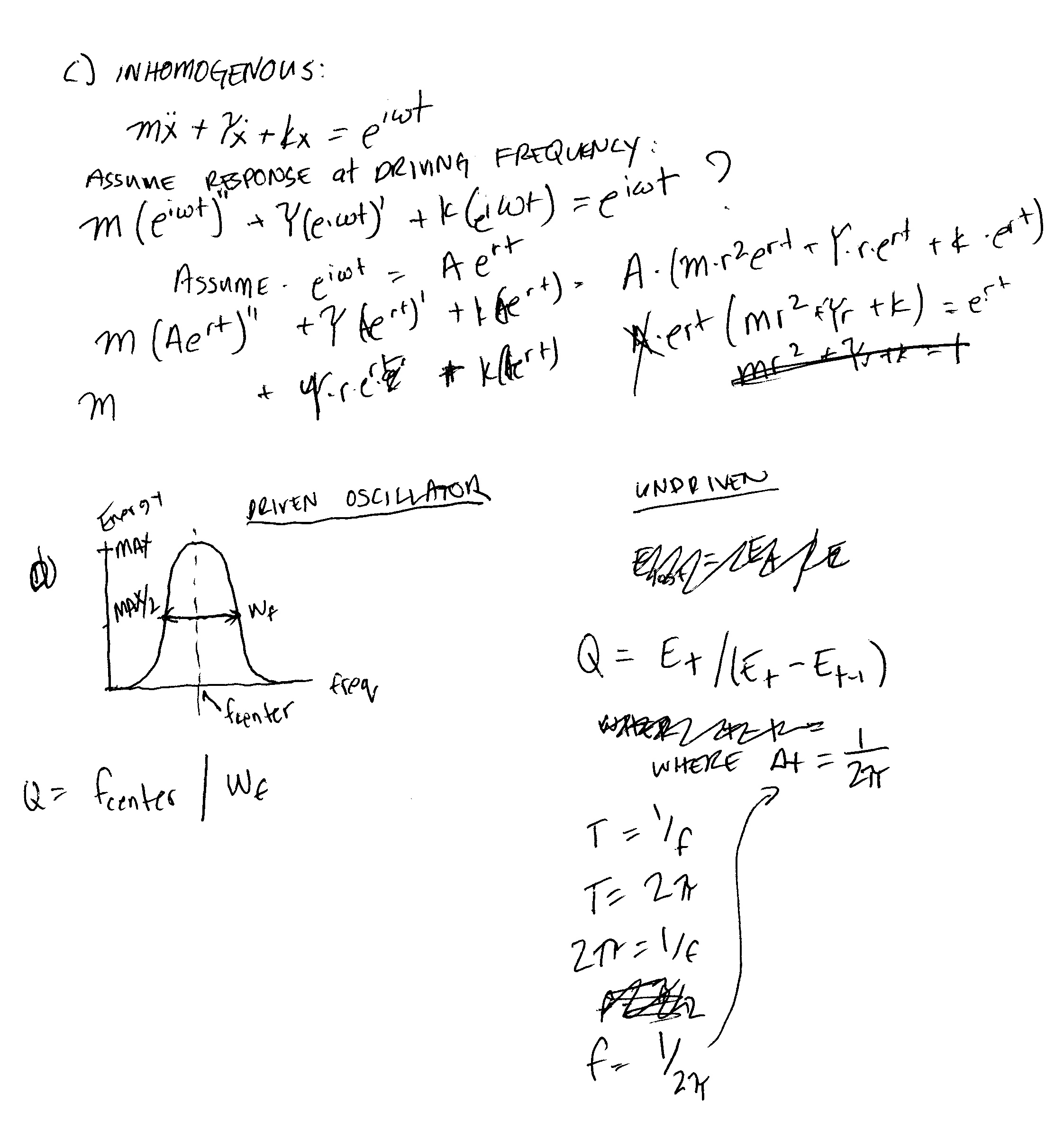
Homework: Ordinary Differential and Difference Equations

a) Under what conditions is this simple harmonic motion?
When γ, i.e. friction, is 0 this becomes simple harmonic motion.
b) Comment on the possible cases. How does the amplitude depend on the frequency?
When γ approaches infinity, this is the case of infinite friction. γ overpowers the other terms under the square root and the division falls away and we get two solutions. In the lefthand expression we end up with -γ + γ, which is 0. This makes sense: under infinite friction there'd be no motion. The solution of the right expression ends up with -2γ which falls to negative infinity. This doesn't have any meaningful physical interpretation and is a degenerate case.
When there's no friction, γ = 0. Both solutions end up as complex linear combinations of k and m: +/-(i*sqrt(m)*sqrt(k))/m. This gives the simple harmonic motion situation we saw above with the imaginary portion of this corresponding to ω.
When mass rises to infinity, as the only mass-term outside the square root, the denominator dominates and both solutions become 0. As mass increases, motion reduces towards 0.
When the mass falls towards zero, both solutions assymptotically rise to infinity for the same reason described above. Decreasing mass results in more motion.
Question: I don't understand the portion of this that's about the relationship between the amplitude and the frequency? What is being asked there?