Point Cloud Approximator

Proposal

Having worked extensively with the Kinect for 3D sensing in the past, I've always wanted to build a tool for converting dense point clouds into simplified approximations consisiting of a minimal number of planes and simple solids. Such a tool could be used to capture parametric measurements of spaces and objects that would be incredibly useful in different design processes, particularly game design, vfx prototyping, industrial design, and installation/interior design.

There is significant prior work in this area clustered in two main areas: reverse engineering and level of detail rendering. My contribution will differ from the existing work in that it will focus on the properties of point clouds from common contemporary low-end sensing systems, particularly the Kinect and 123D Catch.

Approach

After surveying the broad body of relevant literature, I decided to implement an approach based on the changing orientation of estimated point normals, largely based on [Castillo and Zhao]. This approach broadly consists of 3 steps: use principal component analysis or total least squares on each point's nearest neighbors to estimate a normal for the point, build an adjacency matrix comparing the angle of each point's estimated normal with all the other points, run connected components over this adjacency matrix to segment the point cloud into a set of distinct faces. My addition to this approach is then to take the computed segments and discard all points interior to each segment, producing a point cloud with a small fraction of the number of points that still captures the shape of each distinct object.

Note: Castillo and Zhao outline an additional noise reduction step where they add a minimization constraint to their total least squares procedure that attempts to reduce orthogonality mismatch in the estimated normals. I skipped this step so that I could use the more straightforward-to-implement vanilla PCA. While this will produce worse segmentation results (especially around gradually curved surfaces) it should be good enough for a proof-of-concept with the possibility of adding aditional noise reduction later.

I chose to use OpenFrameworks as my platform of choice for implementation. I know its ofMesh implementation quite well and knew that it would be a good platform for efficiently storing and comparing normals. Further, the performance (and low-level control ver memory) of C++ is valuable when doing relatively intensive computational tasks on hundreds of thousands of points. Finally, I released two libraries built as part of this project as open source contributions to the OpenFrameworks community: ofxANN, a wrapper for the libANN aproximate nearest neighbor library. And ofxPCA, a PCA implementation based on Eigen, a highly optimized and extremely portable C++ library of linear algebra routines.

The code for this project is available here: atduskgreg/ScanSimplifier as well as in the Nature of Mathematical Modeling class archive here.

Results

I had some limited success segmenting the point cloud based on this technique. However, the noise in the estimated normals required very large point neighborhoods to be considered and the resulting segmentation was so fragmented that it had very limited utility as a simplification technique. I did skip the noise reduction technique described by Castillo and Zhao so future work implementing that could dramatically improve the results.

Final point cloud segmentation acheived:

Literature Survey

Boundary Representations

Volumetric Representations

Functional Representations

Implicit Surfaces

Work Log

Doing initial reading it looks like a segmentation step before fitting may be crucial. A new segmentation method for point cloud data presents a good review of segmentation methods. They're split into: edge-detection methods, region-growing, and hybrid methods. Representative papers for each of these approaches are: Segmented descriptions of 3-D surfaces [Fan et al] and Segmentation and Classification of Range Images [Hoffman and Jain], respectively.

Reading about various segmentation methods, I found that they all depend on normal estimation for an unstructured point cloud. So I began to investigate that problem. I was quickly drawn to Point Cloud Segmentation via Constrained Nonlinear Least Squares Surface Normal Estimates [Castillo and Zhao], which uses PCA on a point's K-nearest neighbors to estimate its normal. ([Mitroy and Nguyen] go into more detail on this technique (apparently referred to as "total least squares"), with particularly good coverage of its sensitivity to noise). [Castillo and Zhao] also then go on to develop a "connected components" segmentation technique that uses variation in the normals to segment the point cloud. This seems like a very promising direction (with the edges of segments then usable as a minimal representation or the seed for further approximation work).

K-Nearest Neighbors and libANN

Started taking some steps towards an implementation of the segmentation technique described in [Castillo and Zhao]. The first order of business is being able to find the k-nearest neighbors for a point as the input to the normal estimation process. I reviewed some work on approaches to knn for point clouds ([Sankaranarayanan, Samet, and Varshney] and various tutorials on using kd-trees for the task) and decided to start by using a library for KNN instead of my own implementation so I could focus on the rest of the normal estimation process. After some additional searching, I landed on ANN, a approximate nearest neighbor search library in C++ (I'm planning on doing this project in OpenFrameworks so a C++ implementation is perfect).

I was able to get ANN compiling on macosx with just one minimal change represented by this diff (applied to ann2fig/ann2fig.cpp):

583c583
< main(int argc, char **argv)
---
> int main(int argc, char **argv)

With ANN compiling, I put together some basic starting code in OF that converted a depth image frome the Kinect into an ofMesh (OF's type for representing 3D point data). The next step is to apply ANN to this ofMesh. (I plan to use ofxKinect, OF's official Kinect interface library, for obtaining point clouds, which provides the depth data as an ofMesh so this code will apply to that cleanly and in the meantime I can work without having to have a Kinect plugged into my machine constantly.)

Spent some significant time working on integrating ANN into OF today. Ran into a problem because ANN is compiled for a 64-bit architecture and OF is currently 32-bit only. Need to find a way to recompile ANN as 32-bits.

Succeeding in compiling ANN for 32-bit architecture by adding "-arch i386" to linker flags in Makefiles where appropritate. Then encountered a strange problem where XCode seemed to refuse to link against c++ until I added libc++.dylib to the "Link with Binary Libraries" list under Build Phases.

Two useful tools I came across in debugging this problem are the "ar" and "file" unix commands. ar can list the object files that are concatenated into a particular .a and also separate them out. file can inspect a particular file and give useful information abotut it. This is how I figured out that ANN had been built for 64-bit architecture and how I was able to tell when I'd corrected the problem:

> ar -t libANN.a 
__.SYMDEF
ANN.o
brute.o
kd_tree.o
kd_util.o
kd_split.o
kd_dump.o
kd_search.o
kd_pr_search.o
kd_fix_rad_search.o
bd_tree.o
bd_search.o
bd_pr_search.o
bd_fix_rad_search.o
perf.o
> ar -xv libANN.a ANN.o
x - ANN.o
> file ANN.o
ANN.o: Mach-O object i386

Meanwhile, in actual code land, I've been working on writing the code to convert OF's vector type into the format that ANN wants for points. ANN's data type, ANNpointArray, is an array of pointers where each pointer refers to an array representing each dimension of a particular point. Conveniently, OF provides a getPtr() method on its ofVec3f class and arranges its data so that the x-, y-, and z-components are adjacent floats. The result is that I'm able to compose the ANNPointArray in the correct structure without having to duplicate any data.

The downside to the above match betweeen ANNPointArray and ofVec3f turned out to be that ofVec3f stores its data as floats and ANN defaults to doubles. The only way to set ANN to use floats for its point data is to recompile it after having altered a typedef in ANN.h. So I did that since floats are the appropriate point type for OF because of how commonly used ofVec3f is.

I got nearest neighbor search working with ANN in OF. I wrapped up my code into the OF addon format so others can use it as well: atduskgreg/ofxANN (this also includes the libANN.a file for the 32-bit build with ANNPoint being set to float type).

Implementing PCA with Eigen

Next, with ANN working, I got started on implementing PCA on the neighbors that were returned by the search so as to approximate the normal. To this end I needed a C++ library for Matrix routines. After some research, I quickly settled on Eigen. Eigen takes the form of a (large) collection of header files meant to be portable across platforms so it was quite easy to integrate. (The one "gotcha" is that the src/ directory that comes inside of the Eigen folder of headers must be present for compilation to work, but not actually included in XCode so that it does not become a compilation target on its own. If XCode does attempt to compile it, an giant pile of non-sensical errors will result.)

Continuing the work of using Eigen to implement PCA. Eigen provides a Map datatype meant to allow the library to work with data that is already present in memory without the need to first copy it. Since I have the input points in the form of a vector of ofVec3fs, getting access to the raw array of floats proved a bit of a challenge. After a bit of poking around I found that in C++11 vector's data() member function returns a pointer to the first element of the vector. And the elements are laid out continuously in memory cf here. And, finally, conveniently, ofVec3f keeps each of its three coordinates adjacently in memory as well. So just casting the vector ponter to pointer to a float (i.e. (float *)myVector.data()) will treat the whole vector as a 1D array of floats, which is just what Map needs.

One more gotcha! Upon inspection, I realized that Eigen was importing my data column major instead of row major, causing all kinds of havoc by breaking up each input point across multiple rows and columns. After reading the Eigen docs a bit more this was easy to solve by using a typedef to create a custom Matrix type that was RowMajor.

After some additional wrestling with Eigen's types, I successfully implemented PCA. Due to Eigen's powerful matrix-level operations (with SIMD acceleration and therefore quite fast!) the core of the implementation just came down to three lines:

MatrixVec3f meanCentered = data.rowwise() - data.colwise().mean();
MatrixVec3f cov = (meanCentered.adjoint() * meanCentered) / double(data.rows());
EigenSolver eig(cov);

I hadn't see the definition of the adjoint for a Matrix before but came across this approach in reading about PCA implementations in Eigen and ended up learning something.

Interestingly, when I first implemented this I was only sampling 5 neighbors around the given point. I found many sets of points of this size all shared an identical z-value, resulting in one of the eigenvectors being (0,0,1) the unit vector in the z-direction with an eigenvalue of 0. Increasing the size of the neighborhood to 7 or 10 eliminate the problem for most points I sampled.

Now the only remaining step is to sort the resulting eigenvectors by the eigenvalues and wrap them up into an appropriate return type.

With that finished, I published the full Eigen-based PCA implemenation as an OF addon here: atduskgreg/ofxPCA.

Benchmarking Eigen PCA

Since this will likely be the slowest part of the process, I benchmarked it at this stage at various numbers of neighbors. Here were the results (where "n" is the number of nearest neighbors considered in the PCA analysis and "pts" is the number of points in the point cloud:

Process the full point cloud:
[n: 5 pts: 307200] time elapsed: 66.2558
[n: 7 pts: 307200] time elapsed: 72.7227
[n: 10 pts: 307200] time elapsed: 76.7598

Skip the points with depth value 0:
[n: 5 pts: 270734] time elapsed: 59.3171
[n: 7 pts: 270734] time elapsed: 66.1146
[n: 10 pts: 270734] time elapsed: 71.6049

Skip every other point as well as those with depth value 0
[n: 5 pts: 135343] time elapsed: 33.0864
[n: 7 pts: 135343] time elapsed: 36.754
[n: 10 pts: 135343] time elapsed: 38.9376

These may seem like long run times, but this code is performing PCA on sets of 10 3-float vectors a few hundred thousand times, so this is not terrible.

In this very non-scientific study, the time scaled approximately linearly with the number of executions of PCA. And the number of neighbors seem to account for only a small portion of the run time. It is definitely PCA that is the slow part of this. Here's what the numbers look like w/o PCA, i.e. with just the nearest neighbor search:

ANN nearest neighbor finding alone:
[n: 5 pts: 270734] time elapsed: 0.843394
[n: 7 pts: 270734] time elapsed: 0.994186
[n: 10 pts: 270734] time elapsed: 1.20518
[n: 50 pts: 270734] time elapsed: 3.3981

I theorize that time spent in PCA could be dramatically reduced if we went through and loaded all of the neighbor sets into a single Eigen matrix and then ran each PCA analysis on the relevant subset of that matrix. Although the trade-off would be the creation of a single very large matrix (~300k vertics * 3 floats per vertex = ~90000 entries) that would need to be loaded all into memory at once. Will try implementing this with Eigen's Block operations.

Interestingly, contrary to my expectations this optimization didn't help significantly at all. Cutting just a second or two off the PCA analysis:

All runs skipping only depth points with value 0:
[n: 5 pts: 270734] time elapsed: 58.8337
[n: 7 pts: 270734] time elapsed: 65.523
[n: 10 pts: 270734] time elapsed: 70.5228

I'll have to leave optimization for another day.

Results of PCA-based Normal Estimation

With the PCA implementation complete I ran it against each point in the point cloud, using their neighbors to calculate a set of eigenvectors. I then selected the eigenvector corresponding to the smallest eigevalue (i.e. the normal most orthogonal to the surface defined by the point and its neighbors) and wrote that into the ofMesh data structure as the point's normal.

I wrote a quick routine to visualize the normals so I could inspect the results. Here's what they look like for one of my main test depth images.

Test image:

Normals:

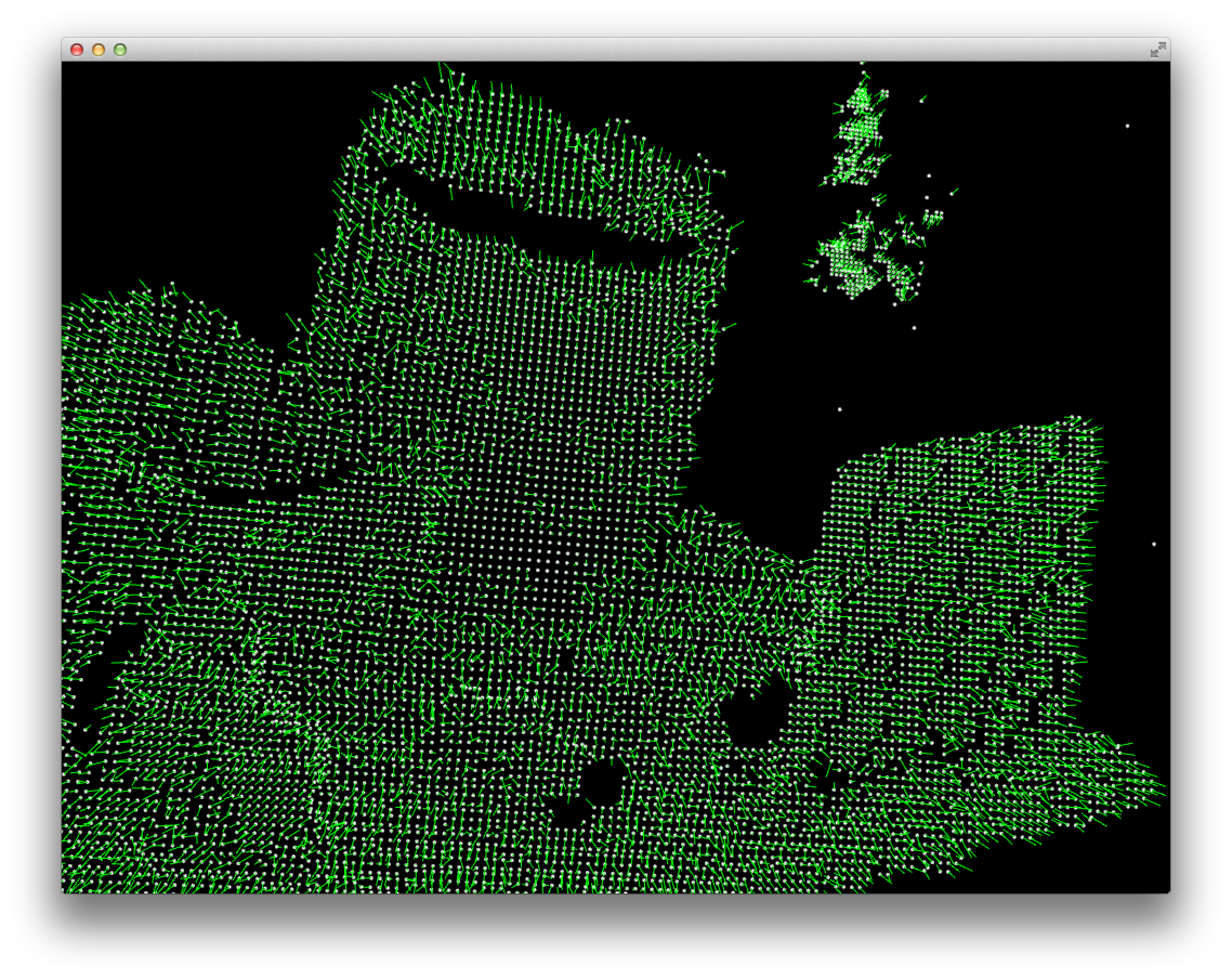
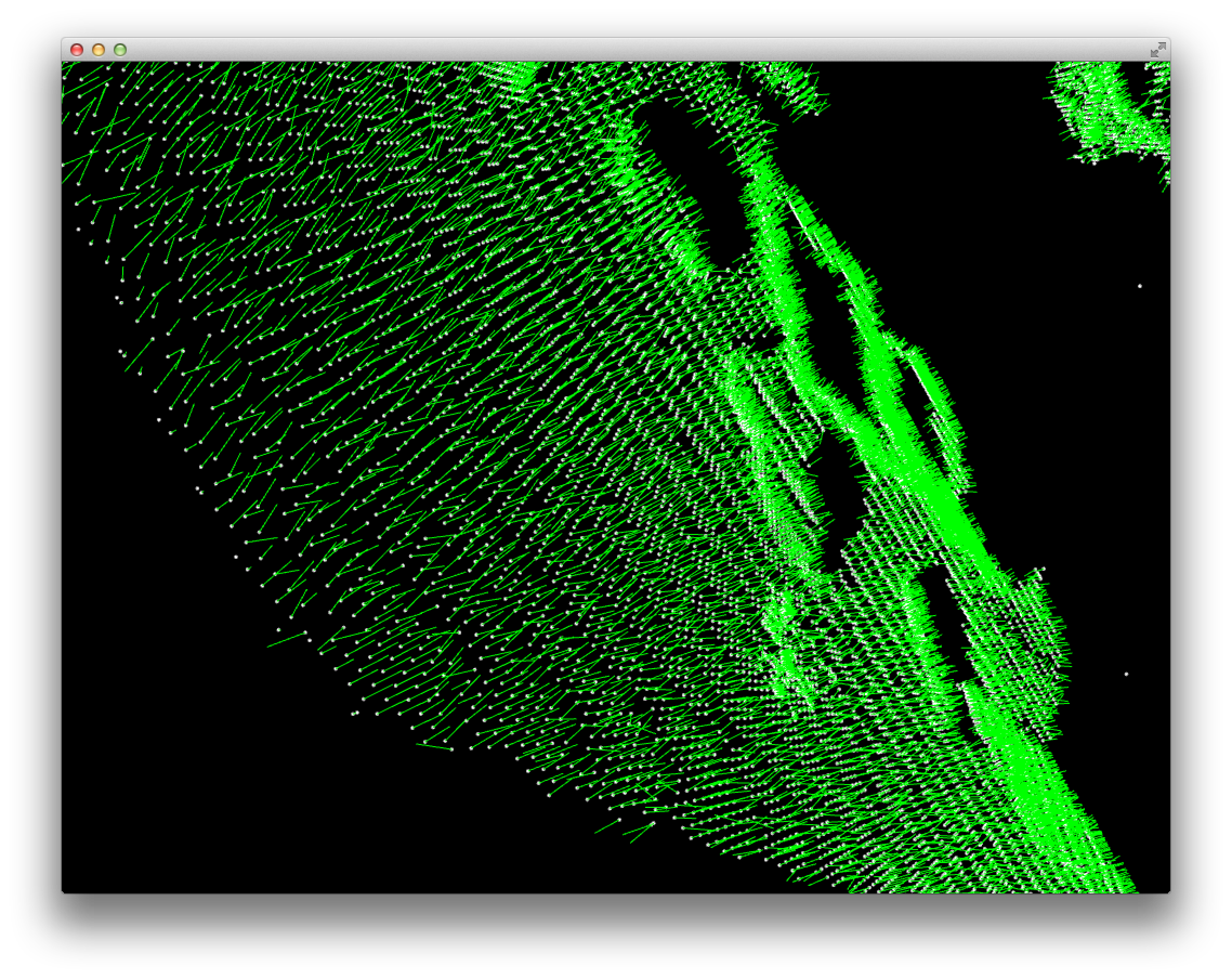
You can see both that the normals are quite noisy and that the do seem to basically point in different directions for different surfaces.

Here's a video fly-through of the visualization that makes it a little easier to see the results:

Scan Simplifier: Estimated Normals from Greg Borenstein on Vimeo.

Noise Reduction: Skip It

The next step presented by [Castillo and Zhao] after this initial normal estimation are refinement stages. They perform a noise reduction step by minimzing the orthogonality mismatch between adjacent normals. These step is posed as a refinement on the Total Least Squares minimization formulation they used for the initial normal estimate. However, since I'm working towards a rough first version, I'll skip noise reduction at this stage and move on towards segmentation.

Segmentation: Constructing the Adjacency Matrix

Catillo and Zhao segment the estimated normals based on their proximity and the variation of their normals. They construct a symmetric adjacency matrix for all of the points. Each entry in this matrix is filled with a 1 or a 0, where 1 indicates that the points lie on the same surface and the 0 that they lie on different surfaces. Points are considered to lie on the same surface if they are neighbors and their normals are within a given angle of each other. They then perform a connected components labeling on the resulting adjacency matrix in order to produce a segmentation. I plan to then perform an additional pass on the segmented point set to eliminate all points that lie in the interior of each segment so that the result will consist of the fewest points necessary to describe the boundaries between objects.

Here's the detailed algorithm I implemented to construct the adjacency matrix: 

initialize an adjacency matrix that is MxM (where M is the total number of points in the point cloud)
for each point in the point cloud
  write a 1 in Aii (the entry representing the point's adjacency with itself)
  look up its normal from the result of our previous PCA calculation
  find its k-nearest neighbors using ANN
  for each neighbor
    look up the neighbor's normal from the PCA calculation
    measure the angle between the point's normal and the neighbor's normal
    if the angle is less than some threshold
      write a 1 in the matrix
    esle
      write a 0 in the matrix

while implementing this I encountered some strange behaviours in Eigen with very large matrices (if we take the full set of non-zero points in the cloud we're talking about a 250000x250000 matrix). The trick to getting Eigen to perform reasonably with large matrices seems to be making sure to use matrix types with dynamic numbers of rows and columns.

Segmentation: Implementing Connected Components

With the adjacency matrix in place, the last step in the segmentation process consists of implementing connected components. There are two options for approaching this problem: depth-first or breadth-first. A depth-first approach would start from a vertex and then recursively examine its neighbors and their neighbors (and so on). A breadth-first strategy loops over each vertex, aggregating all the neighbors that need to be categorized and placing them in a queue before working through that queue. Despite both approaches theoretically being O(n), breadth-first has the advantage of having a bounded memory requirement and not need recursion. So that's what I went with.

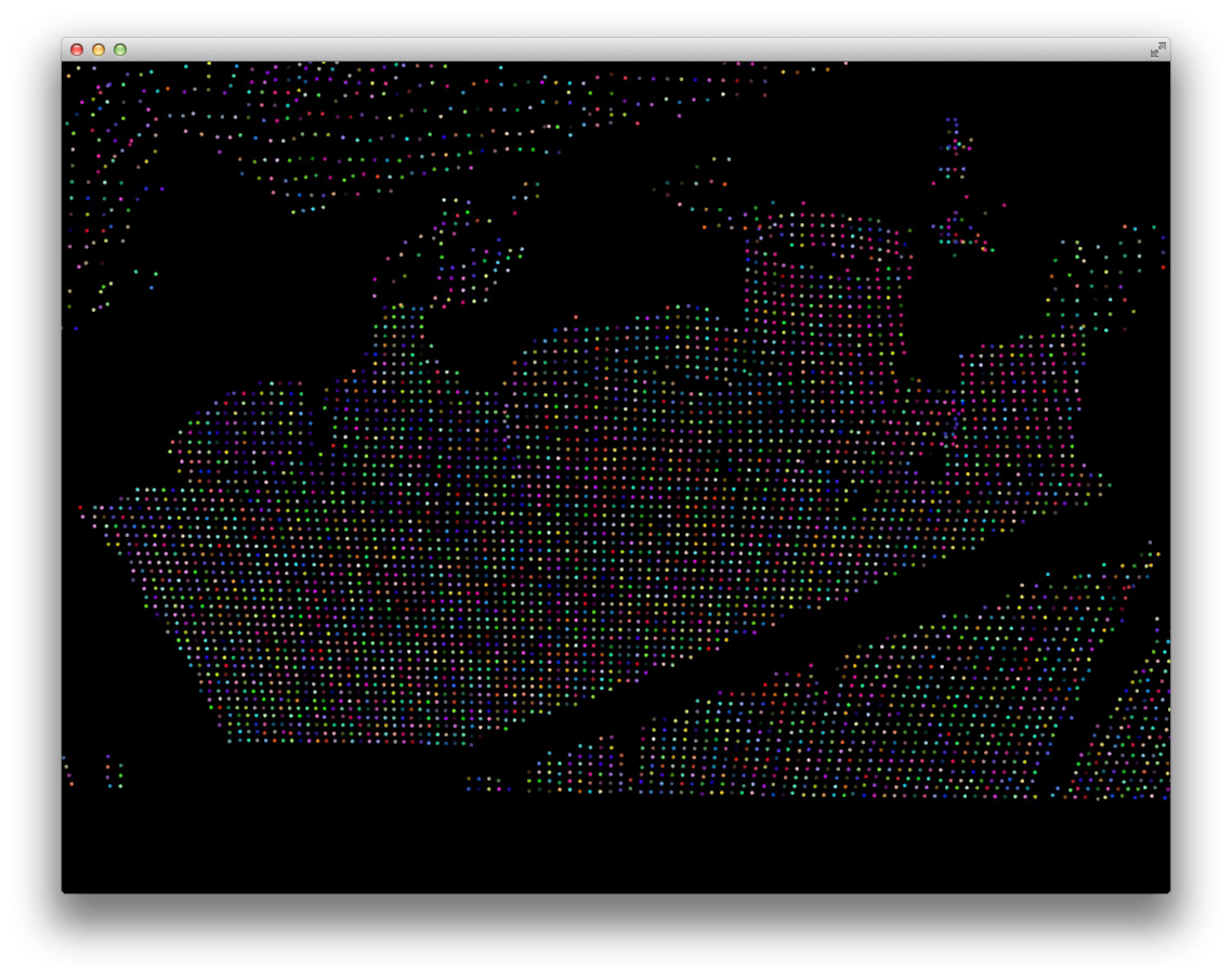
I succesfully implemented connected components using this scheme and displayed the point cloud with each point colored based on its component. The result was a multi-colored fail:

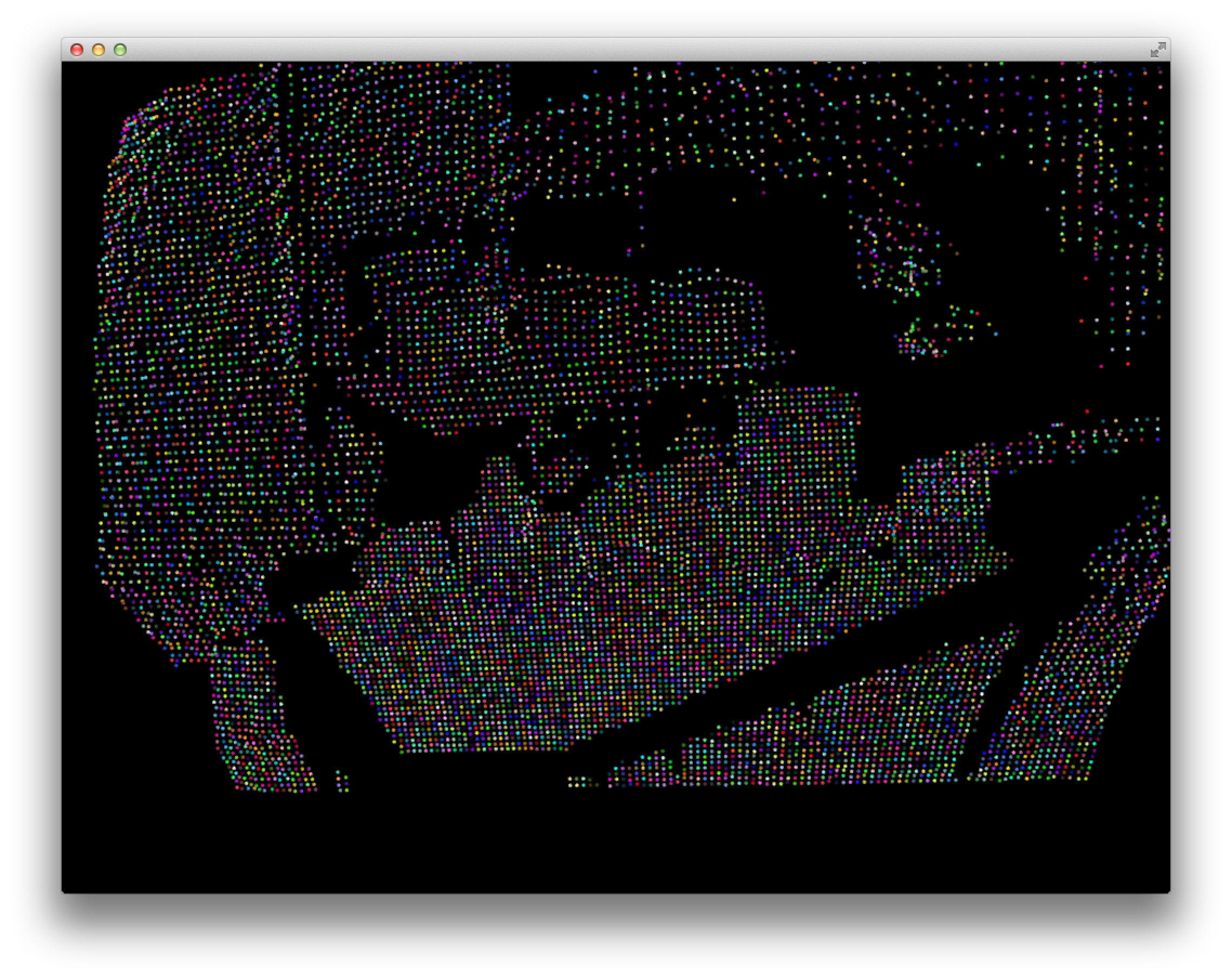
Upon inspection, it turned out that the adjacency matrix is extremely sparse, which results in a ridiculously high number of components: 

num non-zero: 79392/118200384 (0.000671673)
num components: 7356

This remained true even as I loosened the requirements for the angle between neighboring normals to be adjacent (up to 90 degrees).

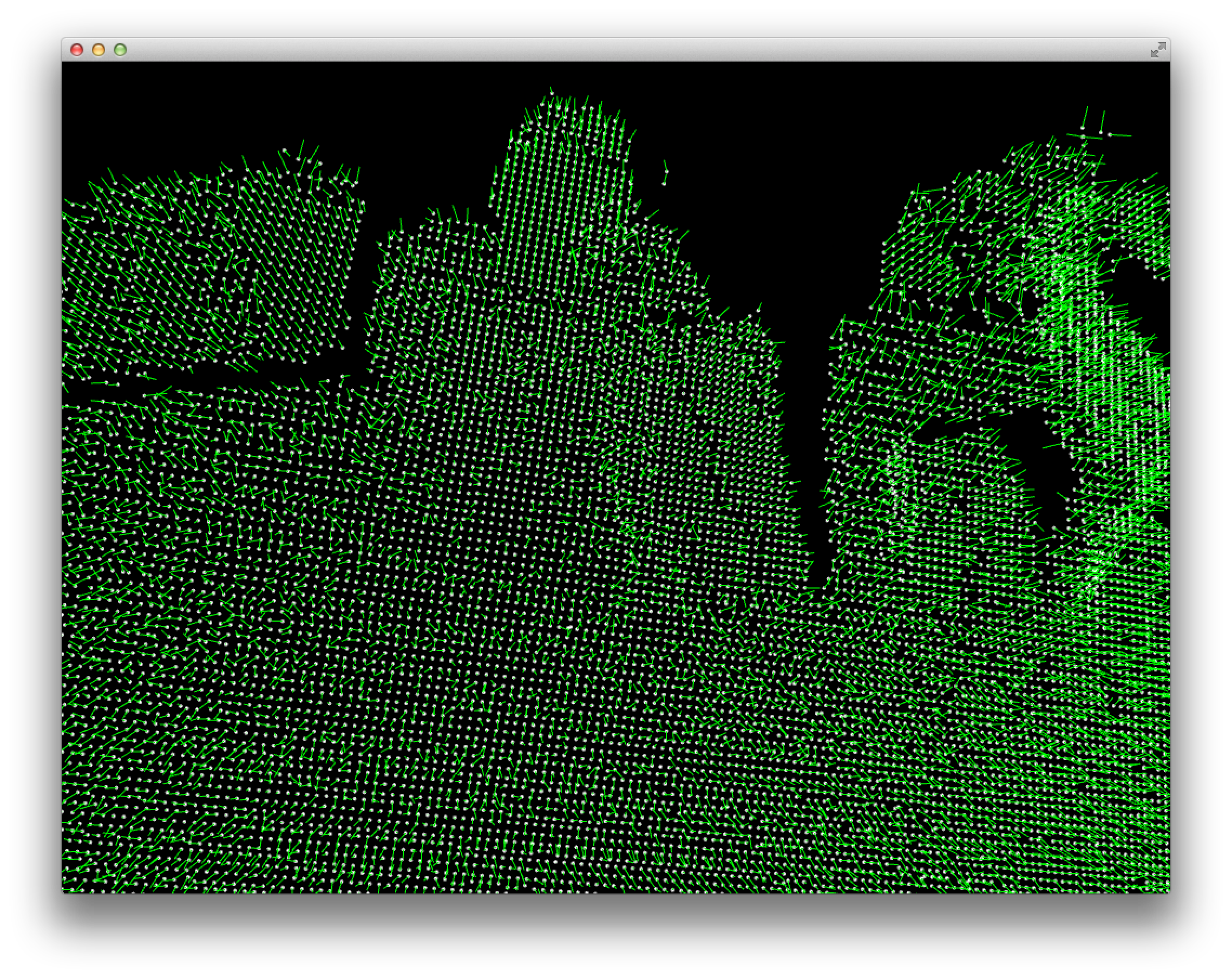
After much experimenting, I found that dramatically increasing the number of neighbors considered in the normal estimation. I'd initially considered 10 neighbors, but when I upped the number in to the hundreds was when I first starting seeing reults improve. At 200 neighbors, the number of non-zero adjacency entries crossed over 1 million (finally over 1% of the total entries.

num non-zero: 1366331/118200384 (0.0115594)
num components: 7251

And you can finally start to see some successful object segmentation (see especially the cylindrical and tall flat objects on the right:

At this point I decided that the segmentation results were insufficient to merit implementing the removal of internal points. As a next step I'd want to go back and implement the normal reprojection technique described in the paper for reducing noise in order to improve these segmentation results before proceeding.