Transforms: Wavelets, PCA, ICA
12.3) Consider a measurement of a three-component vector x, with x1 and x2 being drawn independently from a Gaussian distribution with 0 mean and unit variance, and x3 = x1 + x2.
a) Analytically calculate the covariance matrix of x

b) What are the eigenvalues?

C) Numerically verify these results by drawing a data set from the distribution and computing the covariance matrix and eigenvalues.
Code here: pca.py
import numpy as np
n = 100000
x1 = np.random.normal(0,1,n)
x2 = np.random.normal(0,1,n)
x3 = x1+x2
X = [x1,x2,x3]
c = np.cov(X)
print(c)
# Covariance matrix:
# [[ 1.00552305 -0.00540942 1.00011363]
# [-0.00540942 1.00327819 0.99786877]
# [ 1.00011363 0.99786877 1.9979824 ]]
e = np.linalg.eig(c)
print(e[0])
# Eigenvalues:
# [ 2.99277382e+00 1.00136031e+00 1.76529821e-15]
D) Numerically find the eigenvectors of the covariance matrix, and use them to construct a transformation to a new set of variables y that have a diagonal covariance matrix with no zero eigenvalues. Verify this on the data set.
Continuing the excerpt of pca.py above:
print(e[1])
# Eigenvectors (col major):
# [[-0.40445603 0.70928273 0.57735027]
# [-0.41202885 -0.70491056 0.57735027]
# [-0.81648487 0.00437217 -0.57735027]]
# Cov(y) = M * Cov(x) * M^T
cy = np.dot(np.dot(e[1].T,c), e[1].T)
print(cy)
#
# [[ 2.61908171 0.80509741 -0.50471862]
# [ 0.80509741 0.98241759 0.30643185]
# [-0.50471862 0.30643185 0.38716296]]
12.4) Generate pairs of uniform random variables {s1,s2} with each component contained in [0,1].
a) Plot these data.
Code here: ica.py.
import numpy as np
import matplotlib.pyplot as plt
n = 100
s1 = np.random.uniform(0,1,n)
s2 = np.random.uniform(0,1,n)
plt.scatter(s1,s2)
plt.show()
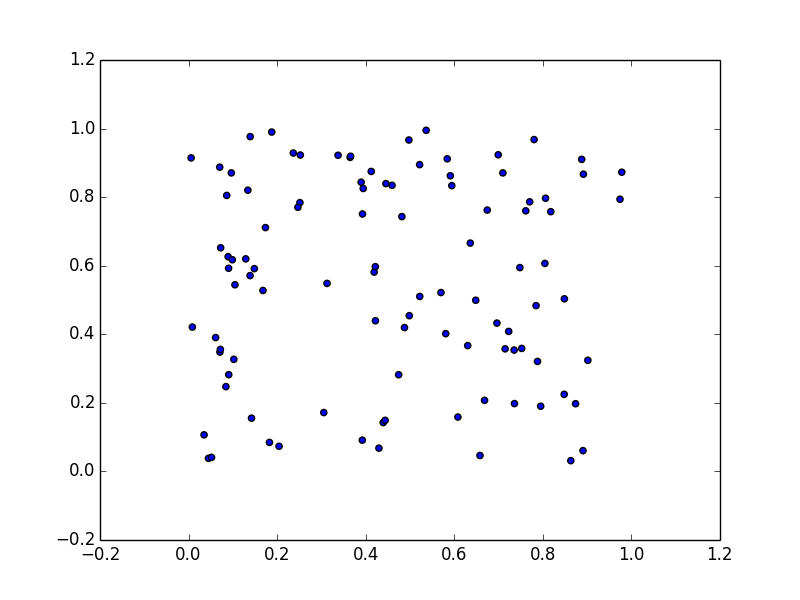
b) Mix them (x = A*s) with a square matrix A = [[1 2] [3 1]] and plot.
Continuing from ica.py...
S = np.column_stack([s1, s2])
A = [[1,2],[3,1]]
mix = np.dot(S,A)
plt.scatter(mix[:,0], mix[:,1])
plt.show()
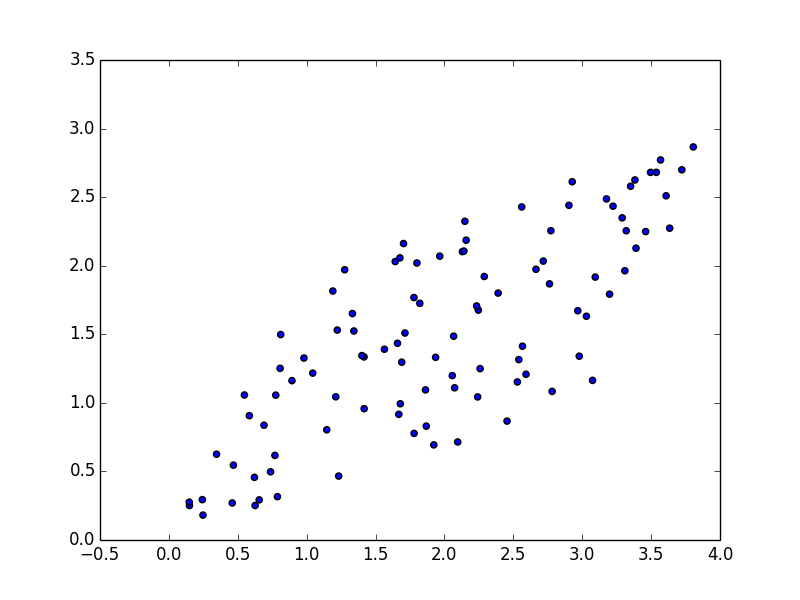
c) Make x zero mean, diagonalize with unit variance, and plot