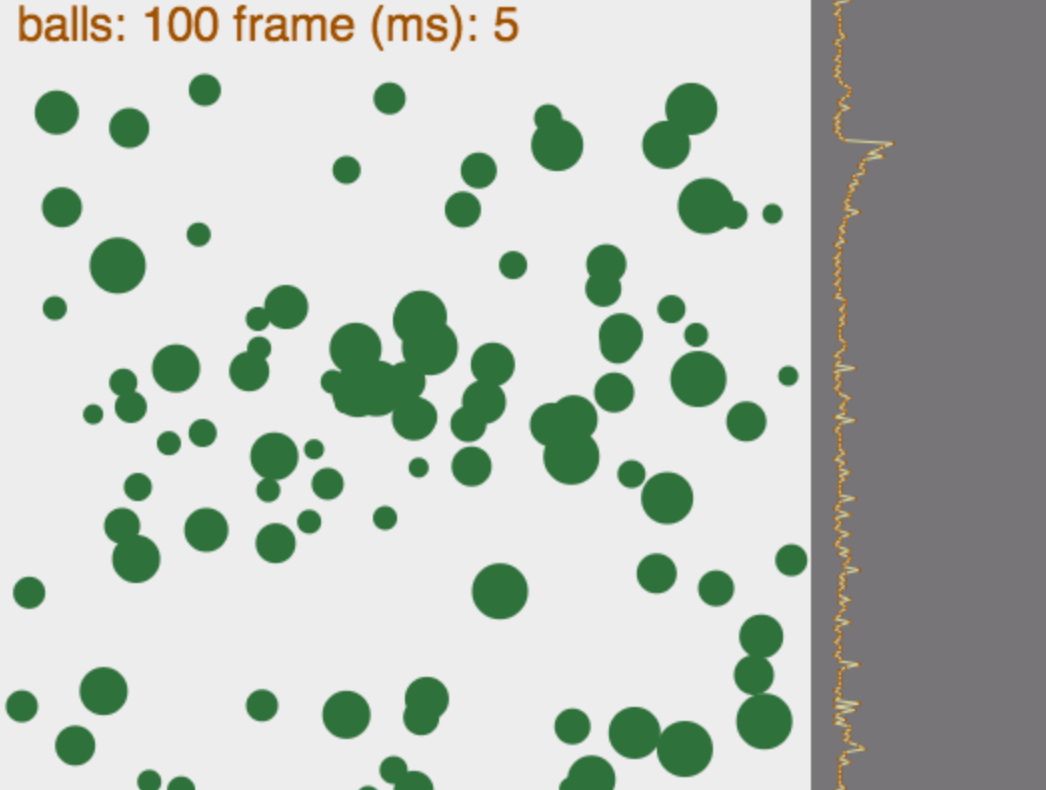
Our assignment this week was to bounce balls in many different ways. I took the opportunity to learn some web programming skills.
First, I implemented bouncing balls using the HTML5 canvas element with javascript. Click on the screenshot below to run it live. There is an array of states (x,y,dx,dy) that determine the ball trajectories. The plot on the left graphs the time taken to complete the cycle. In particular, you can see how the time is affected by other processes on your computer. Interestingly, google searching for queues in javascript (for tracking time histories) use push and shift on arrays, but if we keep lots of time points this calculation starts to make up a significant portion of the cycle time (shift is O(n)). Instead, for this application, we can keep track of the oldest entry in an array of time values. Each update we replace it, and we plot the data cyclically from this index.
After that, I decided to do a foray into WebGL. I've been wanting to learn more about shaders and the GL pipeline for a while, and the constraint of running in the browser is a great reason to push as much calculation as possible over to the GPU. Click the screenshot below to check out a bouncing head.
I started from a simple exmple of displaying a static triangle strip. I changed the code to include an element array buffer and use gl.TRIANGLES instead of gl.TRIANGLE_STRIP. That way I could specify the vertices and facets of the geometry separately, and not have to worry about the ordering of the vertices. I started by testing on a simple tetrahedron. I added the wireframe bounding box in the same way, specifying corners and connecting them with gl.LINES.
I grabbed the basic callbacks for rotation and zoom from another example. I had to tweak them a bit to work with my method of frame drawing, but eventually, I could display and color a mesh bouncing inside a wireframe box, with rotation and zoom (click+drag and scroll). I didn't get around to adding vertex normals and lighting, but I don't think that will be very hard.
In order to generate the variables containing vertex and triangle information, I wrote a python script using Numpy to generate simple javascript declarations from a binary STL file. I started with a code snippet from the web, and replaced their python set conversion with a call to Numpy's unique. Normally unique will flatten the input array and consider only one dimensional arrays. To get around this, we generate a view of the vertex array that preserves the last dimension. Then unique operates on points in three space. The script is below:
#!/usr/bin/env python
# writing js data structure for a mesh
import sys
from numpy import *
from struct import unpack
def read_binary_stl(fname):
#all numpy binary stl reader
#adapted from http://sukhbinder.wordpress.com/2013/11/28/binary-stl-file-reader-in-python-powered-by-numpy/
#but use numpy.unique instead of python set conversion
fp = open(fname, 'rb')
Header = fp.read(80)
nn = fp.read(4)
Numtri = unpack('i', nn)[0]
record_dtype = dtype([
('normals', float32,(3,)),
('Vertex1', float32,(3,)),
('Vertex2', float32,(3,)),
('Vertex3', float32,(3,)),
('atttr', '<i2',(1,) )
])
data = fromfile(fp , dtype = record_dtype , count =Numtri)
fp.close()
v1= data['Vertex1']
v2= data['Vertex2']
v3= data['Vertex3']
#n= data['normals']
X = vstack((v1,v2,v3))
#use a new view to do 3 dimensional unique calculation
Xc = ascontiguousarray(X).view(dtype((void, X.dtype.itemsize * X.shape[1])))
_,idx,inv = unique(Xc, return_index=True,return_inverse=True)
X = X[idx] #grab unique points
n = shape(v1)[0]
tris = dstack((arange(n),arange(n)+n,arange(n)+2*n))[0]
tris = inv[tris] #map triangle indices to unique point indices
return tris,X
def write(jsname,(tris,X)):
f = open(jsname,'w')
xmax = amax(X,axis=0)
xmin = amin(X,axis=0)
X = (X - (xmin+xmax)/2)/amax(xmax-xmin)
f.write('var mesh_vertices = [')
for x in X:
f.write('%.4f,%.4f,%.4f,'%tuple(x))
f.write('];\n')
f.write('var mesh_colors = [')
x0_max = amax(X[:,0])
for x in X:
f.write('%.4f,%.4f,%.4f,%.4f,'%(x[0],x[1],x[2],.7))
f.write('];\n')
f.write('var mesh_elements = [')
for tri in tris:
f.write('%d,%d,%d,'%tuple(tri))
f.write('];\n')
def main():
if len(sys.argv) != 3:
print 'usage: mesh_writer meshname jsname'
sys.exit(0)
meshname = sys.argv[1]
jsname = sys.argv[2]
write(jsname,read_binary_stl(meshname))
if __name__ == '__main__':
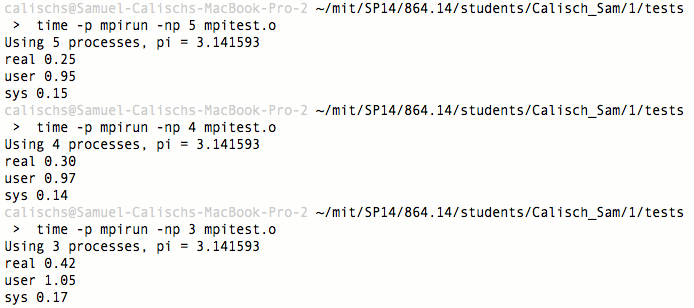
main()After the web stuff, I also tooled around with Neil's pi calculation examples in MPI. This page was helpful in figuring out how the script works.
Finally, I started playing with Petsc, in the name of making realistically deforming bouncing balls, among other things. Not surprisingly, there are python bindings at Petsc4py. I installed petsc with Homebrew and used pip install petsc4py==dev. Then I set the environment variable to point at the homebrew installation with export PETSC_DIR=/usr/local/Cellar/petsc/3.4.3/. To test, I opened a python session and successfully imported petsc4py.
I went to run a demo and I get an error about petsc being installed without x windows. Reading online, this is a mavericks thing... still working it out.