Constrained optimization: Problems 16.1, 16.2, 16.3, 16.4, 16.5

For work this week, I had to fix some problems with last week's routines. After some debugging, I determined that my line search had some problems, in particular when doing its initial bracketing near a critical point of the objective. I wrote a new line search based on Numerical Recipes' golden routine. Then I finished writing conjugate gradient based on this new line search.

I got excited by the compressed sensing problem, so I mostly ignored the other problems...

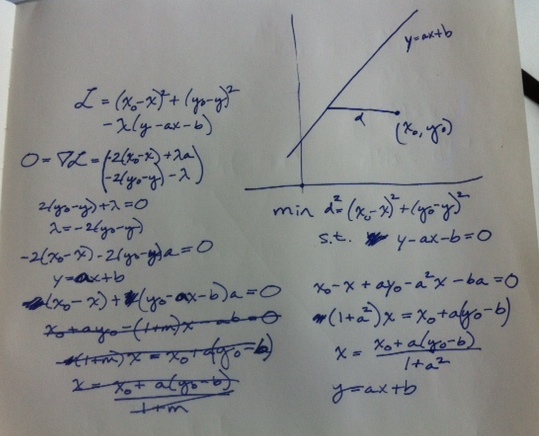
Use Lagrange multipliers to find the closest point on a line to another given point.

Re-implement Cleve Moler's compressed sensing example, using a discrete fourier transform instead of the discrete cosine transform, and using your own constrained L1 minimization routine.

In that cool article, Cleve shows how assuming sparsity allows you to reconstruct a signal while sampling a waveform at a rate considerably lower than the Nyquist frequency. He uses the L1 magic toolbox for matlab from Justin Romberg and Emmanuel Candes to find the most sparse signal that is consistent with his samples, and lo and behold, the result looks great.

For this problem, I worked from an IPython notebook, you can access the generated html here.

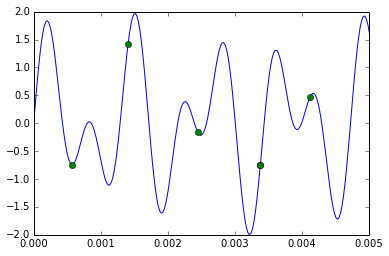
This shows the samples, along with the reconstructed signal.

In the process of working on this problem and doing background reading, I came to see why Cleve likely used the discrete cosine transform, as opposed to the discrete fourier transform. If we want to do a more robust job minimizing the L1 norm under the linear constraint, we can recast the problem as a mathematical program. In particular, if the matrices and vectors involved are real valued, we can cast the problem as a linear program (See this background material for the L1 magic toolbox). This brings all kinds of nice results on global optimality and feasibility, as well as a lot of nice freely available libraries. If the matrices and vectors are complex valued (as ours are), the problem can be recast as a second-order cone problem and solved nearly as efficiently as a linear program.

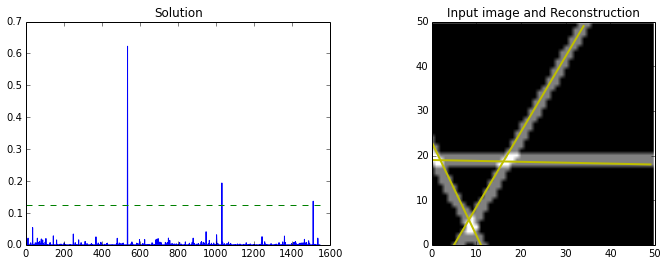
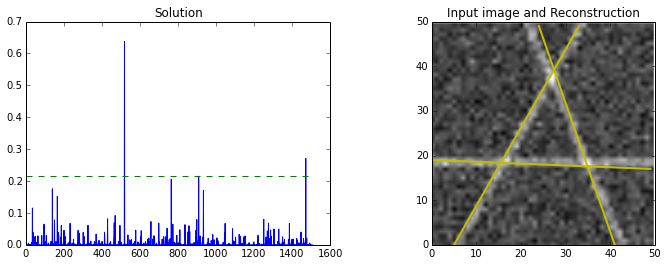
To explore using mathematical programming for this compressed sensing framework, I implemented a feature detector based on the Hough transform. I have a bunch of project ideas that require reliable feature recognition in drawings, and I thought this might be more robust than using the Hough transform alone. Below is a picture of the Hough circle transform on a bitmap of a part. As you can see, enforcing sparsity would be nice!

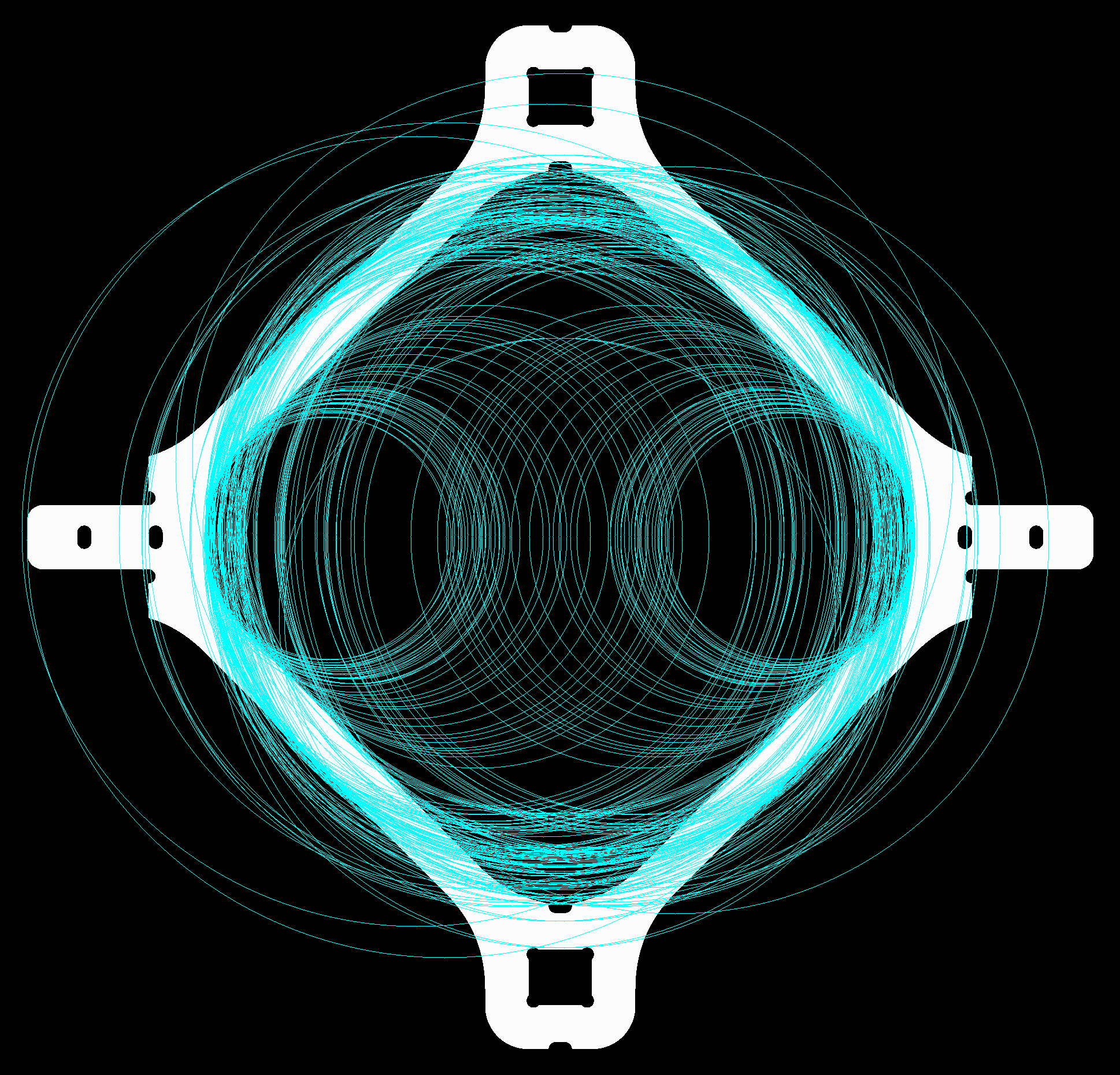
For this project, I also worked in an IPython notebook, you can access the generated html here. Nearly all of the math comes from this paper and the documentation for the L1-Magic toolbox.

Below are two trials of this implementation. In the first, I generated a bitmap with three intersecting straight lines. The compressed sensing framework fineds