Problems 8.1, 8.2, 8.3, 8.4
Stability of finite differences for the wave equation.

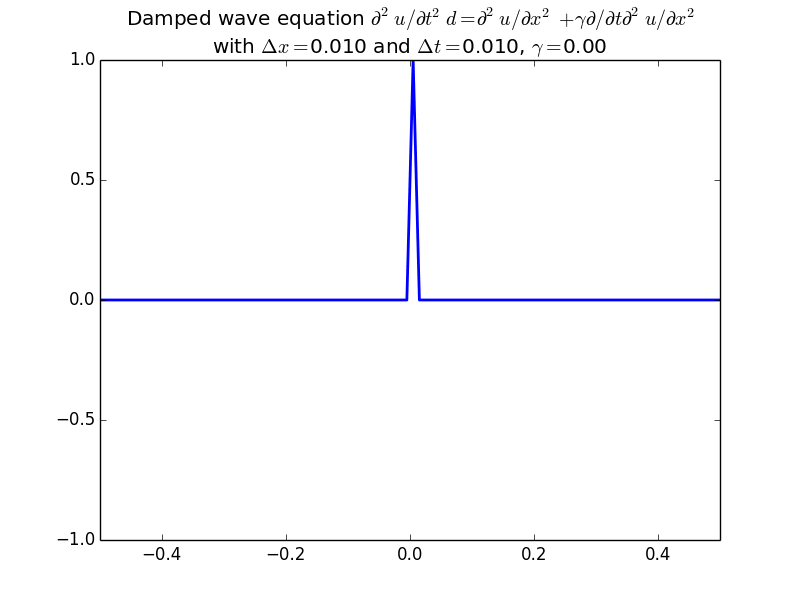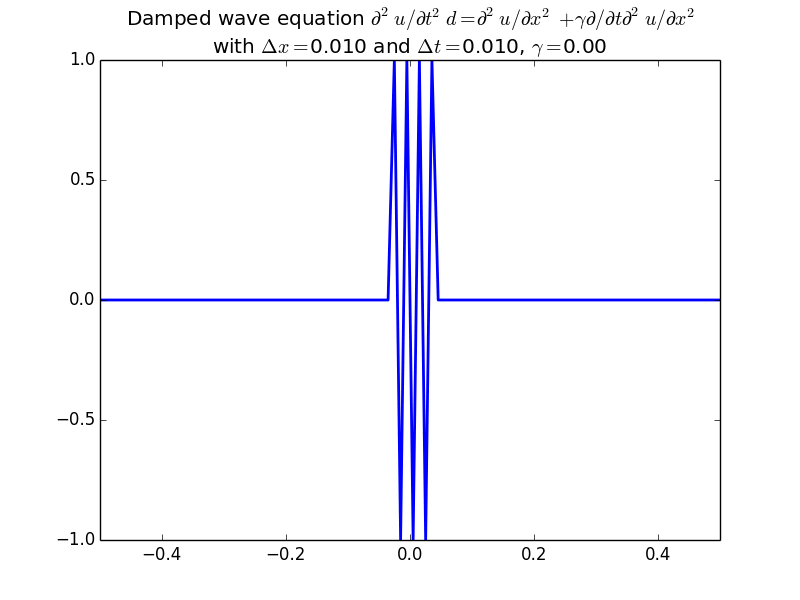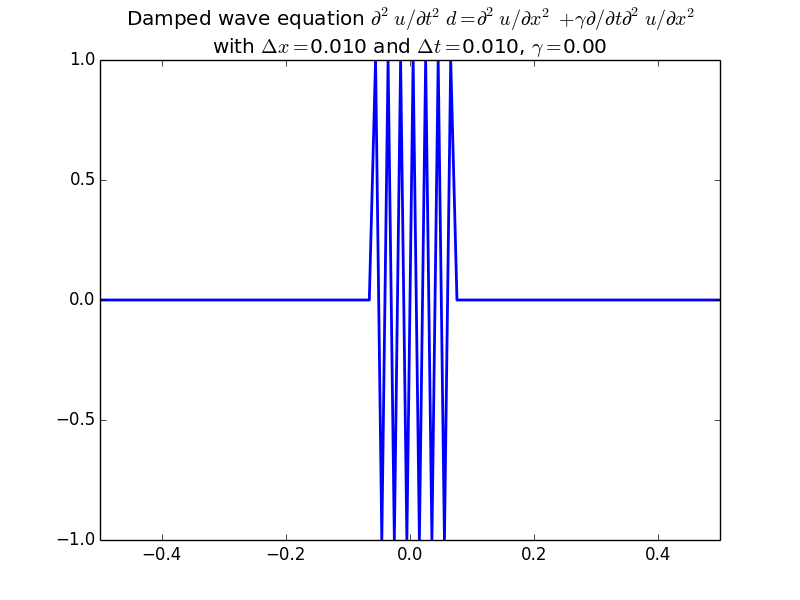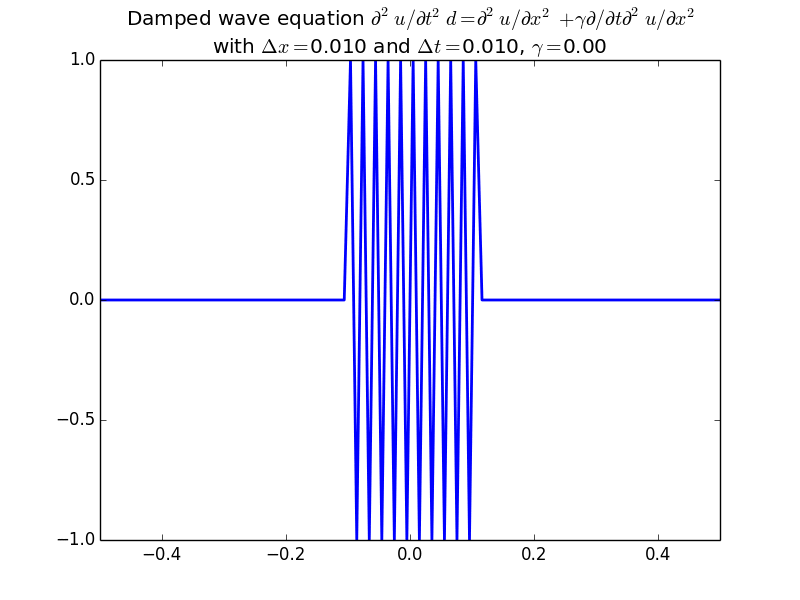
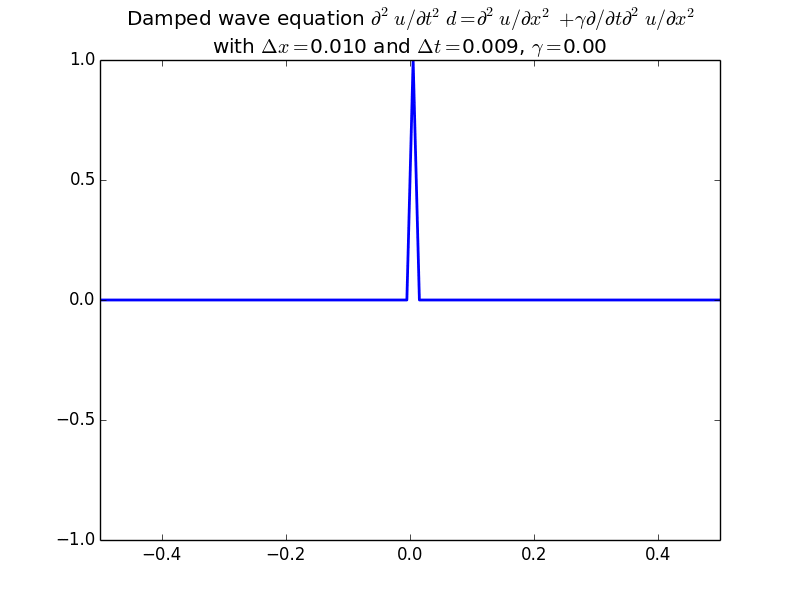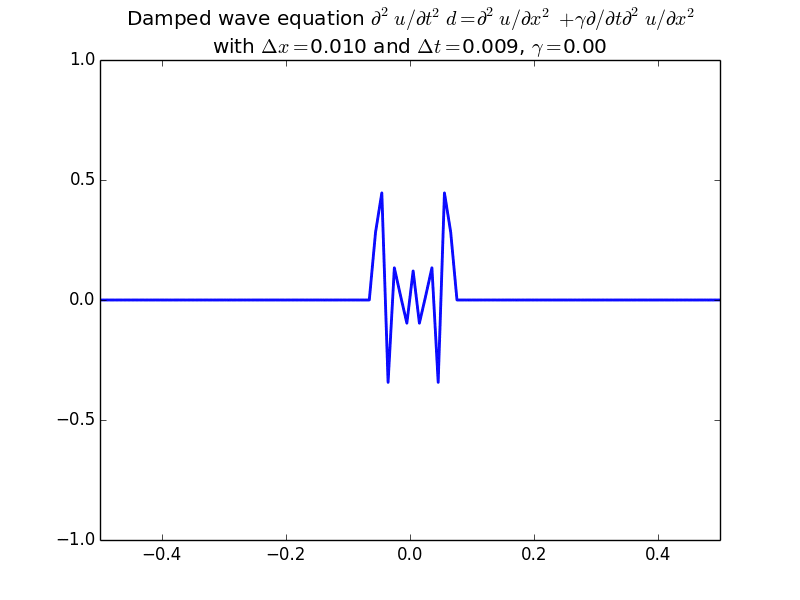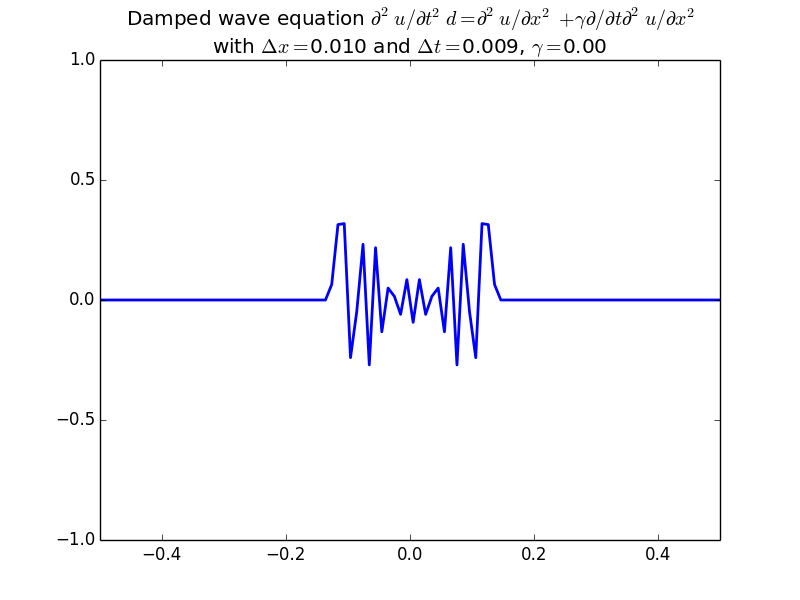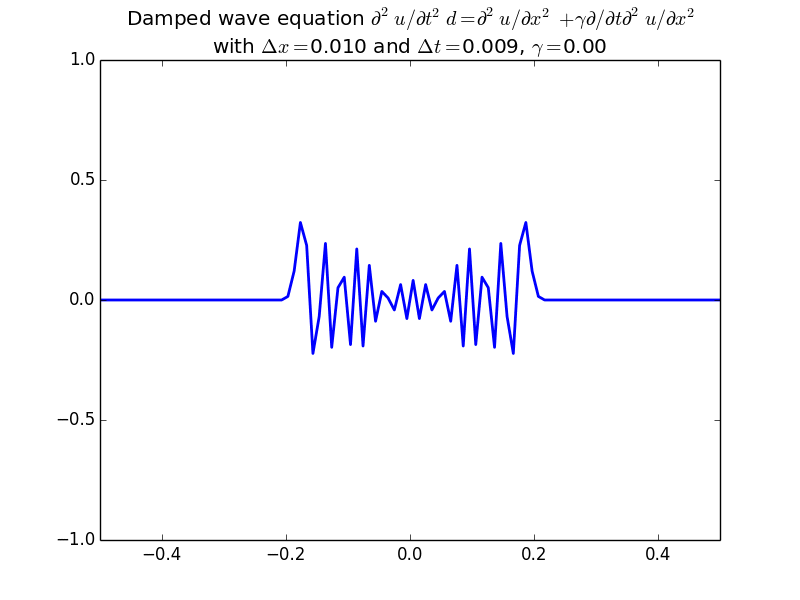
With damping:

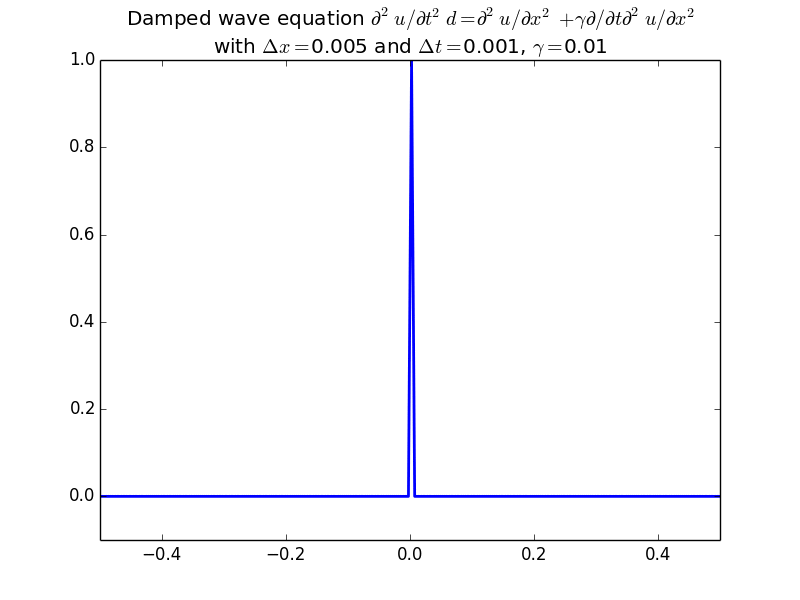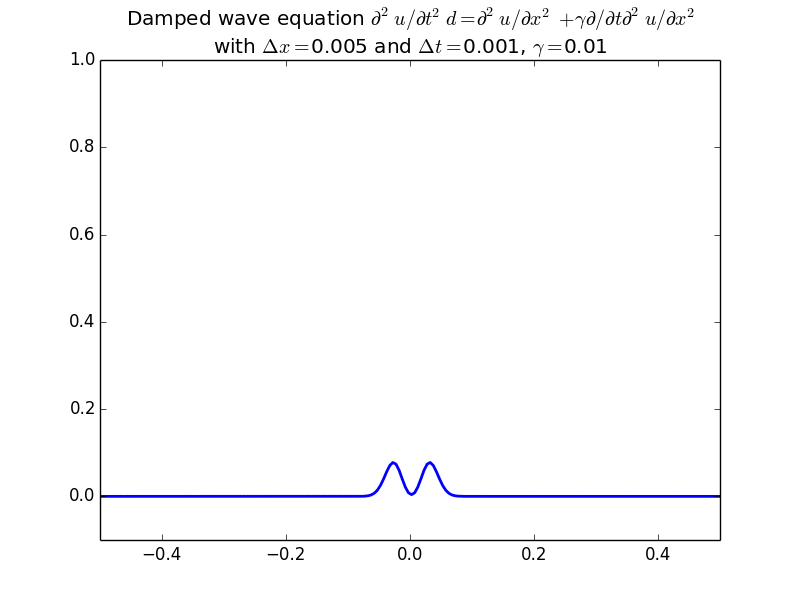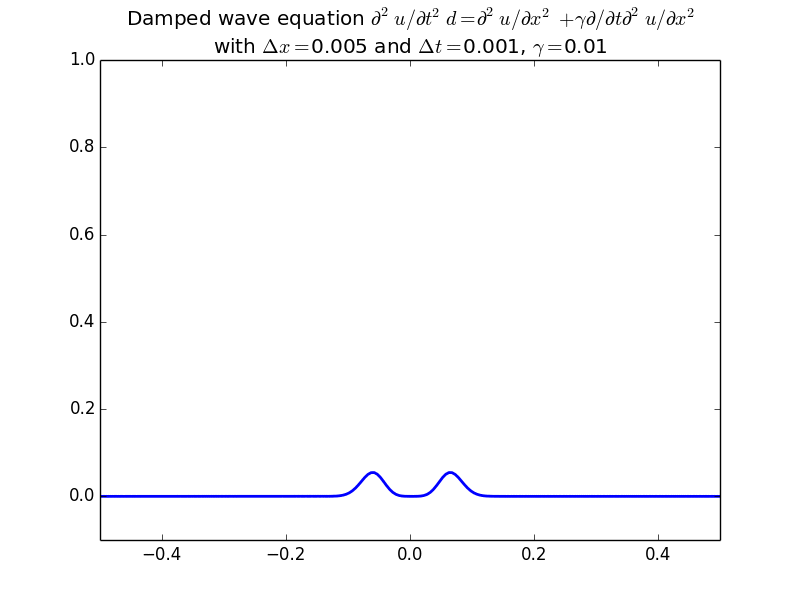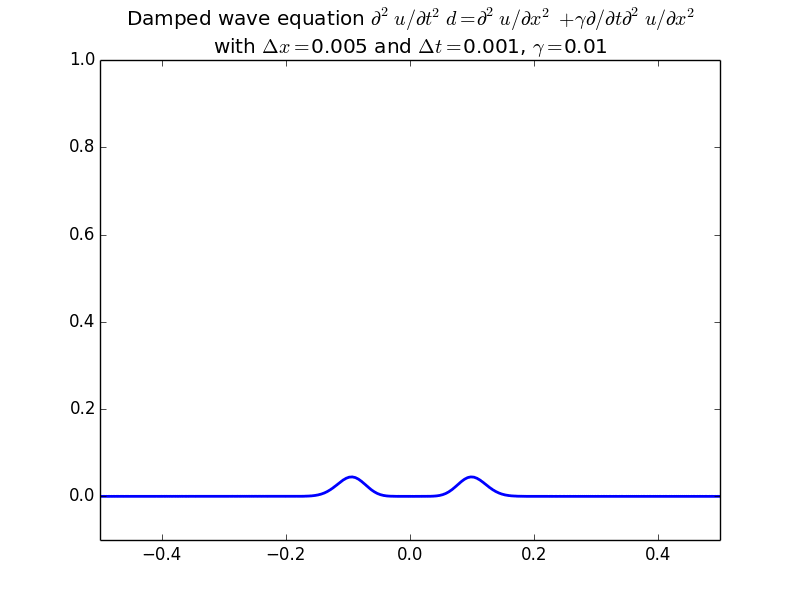
With more realistic initial conditions:
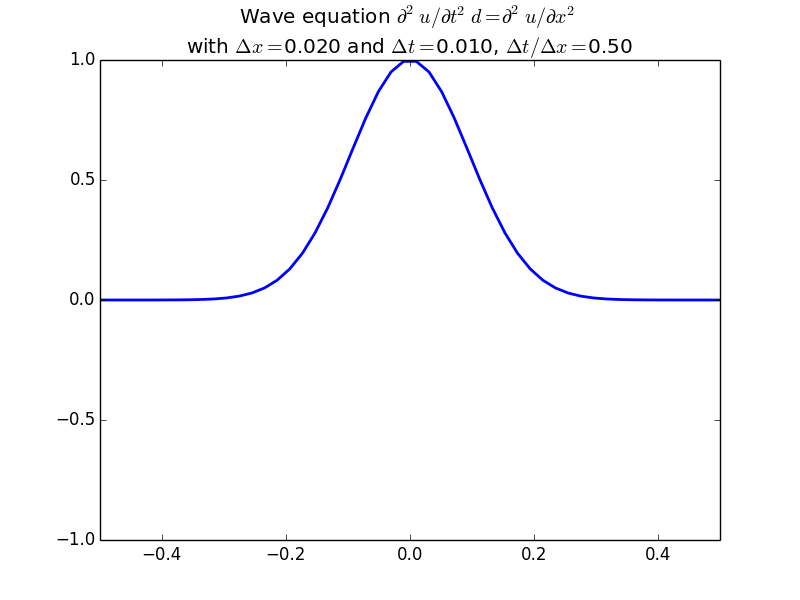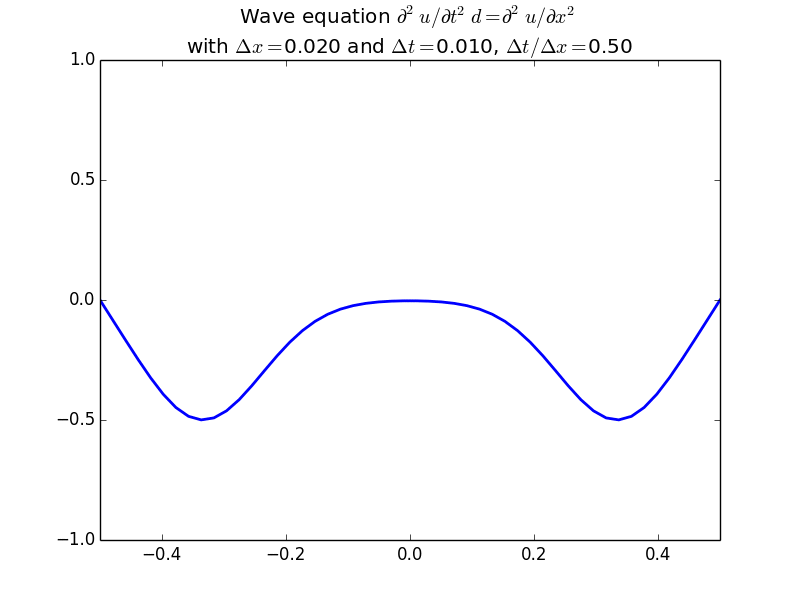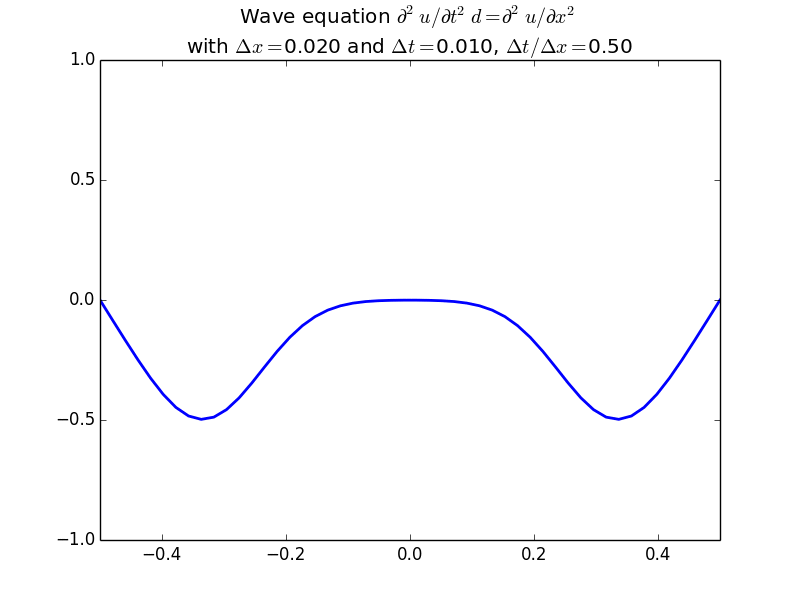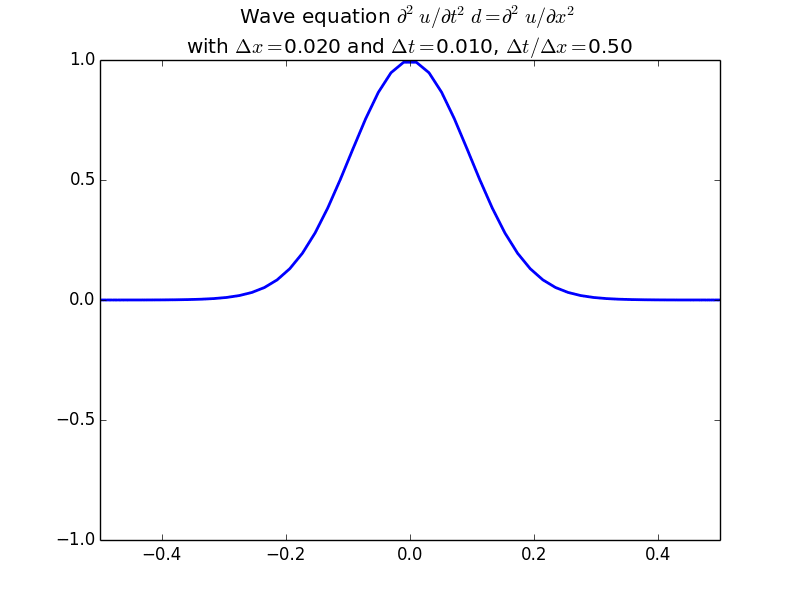
This scheme generalizes very easily to two-dimensions:
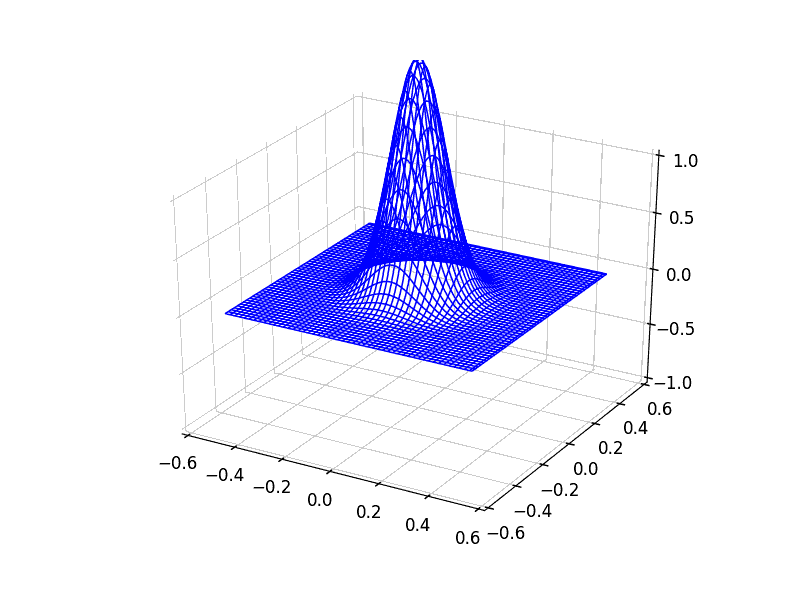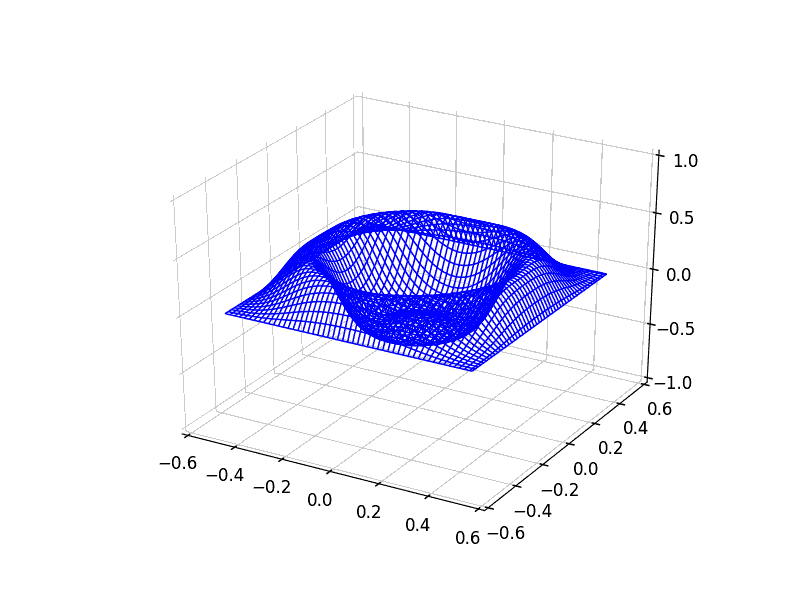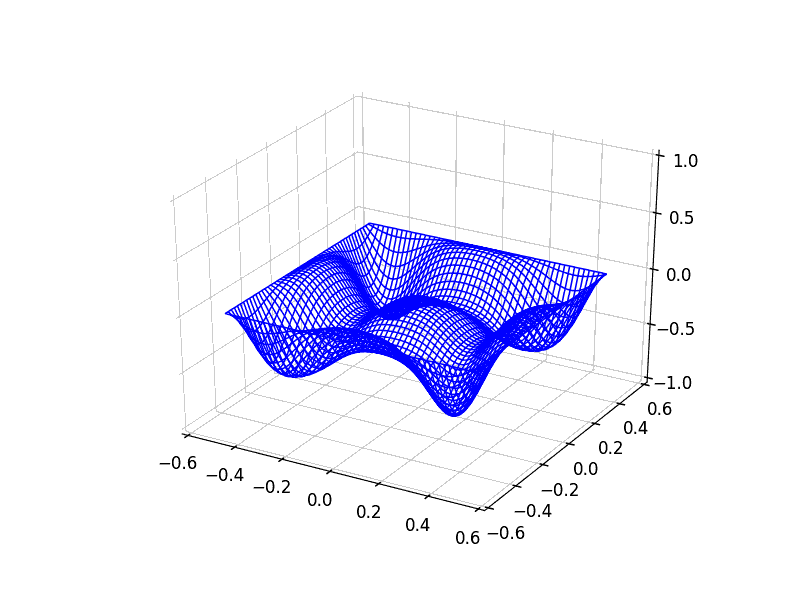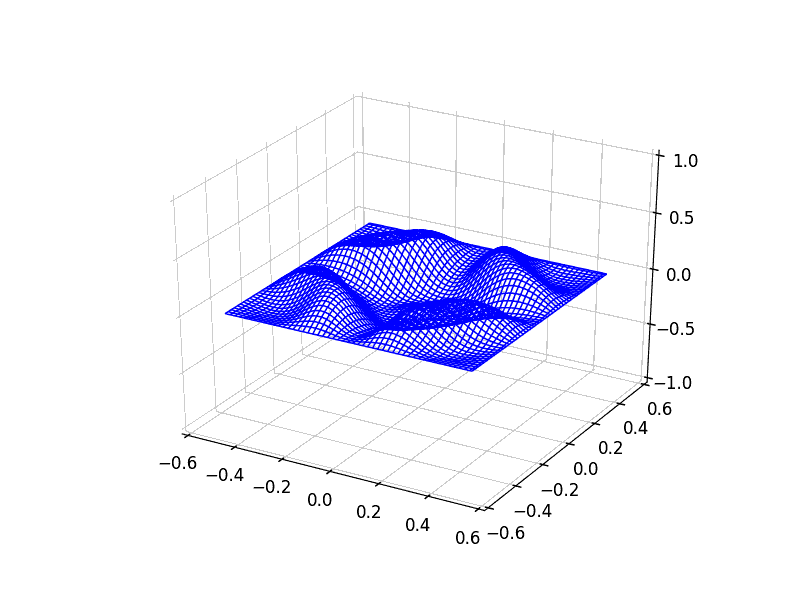
1D diffusion on 500 sites.
Python for 8.2 and Cython for tridiagonal solve
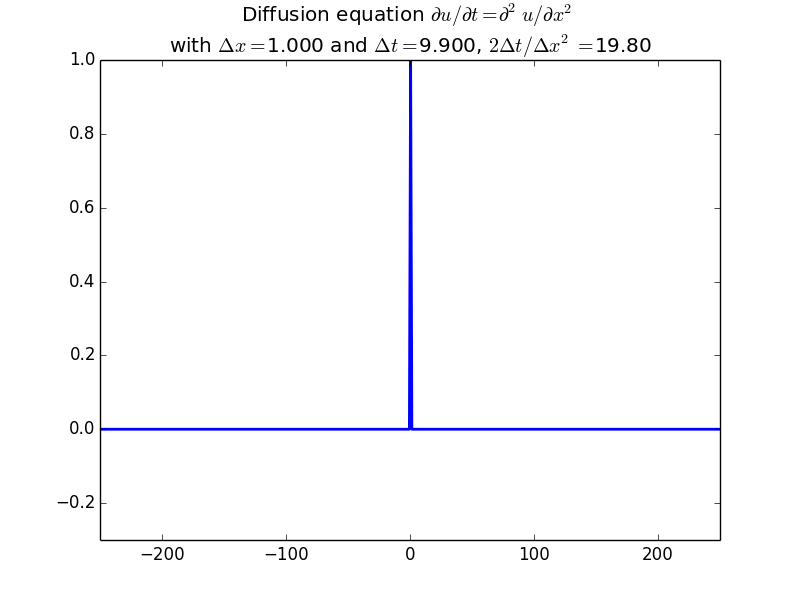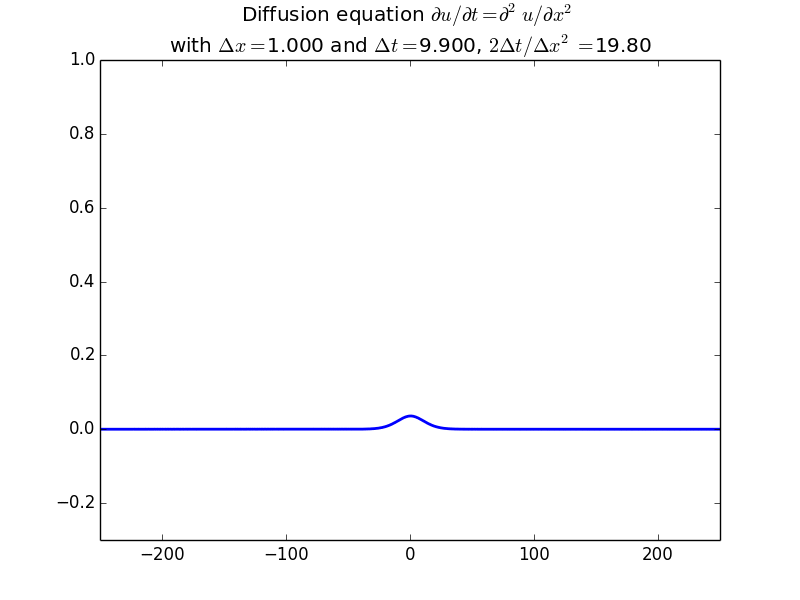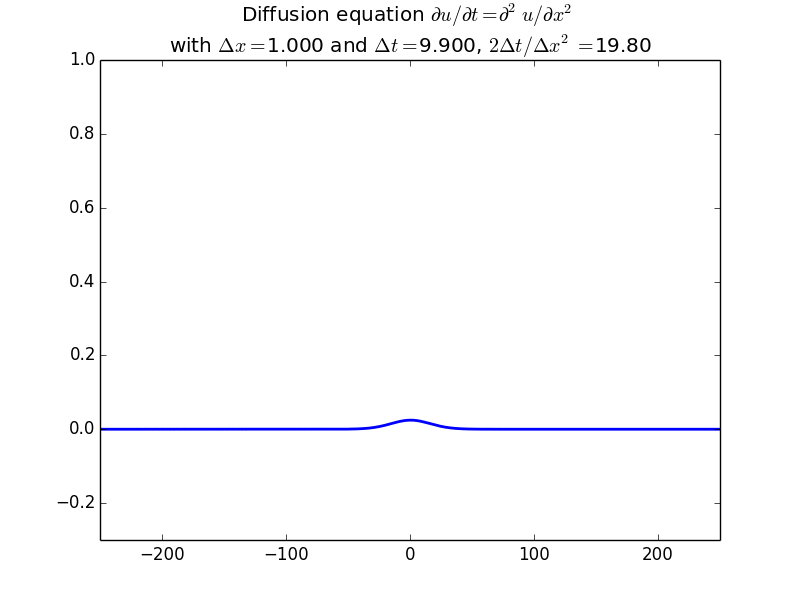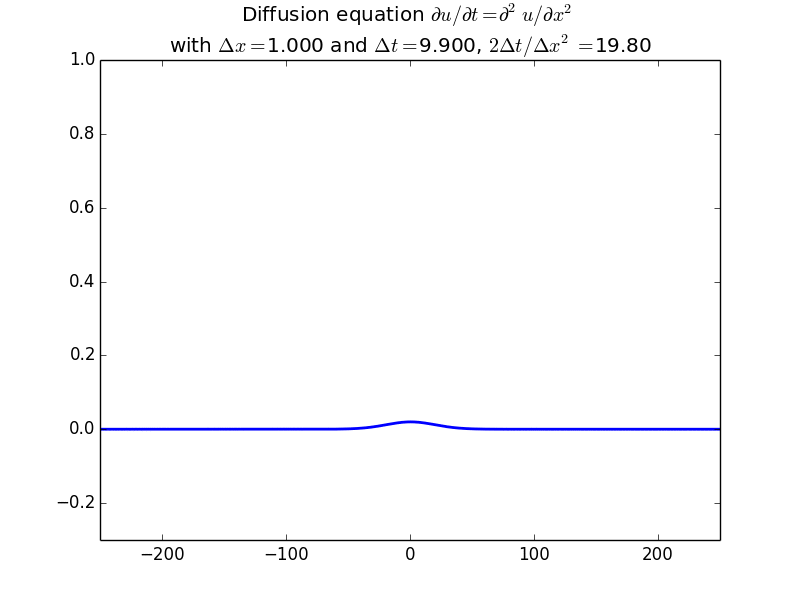
Explicit solutions:
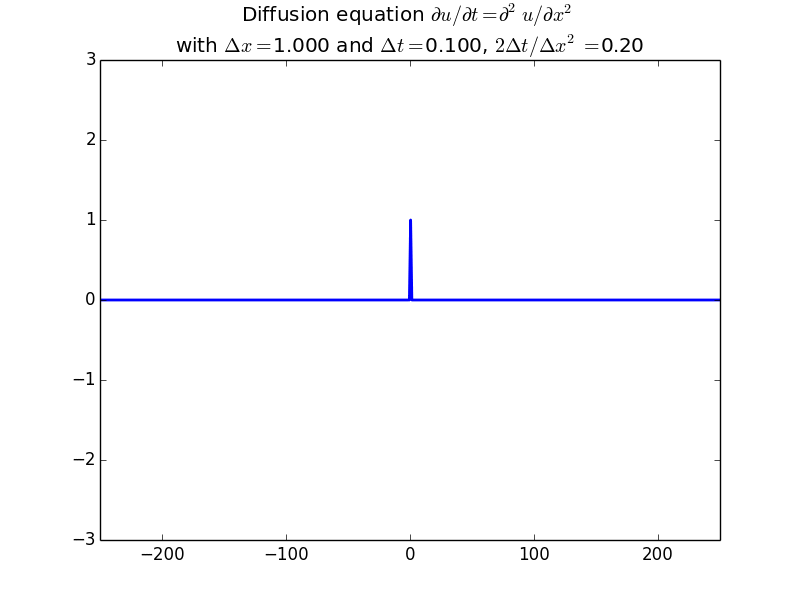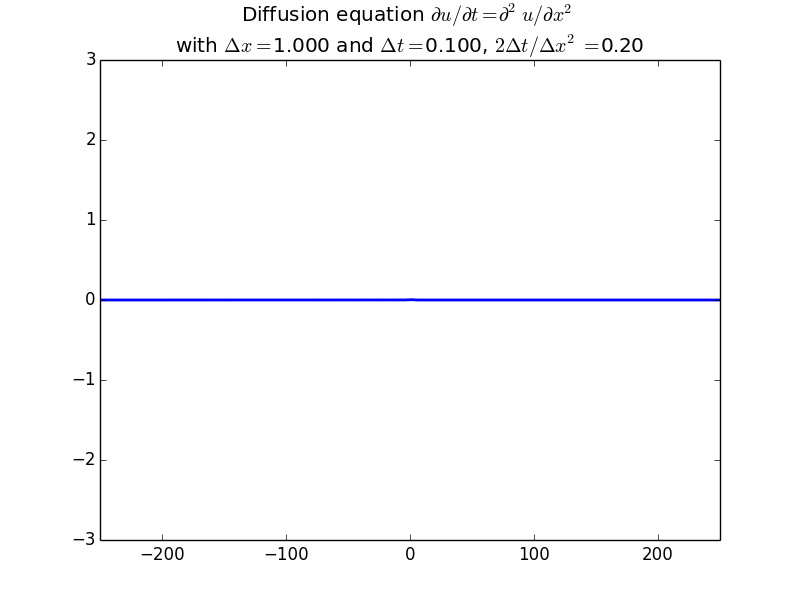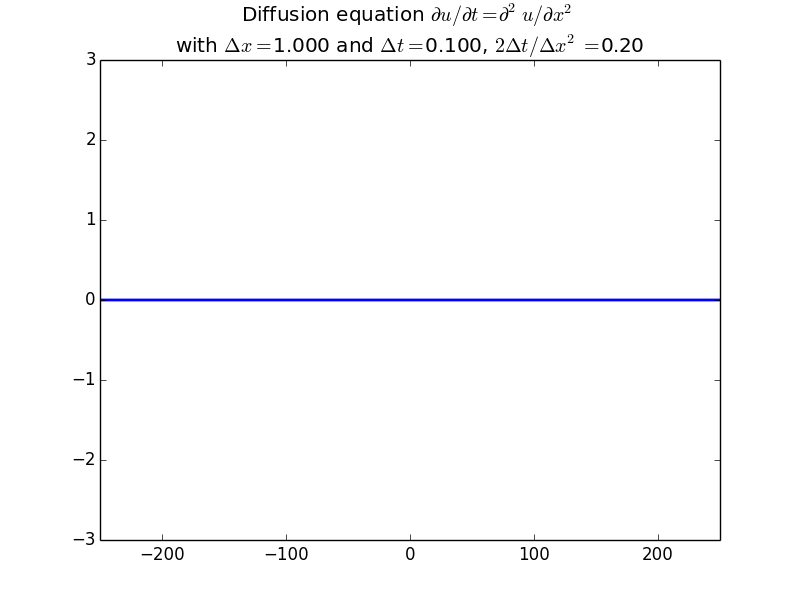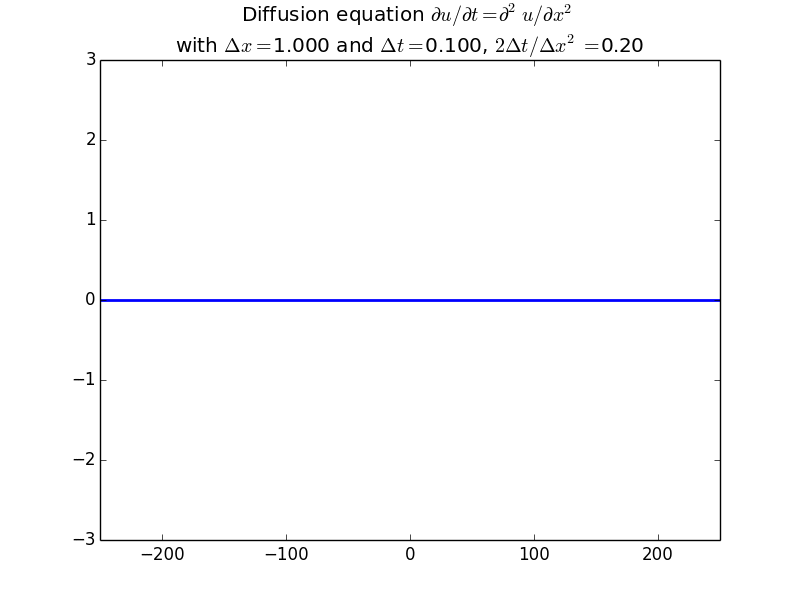
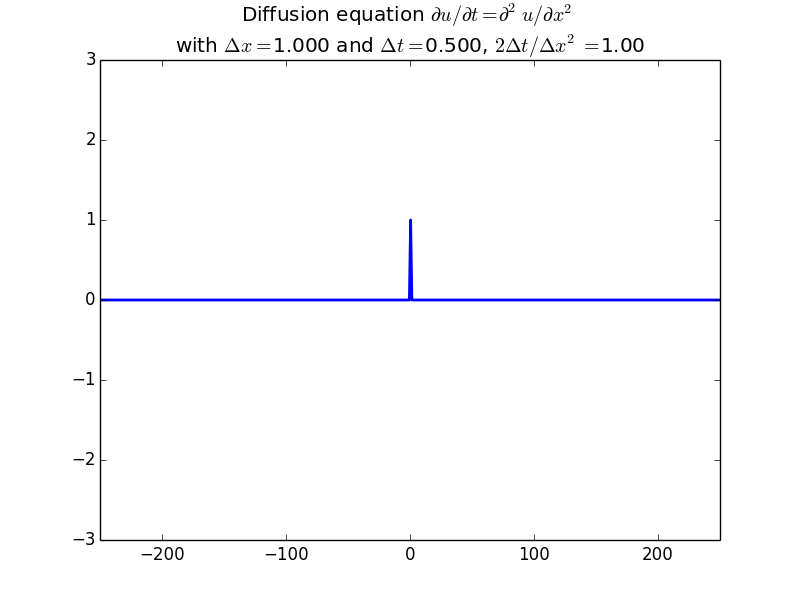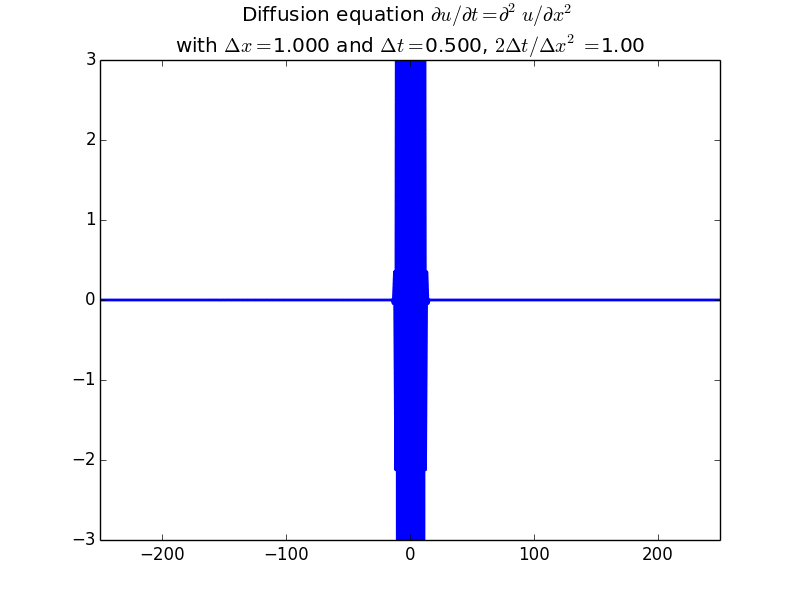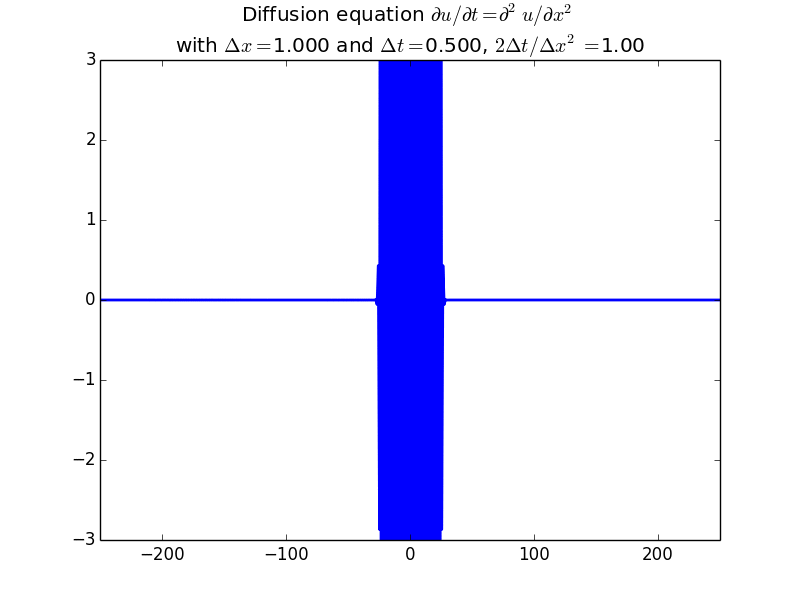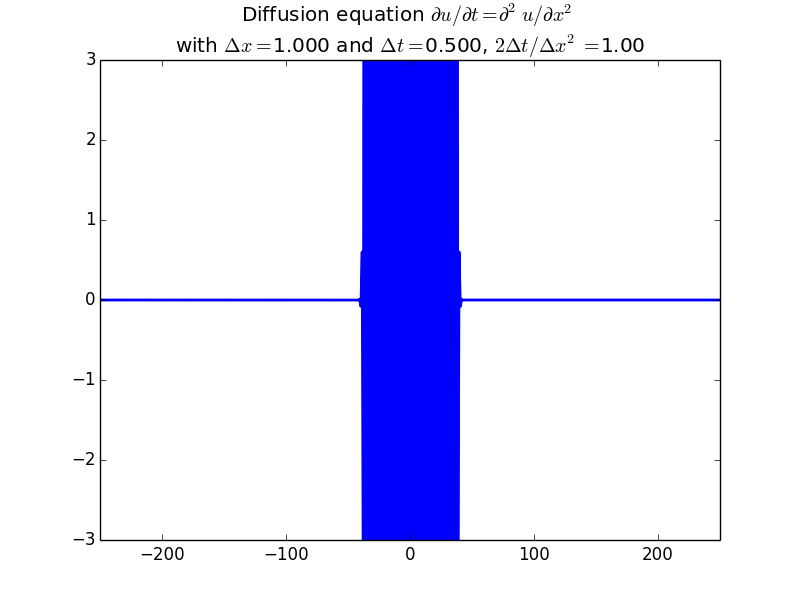
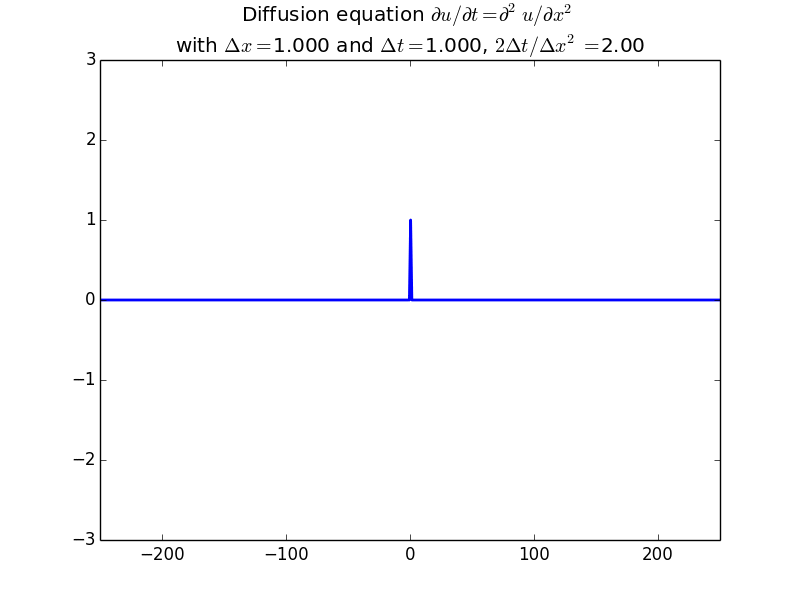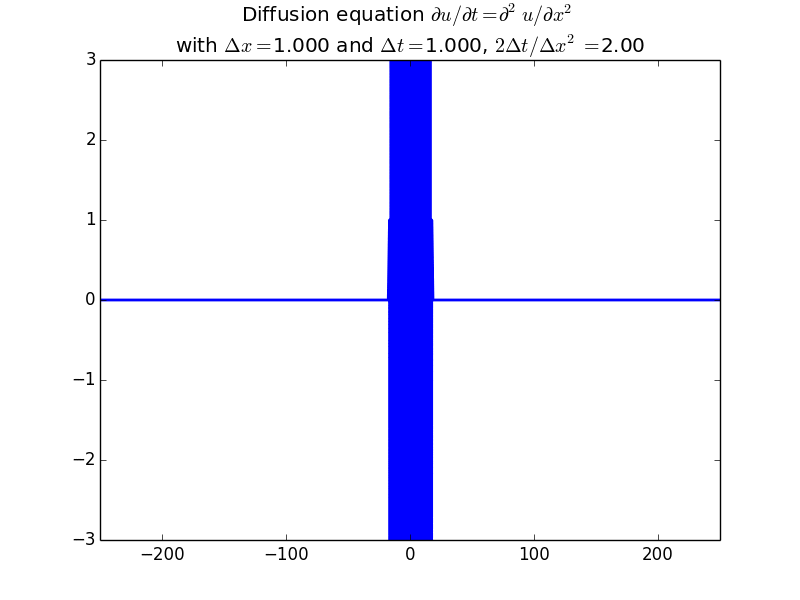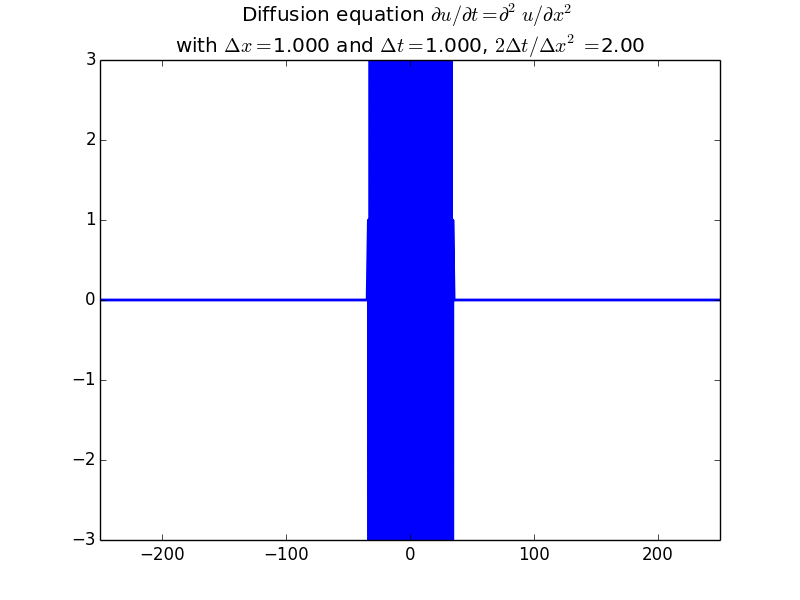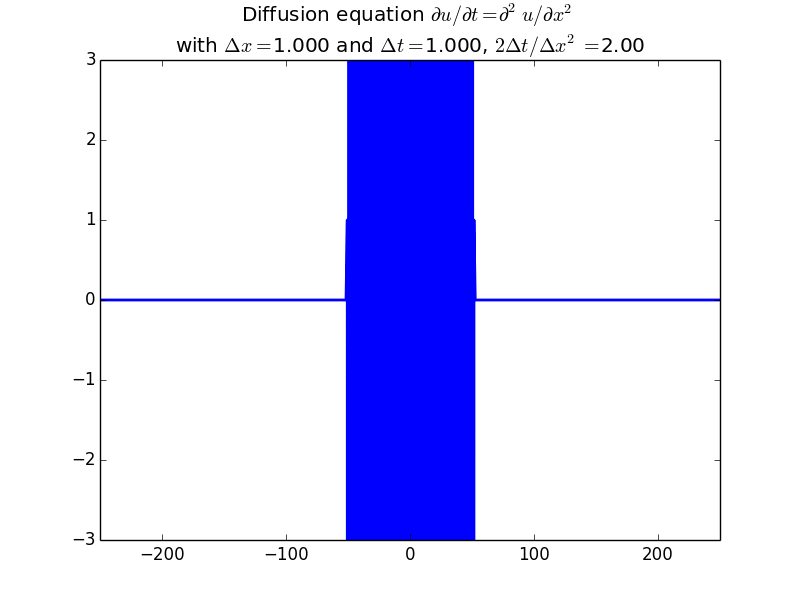
Implicit solutions:
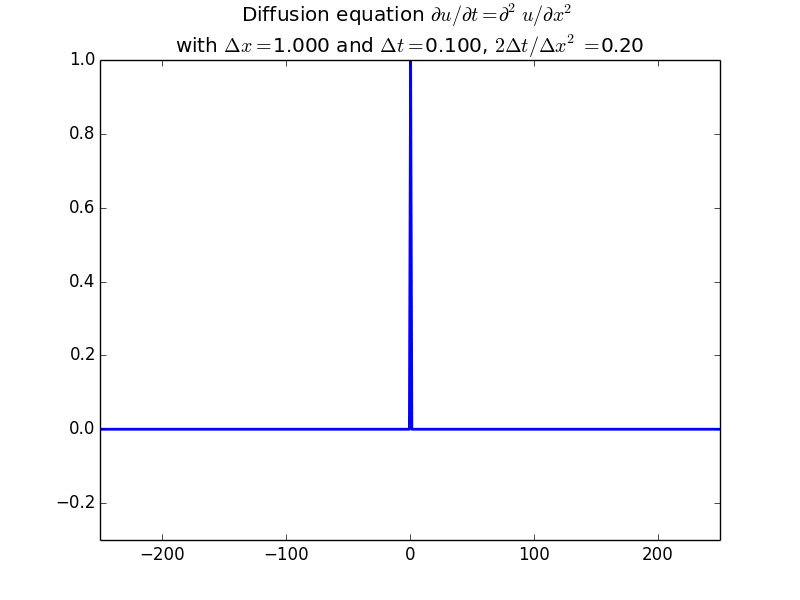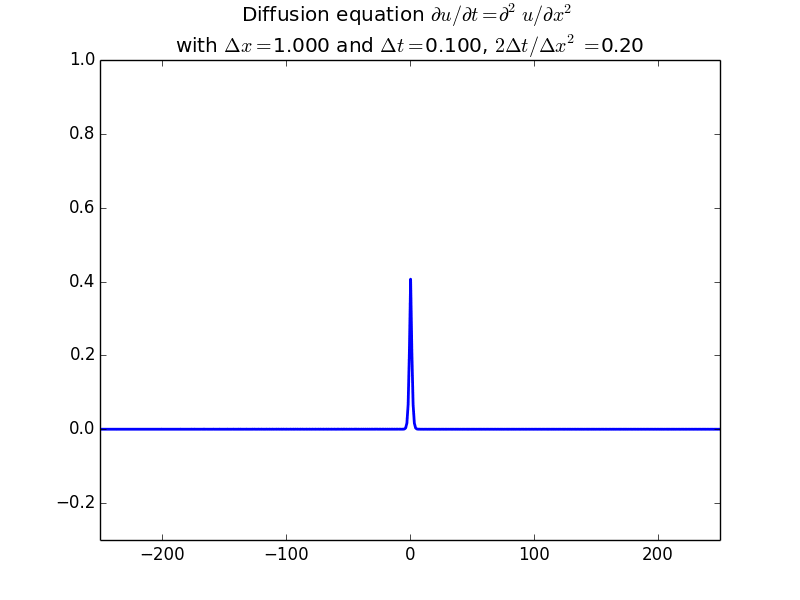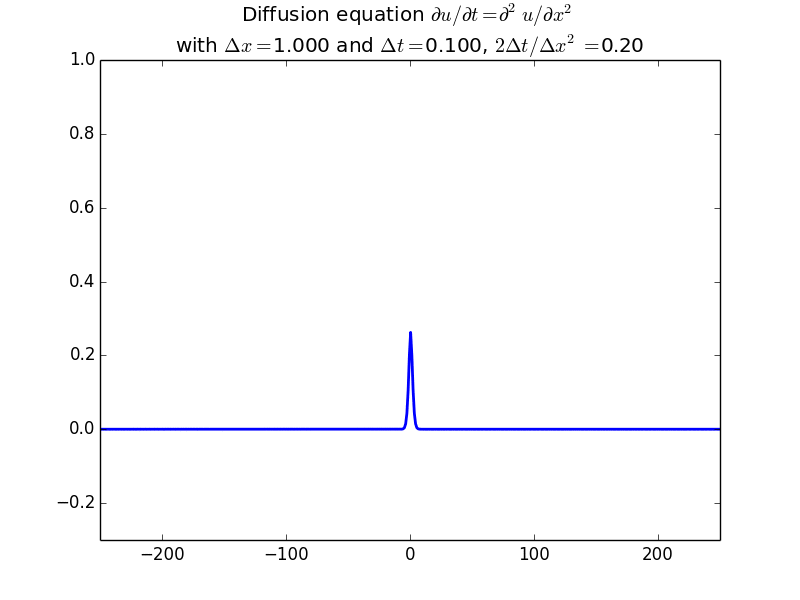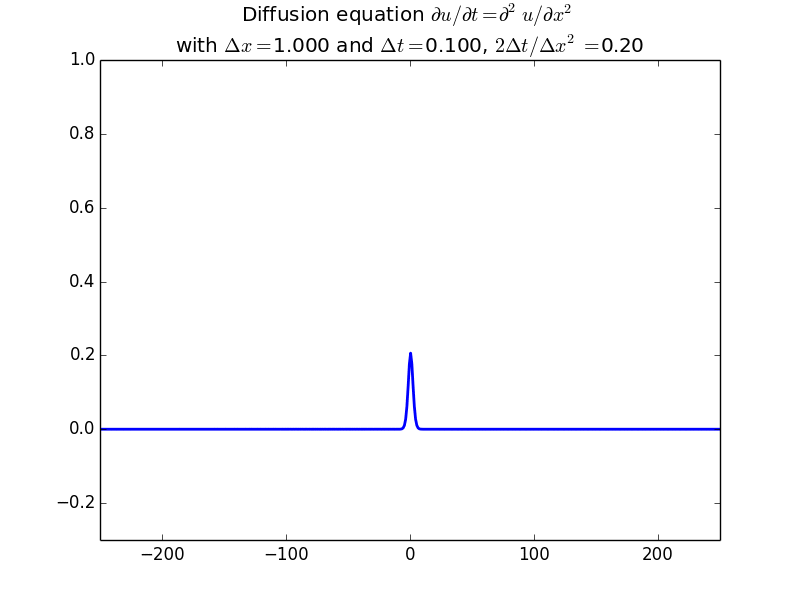
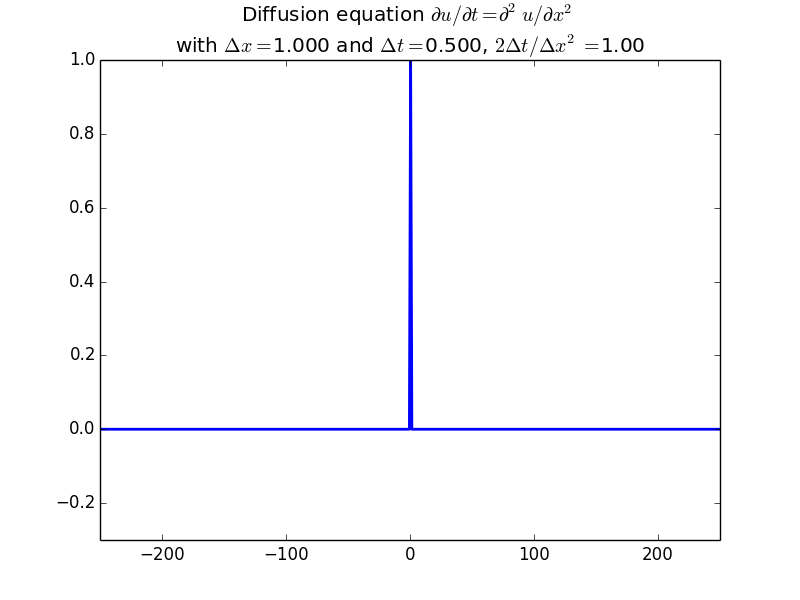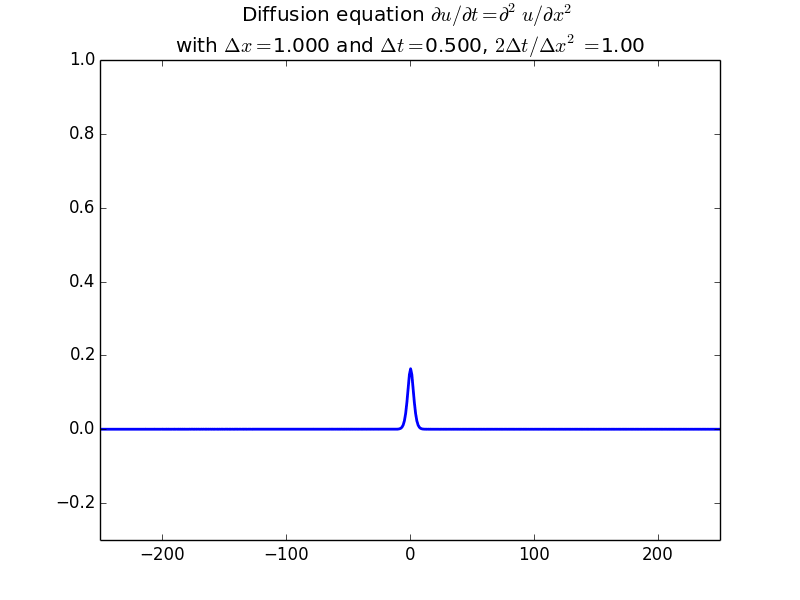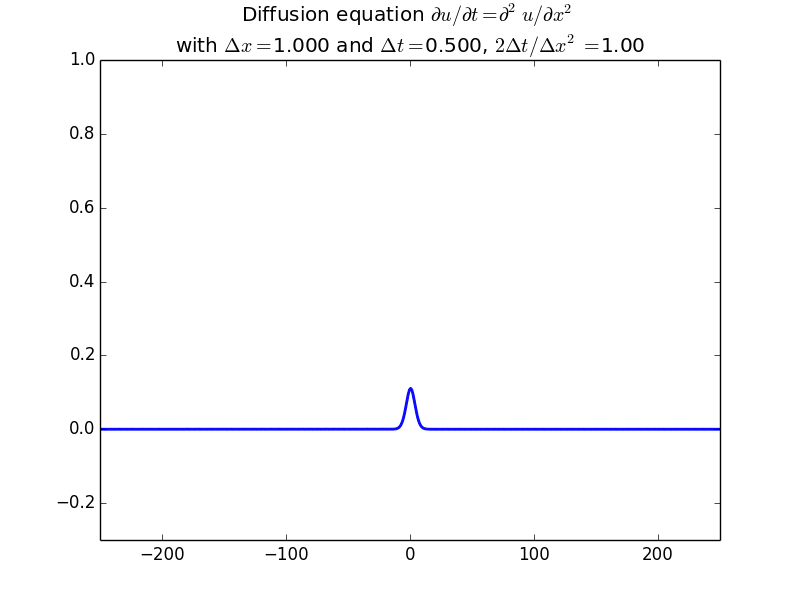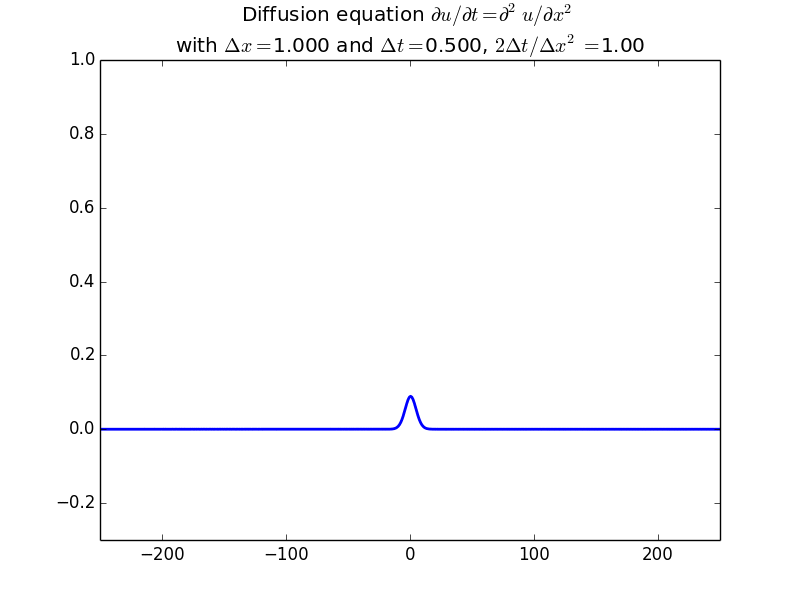
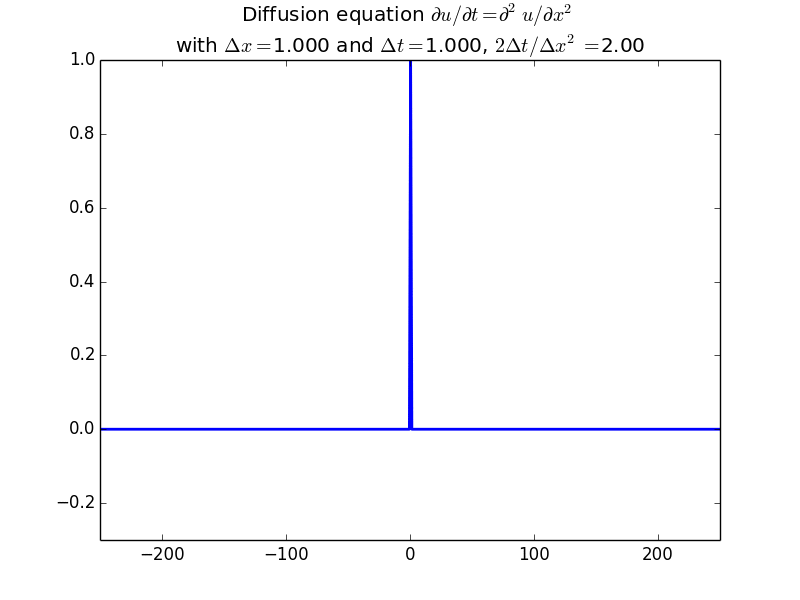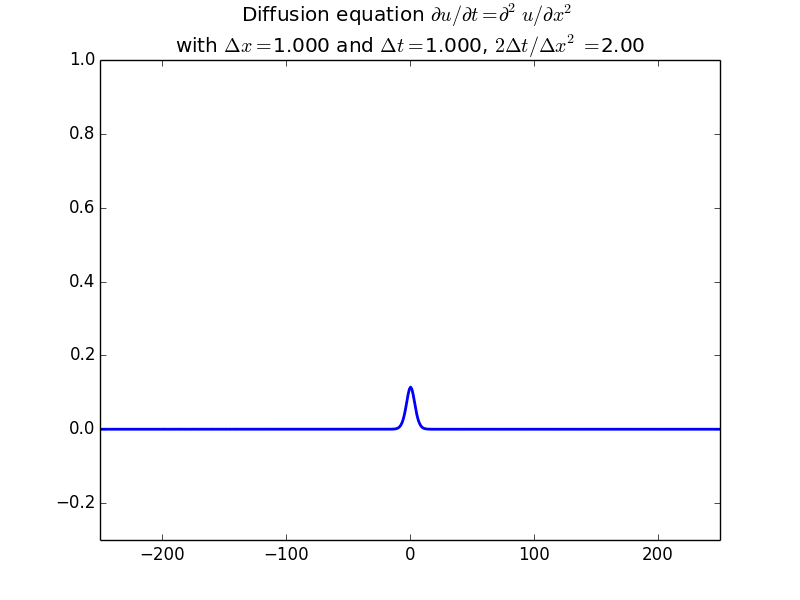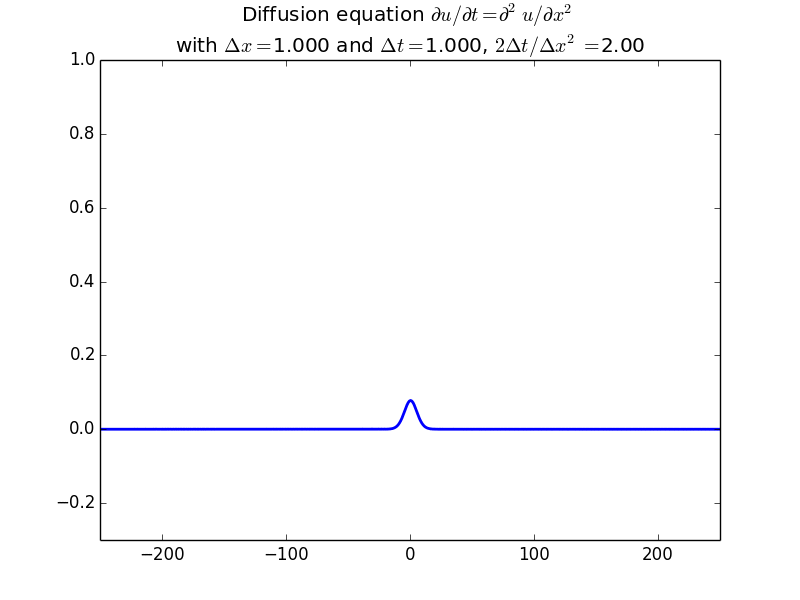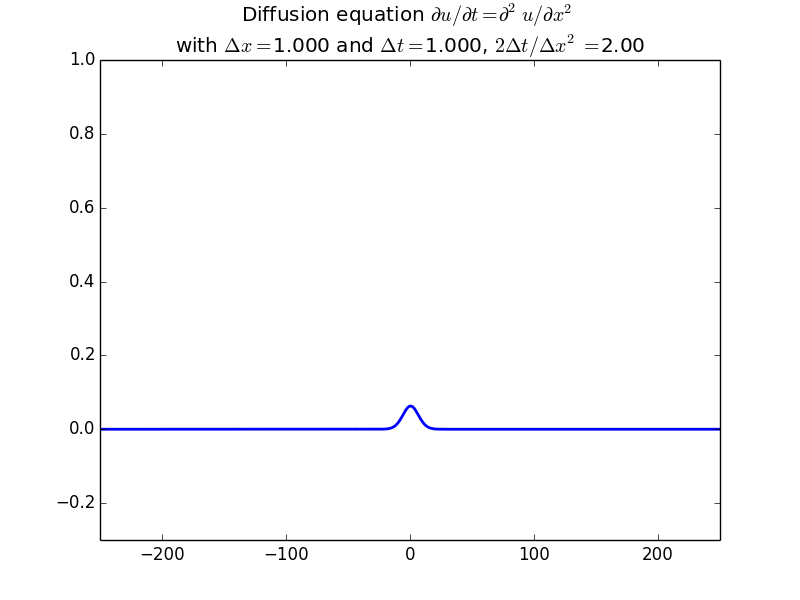
In fact, since the solution should be unconditionally stable, here is the result with another factor of 10 increase in time step:
Use the tridiagonal solver to implement 2d diffusion using the Alternating Direction Implicit method.

python 8.3.py -dt 10. -nx 100 -nt 40 -filename sam-inverted.png

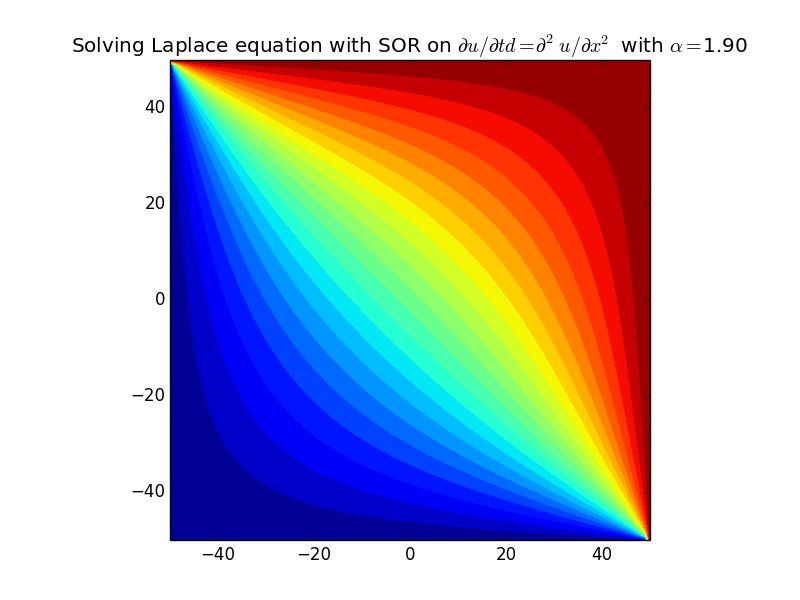
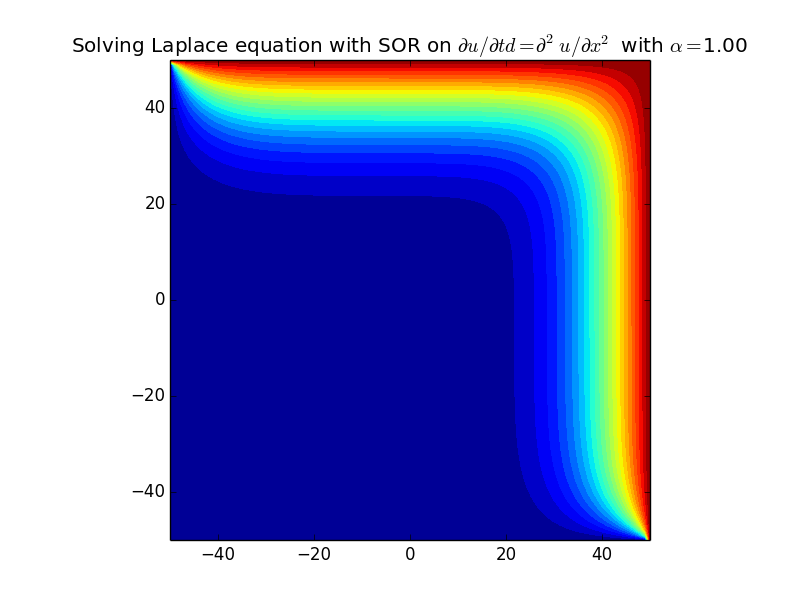
Implement successive over-relaxation with Gauss-Seidel to solve the Laplace equation on a rectangular domain.
python 8.4.py -alpha 1.99 -nt 1000 -nx 100
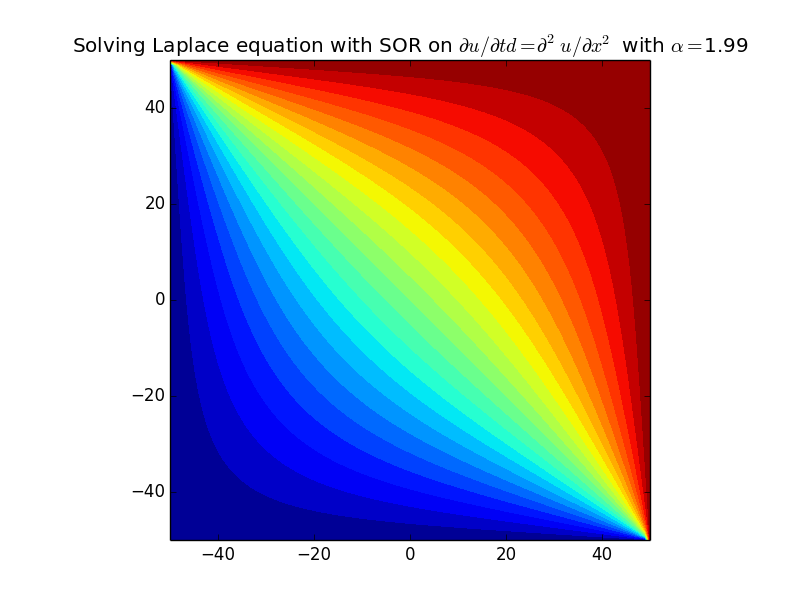
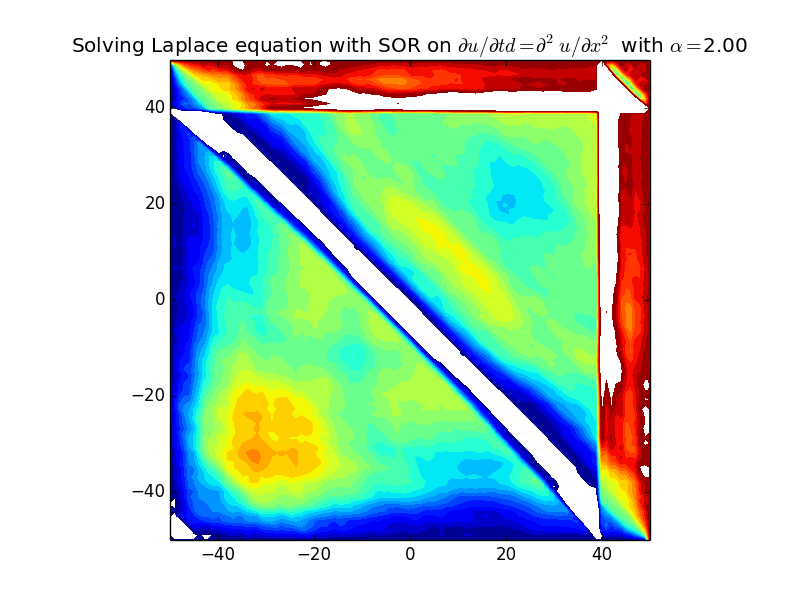
If we take fewer time steps, we can qualitatively compare convergence for stable values of the relaxation parameter.
python 8.4.py -alpha 1.9 -nt 200 -nx 100