Project 9: Transforms
Useful links
- http://snowball.millersville.edu/~adecaria/ESCI386P/esci386-lesson17-Fourier-Transforms.pdf
- http://jakevdp.github.io/blog/2013/08/28/understanding-the-fft/
- http://www.bearcave.com/misl/misl_tech/wavelets/daubechies/index.html
For problem 12.2 I realize I do not know how to tell if I used the Daubechies 4-th order Wavelet correctly! hmm.
code
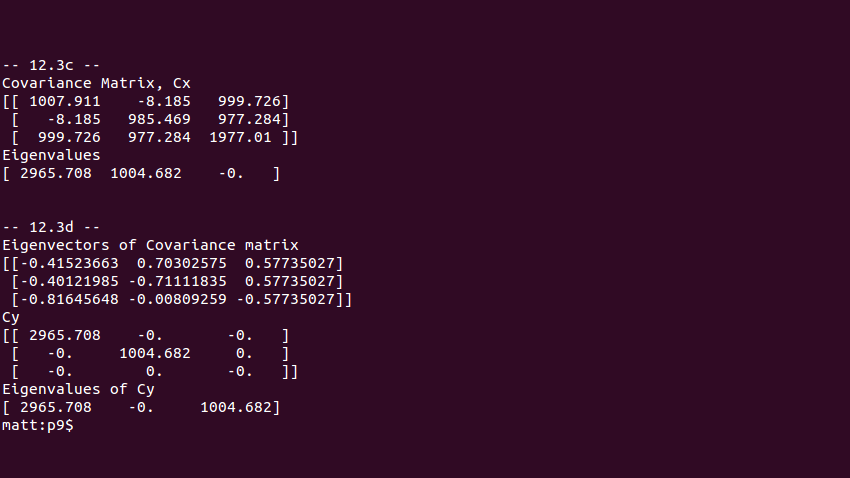
Problems 12.3, analytic solving seemed to get mighty ugly. however the numerical solution was not so ugly. code seemed to work to generate covariance matrix and eigenvalues. I had some trouble for a bit to get a diagonalized matrix until I realized re-read the chapter and saw that the eigenvectors I received from the numpy.linalg.eig(x) function required transposing before using again to calculate the covariance matrix of transformation. The results are shown below.
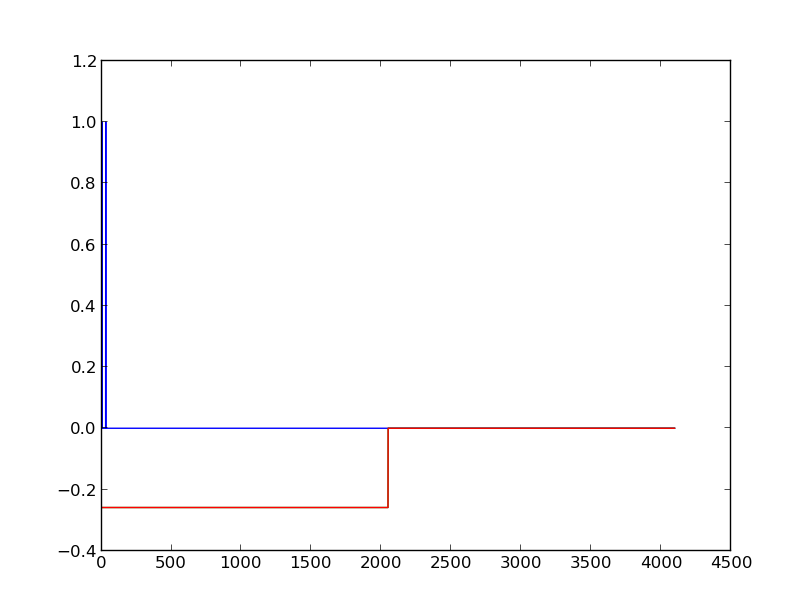
Problems 12.4 Contrast Function. Code generates two streams of data that are uniform random variables contained within [0,1]. We then mix them, remove the mean and diagonalize, and then attempt to identify the independent components using a contrast function.