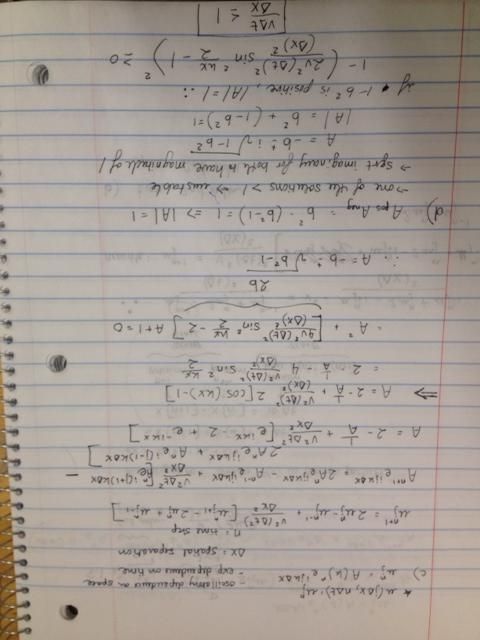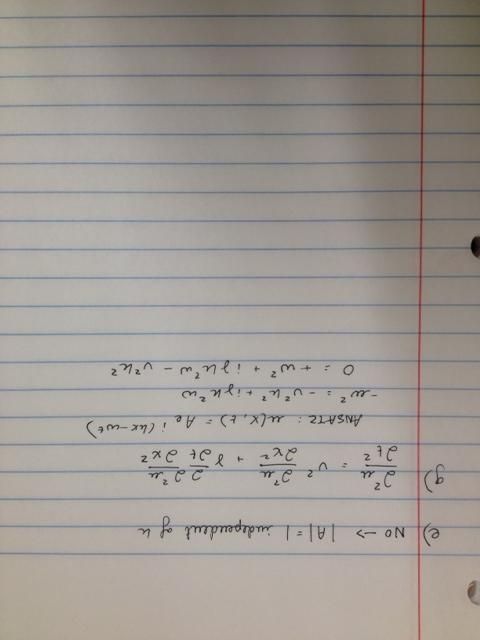Problem Set 5
1D Diffusion Problem: Tridiagonal Matrix Algorithm
This problem set proved mightier than me. While I conceptually understand the mathematics
behind the use of tridiagonal matrices to compute diffusion equation solutions, encoding the
process in Python proved to be pretty difficult. Using C may have been a more intuitive
approach, however I am pretty unfamiliar with C and chose to translate C's logic into python,
rather than learn the C syntax.
Currently, my program is in two pieces:
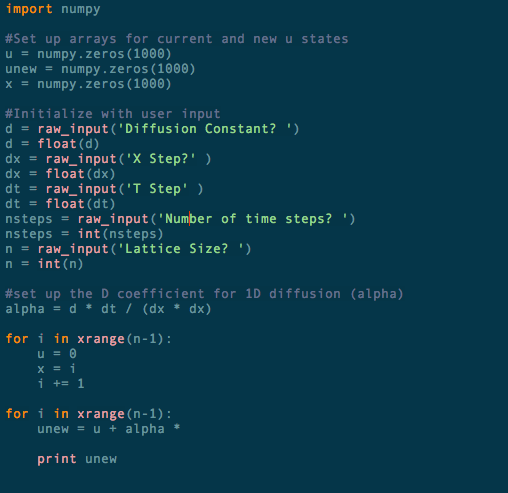
The first intends to compute matrix values using numpy arrays. I begin by setting up arrays for
the current and future function states. I then solicit parameters via raw input from the user. Next, I
condense the diffusion constant dt/(dx)^2 into a single term: alpha. This term is used to update
states in the matrix according to the results of our forward discretization.
My trouble starts with setting up the first array, consisting of 500 sites and the vector needed to
multiply in order to solve for u(sub i, sup n). I can't figure out how to create a tridiagonal matrix in
python that contains different terms of the discretized equation each updated by alpha at the
center state. While I figured out how to set up a tridiagonal matrix in the abstract sense, I had a
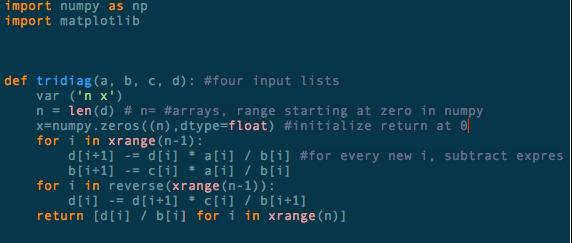
hard time retrofitting it to our specific conditions. The second program piece is this general
tridiagonal matrix.
Below is a screenshot of the current states of my program pieces:
And the general tridiagonal matrix:
Problem Set 5: Handwritten Math Problems
Forward finite-difference approximation:
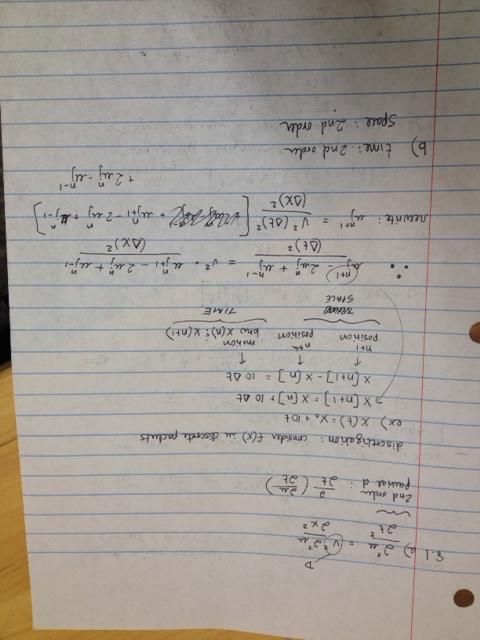
Von Neumann stability and modes of decay: