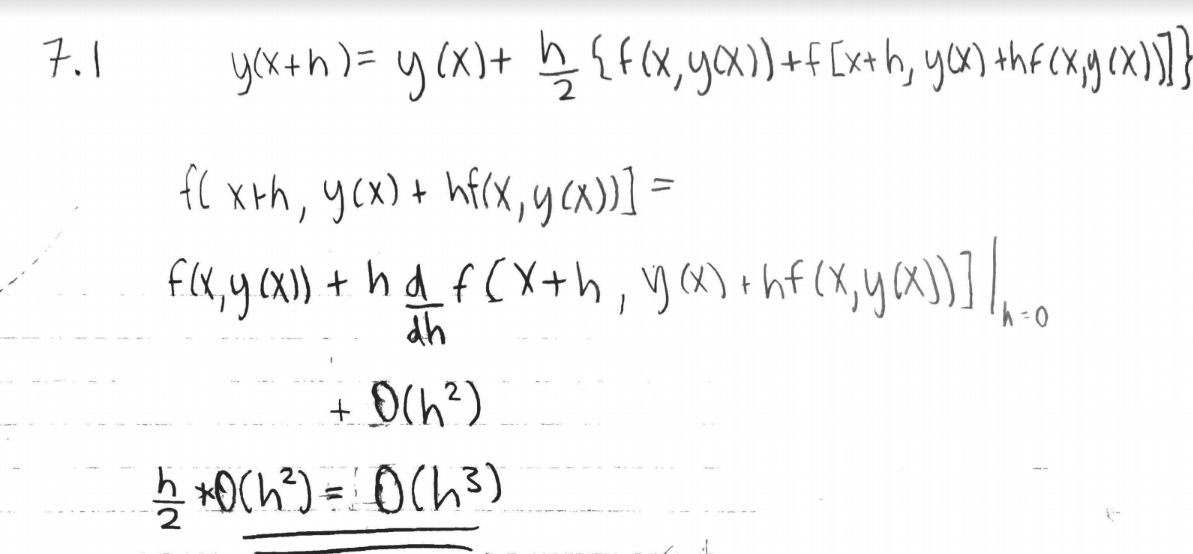
7.2 - Harmonic Oscillator Approximations¶
In [64]:
import matplotlib.pyplot as plt
import numpy as np
%matplotlib notebook
A=np.array([[0, 1],[-1, 0]])
def eulerUpdate(y, h, x):
return y + h*A.dot(y)
def rungeKuttaUpdate(y, h, x):
k1 = h*A.dot(y)
k2 = h*A.dot(y+k1/2.)
k3 = h*A.dot(y+k2/2.)
k4 = h*A.dot(y+k3)
return y+k1/6.+k2/3.+k3/3.+k4/6.
def adaptiveUpdate(y, h, x, maxError, r = 2., N=3):
error = float('inf')
difThreshold = 0.1*maxError
i=1
while True:
f1 = rungeKuttaUpdate(y, h, x)
f2_1 = rungeKuttaUpdate(y, h/2, x)
f2 = rungeKuttaUpdate(f2_1, h/2, x)
error = (f1-f2)[0]
if(abs(error)>maxError):
f3 = rungeKuttaUpdate(rungeKuttaUpdate(y, h/4, x),h/4, x)
error2 = (f2_1-f3)[0]
gradient = (h/2)/abs(error-error2)
else:
if (maxError-abs(error))<difThreshold:
return (f1, h, error)
f2 = rungeKuttaUpdate(f1, h, x)
f3 = rungeKuttaUpdate(y, 2*h, x)
error2 = (f3-f2)[0]
if i>=N:
if abs(error2)>maxError:
return (f1, h, error)
else:
return (f2, 2*h, error)
gradient = (h)/abs(error2-error)
h = h + min(max((abs(error)-maxError)*-gradient*r/i**0.5, -0.95*h),20*h)
i+=1
def localError(y, h, x, f):
f_1 = f(y,h,x)
f_2 = f(f(y, h/2, x), h/2,x)
val = f_1 - f_2
return val[0]
def error(y, x):
return y - np.array([np.cos(x), -np.sin(x)])
def calc(h, update, length=100*np.pi, initial = np.array([1,0])):
vals = np.ndarray((4, int(np.ceil(length/h))))
vals[0, :] = np.arange(0, length, h)
vals[1:3, 0] = initial
vals[3] = 0
x = 0
for i in range(1,vals.shape[1]):
y = vals[1:3, i-1]
vals[1:3,i] = update(y, h, x)
vals[3, i] = localError(y, h, x, update)
x+=h
return vals
def euler(h):
return calc(h, eulerUpdate)
def rungeKutta(h):
return calc(h, rungeKuttaUpdate)
def adaptiveRunge(maxError, initialH=0.001, length=100*np.pi):
h = initialH
vals = np.ndarray((5, 1))
vals[0, 0] = 0
vals[1:3, 0] = np.array([1, 0])
vals[3] = 0
x = 0
i = 1
while x < length:
y = vals[1:3, i-1]
val = np.ndarray(5)
y, h, error = adaptiveUpdate(y, h, x, maxError)
x+=h
val[0] = x
val[1:3] = y
val[3] = error
val[4] = h
vals = np.append(vals, val.reshape((5,1)), axis=1)
i+=1
return vals
def calcPlot(h):
valsEuler = euler(h)
valsRunge = rungeKutta(h)
plt.figure(figsize=(12, 8))
plt.title('Harmonic Oscillation Approximations with h=%f' % h)
cosRange = np.arange(0, 100*np.pi, 0.01)
cosVal = np.cos(cosRange)
plt.plot(cosRange, cosVal, label='System')
plt.plot(valsRunge[0,:], valsRunge[1,:], label='Runge-Kutta approximation')
plt.plot(valsEuler[0,:], valsEuler[1,:], label='Euler approximation')
plt.legend()
plt.ylim((-2,2))
plt.xlim((0,100*np.pi))
plt.show()
eulerError = error(valsEuler[1:3,-1], valsEuler[0,-1])
rungeError = error(valsRunge[1:3,-1], valsRunge[0,-1])
print(("Euler Error\n"
"=====\n"
"Mean abs local error:\t%f\n"
"Final value error:\t%f\n"
"Final slope error:\t%f\n"
"\n"
"Runge-Kutta Error\n"
"=====\n"
"Mean abs local error:\t%f\n"
"Final value error:\t%f\n"
"Final slope error:\t%f"
) % (np.mean(np.absolute(valsEuler[3,:])), eulerError[0], eulerError[1], np.mean(np.absolute(valsRunge[3,:])),rungeError[0],rungeError[1])
)
#plt.figure(figsize=(12, 8))
#plt.title('Errors over Harmonic Oscillation with Adaptive Approximations')
#plt.plot(valsRunge[0,:],valsRunge[3,:], label='local Error')
#plt.legend()
#plt.show()
def calcAdaptivePlot(maxError):
vals = adaptiveRunge(maxError)
plt.figure(figsize=(12, 8))
plt.title('Harmonic Oscillation Adaptive Approximations with maxError=%f' % maxError)
cosRange = np.arange(0, 100*np.pi, 0.01)
cosVal = np.cos(cosRange)
plt.plot(cosRange, cosVal, label='System')
plt.plot(vals[0,:], vals[1,:], label='Adaptive Runge-Kutta')
plt.legend()
plt.ylim((-2,2))
plt.xlim((0,100*np.pi))
plt.show()
rungeError = error(vals[1:3,-1], vals[0,-1])
print(("Runge-Kutta Error\n"
"=====\n"
"Mean abs local error:\t%f\n"
"Final value error:\t%f\n"
"Final slope error:\t%f\n"
"Mean h:\t%f\n"
) % (np.mean(np.absolute(vals[3,:])),rungeError[0],rungeError[1], np.mean(vals[4,:]))
)
plt.figure(figsize=(12, 8))
plt.title('h over Harmonic Oscillation with Adaptive Approximations')
plt.plot(vals[0,:],vals[4,:], label='h')
plt.ylim((0,1))
plt.xlim((0,100*np.pi))
plt.legend()
plt.show()
plt.figure(figsize=(12, 8))
plt.title('Local Error Magnitudes over Harmonic Oscillation with Adaptive Approximations')
plt.plot((0, 100*np.pi), (maxError, maxError), 'red', label='maxError')
plt.plot(vals[0,:],np.absolute(vals[3,:]), label='local Error')
plt.ylim((0,2*maxError))
plt.xlim((0,100*np.pi))
plt.legend()
plt.show()
In [20]:
calcPlot(0.0001)
In [19]:
calcPlot(0.01)
In [18]:
calcPlot(1)
7.3 - Adaptive Harmonic Oscillation Approximations¶
In [21]:
calcAdaptivePlot(0.001)
Comparison to Non-Adaptive with h = mean(h) of Adaptive System¶
In [22]:
calcPlot(0.745)
7.4¶
In [288]:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from ipywidgets import interact
%matplotlib notebook
class pendulum:
def __init__(self, l, w, A, h=0.002, initial=None, g=9.8):
self.l=l
self.g=g
self.h=h
self.w=w
self.A=A
self.x=0
if initial==None:
initial = np.array([np.pi/5, 0])
self.y=initial
def pendulumGradient(self, y, x):
z_accel = self.w**2*self.A*np.sin(self.w*x)
return np.array([y[1], (-self.g-z_accel)*np.sin(y[0])/self.l])
def pendulumUpdate(self):
self.x+=self.h
k1 = self.h*self.pendulumGradient(self.y, self.x)
k2 = self.h*self.pendulumGradient(self.y+k1/2., self.x+self.h/2.)
k3 = self.h*self.pendulumGradient(self.y+k2/2.,self.x+self.h/2.)
k4 = self.h*self.pendulumGradient(self.y+k3, self.x+self.h)
self.y+=k1/6.+k2/3.+k3/3.+k4/6.
return self.y
def linePoints(self):
return ([1,1+self.l*np.sin(self.y[0])], [1,1-self.l*np.cos(self.y[0])])
def animate(i):
global p
p.pendulumUpdate()
lineX, lineY = p.linePoints()
line.set_data(lineX, lineY) # update the data
line.set_data(lineX, lineY)
dot.set_data(lineX[1], lineY[1])
time_text.set_text(str(i*p.h))
return line, dot
In [279]:
l=1
w=3
A=3
p = pendulum(1, 2, 3)
lineX, lineY = p.linePoints()
fig, ax = plt.subplots()
plt.ylim((-1,1))
plt.xlim((0,2))
line, = ax.plot(lineX, lineY)
dot, = ax.plot(lineX[1], lineY[1], 'ro', markersize=20)
text = ax.text(.1, .9, 'w=%f, A=%f'%(w,A), fontsize=15)
time_text = ax.text(.1, .75, 'what', fontsize=15)
ani = animation.FuncAnimation(fig, animate, np.arange(1, 5000), interval=2)
plt.show()
#interact(run, A=(0,20,.1), w=(0,10,.1))
#vals = calc(h, pendulumUpdate, initial=np.array([0,0]))
In [296]:
l, w, A = (1,2,3)
p2 = pendulum(l,w,A)
print p2.y
time = np.arange(0, 100, 0.002)
y = [p2.pendulumUpdate()[0] for t in time]
plt.figure()
plt.title("Theta over time for pendulum with l=%f, zW=%f, zA=%f" % (l,w,A))
plt.plot(time, y)
plt.ylim(-np.pi, np.pi)
print y[:3]
In [147]:
In [151]:
In [ ]: