Ordinary Differential and Difference Equations

Week 2

Link to completed assignment

Problem 3.1

(a) The conditions that allow for simple undamped harmonic motion are when there are no outside forces of friction or gravity being accounted for or affecting the system.

(b) See image below for the homogeneous solution to the problem. Note that the amplitude does not depend on frequency.

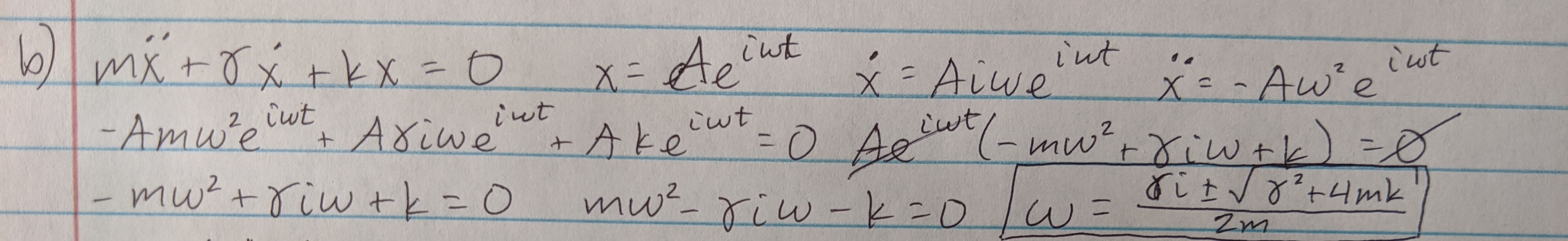
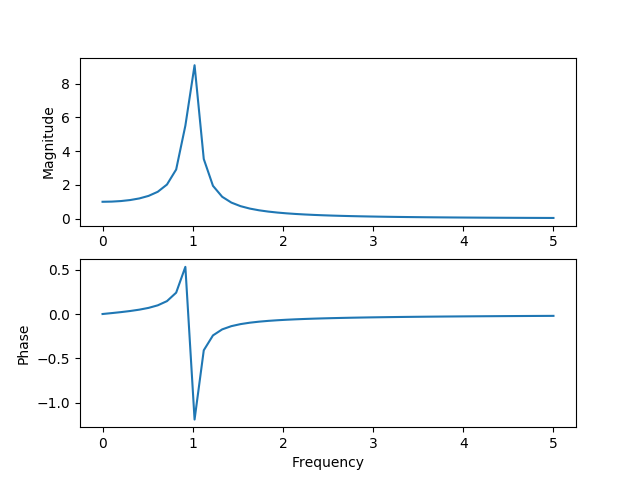
(c) Here is the particular solution to the inhomogeneous problem, followed by the plot for its magnitude and phase (plotted using numpy and matplotlib in Python).

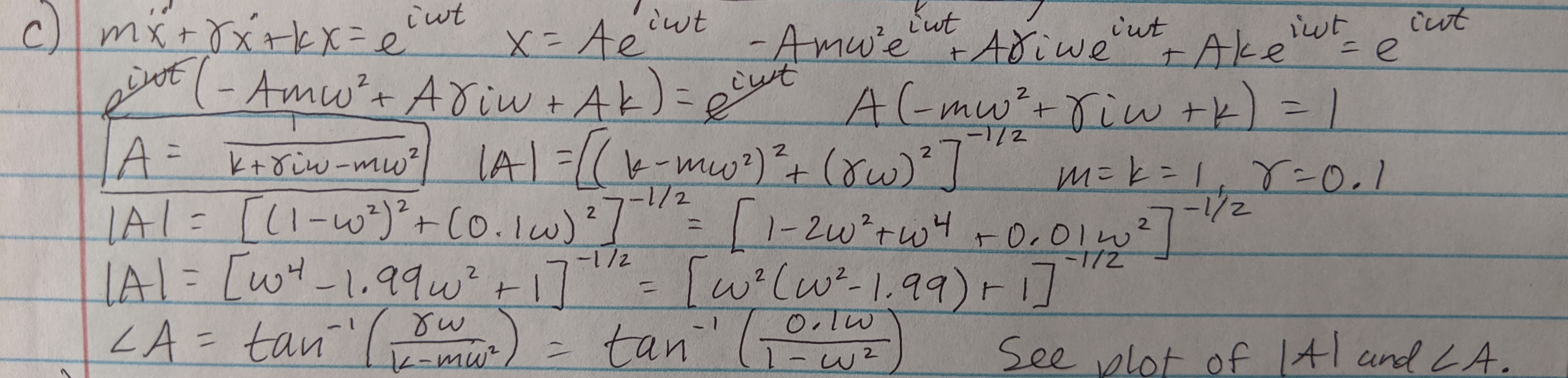
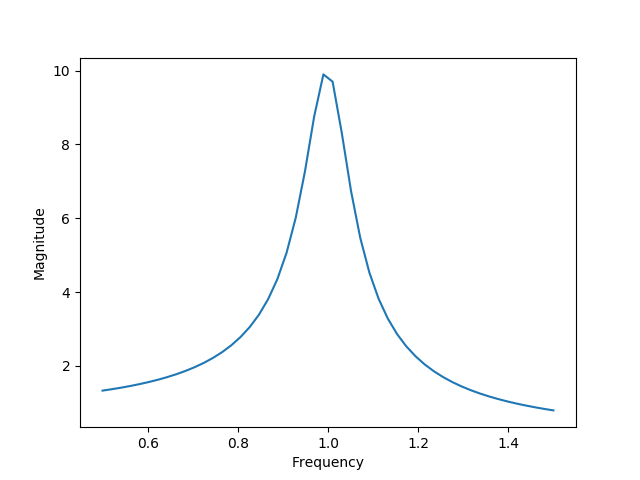
(d) To find the Q factor, I know that it is the ratio of the center frequency to the width of the curve where the magnitude drops to half of its maximum, so looking at the plot from above zoomed in (see below), we can see that the center frequency is right around 1 rad/s, then the width of the curve is about 0.2 rad/s. This gives us a Q factor of 5. I was unable to get much farther with this solution as I floundered, unfortunately.

(e) I made it through using Laplace transforms quite far until I encountered a pretty complex fraction in the Laplace domain. I tried taming it, but am not sure that I got it right since it doesn't quite match with previous solutions obtained using other methods.

(f) I skipped this portion so I could focus on solving the next two problems since it wasn't as obvious as to how I'd approach it.

Problem 3.2

After reviewing some notes from my ODE class from undergrad, I was able to remember how to derive the equations of motion for the system, which was necessary to set up the system of equations for this problem and then simplify it. You can see those below. I floundered quite a bit determining how to put everything into a matrix so I could diagonalize it, but didn't figure it out.

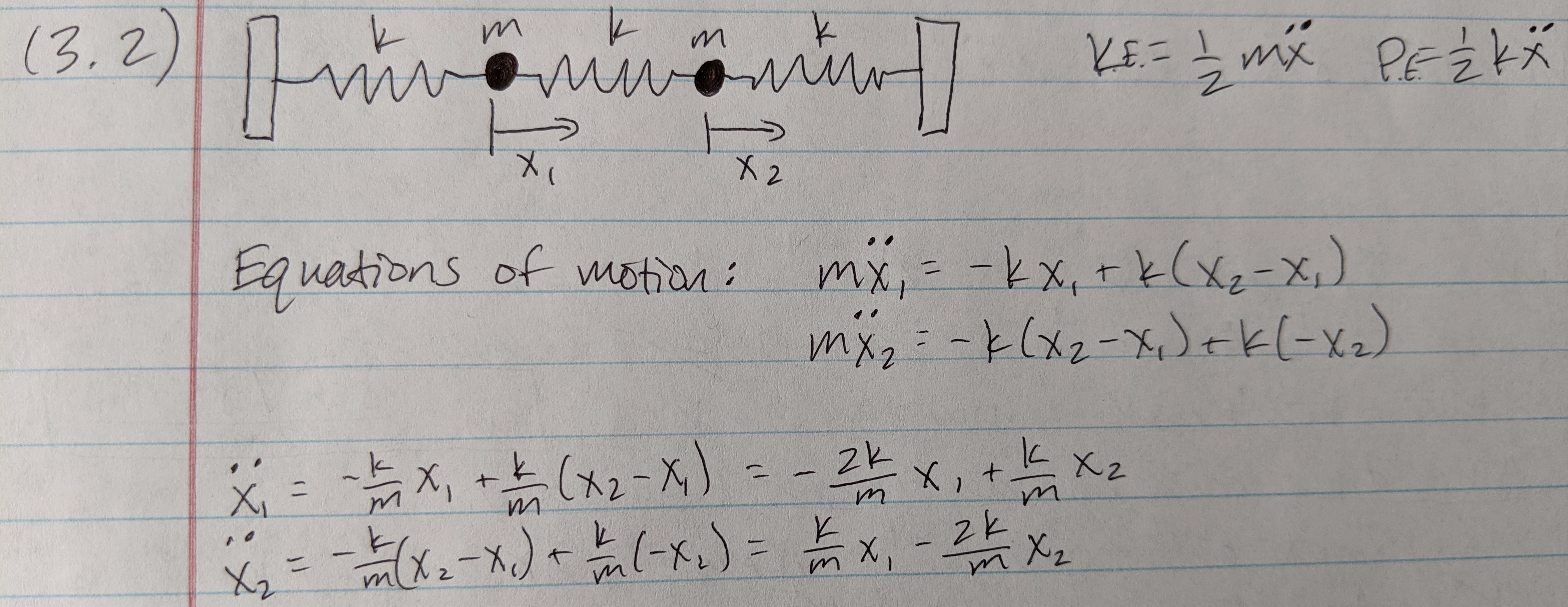
Problem 3.3

This was another problem that I did the little bit that I could immediately decipher before going back to read more. I just didn't start early enough to have time to get through this problem. Below is what I did to start the problem.

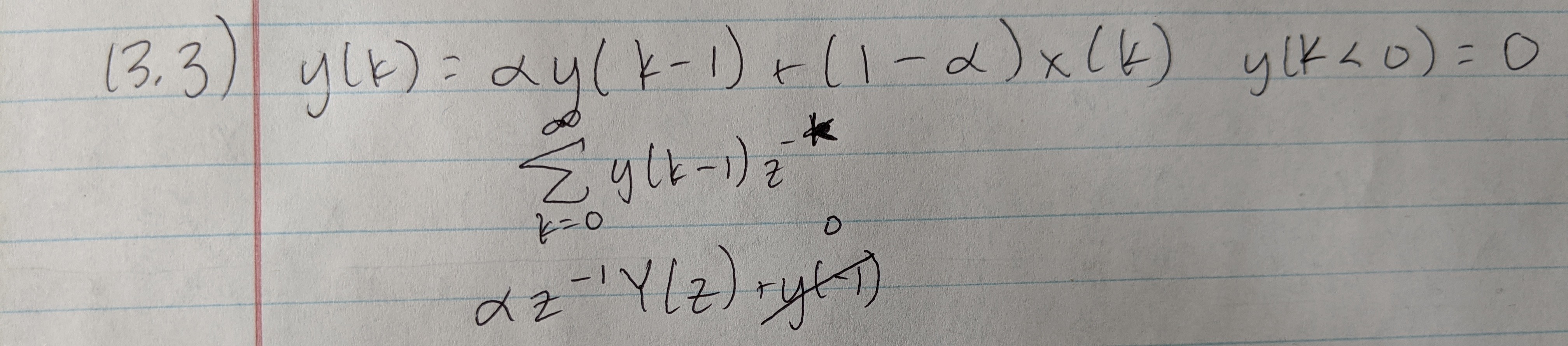
I should have started much earlier with this assignment so I could have asked better questions during the TA session and so that there would still be enough time to flounder, yet complete the problems all before class. That has been noted and I will be sure to start earlier from now on.