Random Systems
Week 3
Link to completed assignment
Problem 6.1
Problem 6.1
(a) Using Equations 6.24-6.26 from the textbook, I was able to expand and solve both sides, paying attention only to terms with k terms of the first, second, and third orders for the first three cumulants. Note that the first cumulant is the mean and the second cumulant is the variance.
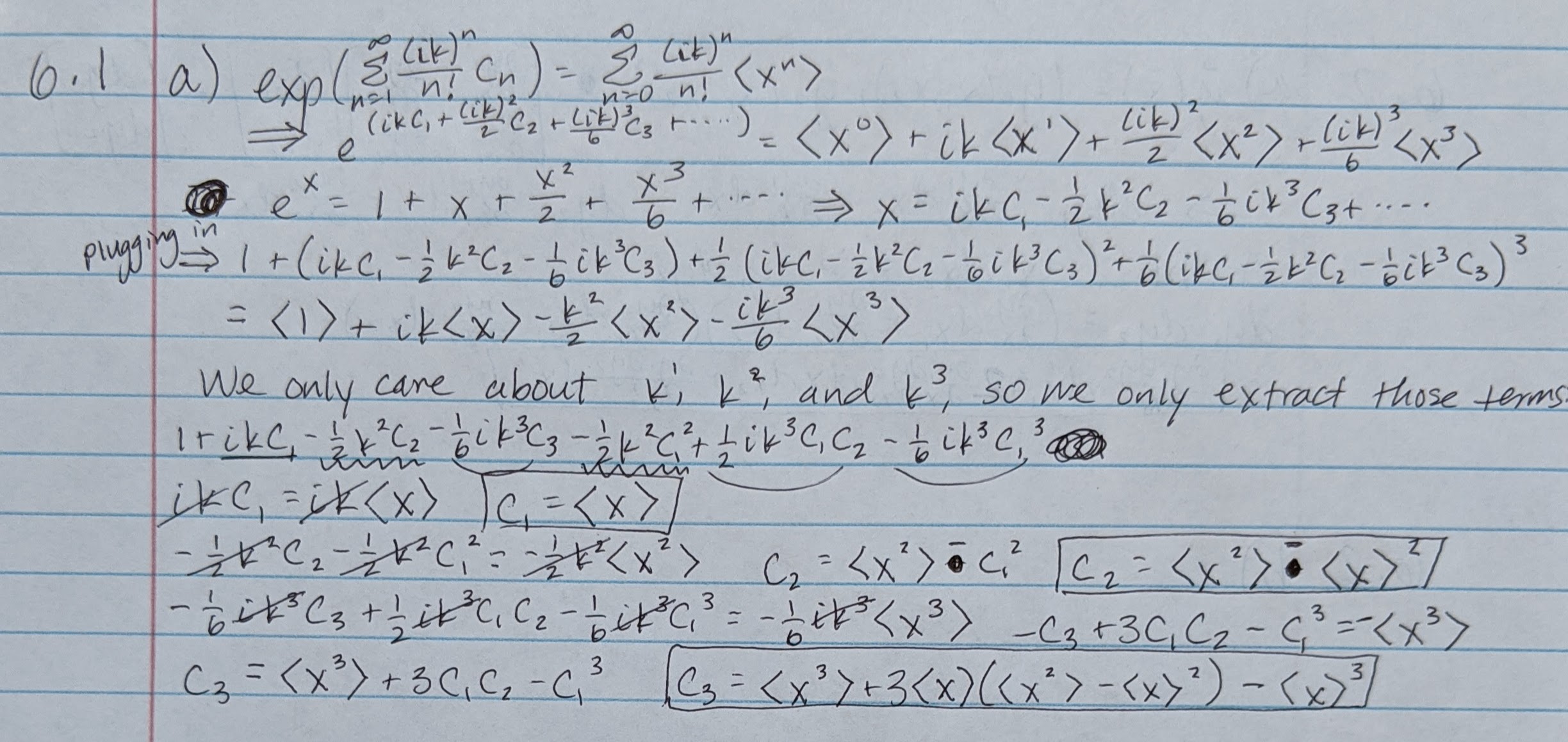
(b) While the integral might look nasty, I remembered from a previous class that the mean and variance of a Gaussian distribution are known and simply represented by symbols μ and σ2. This helped me simplify, but I wasn't quite able to solve completely for the third cumulant.
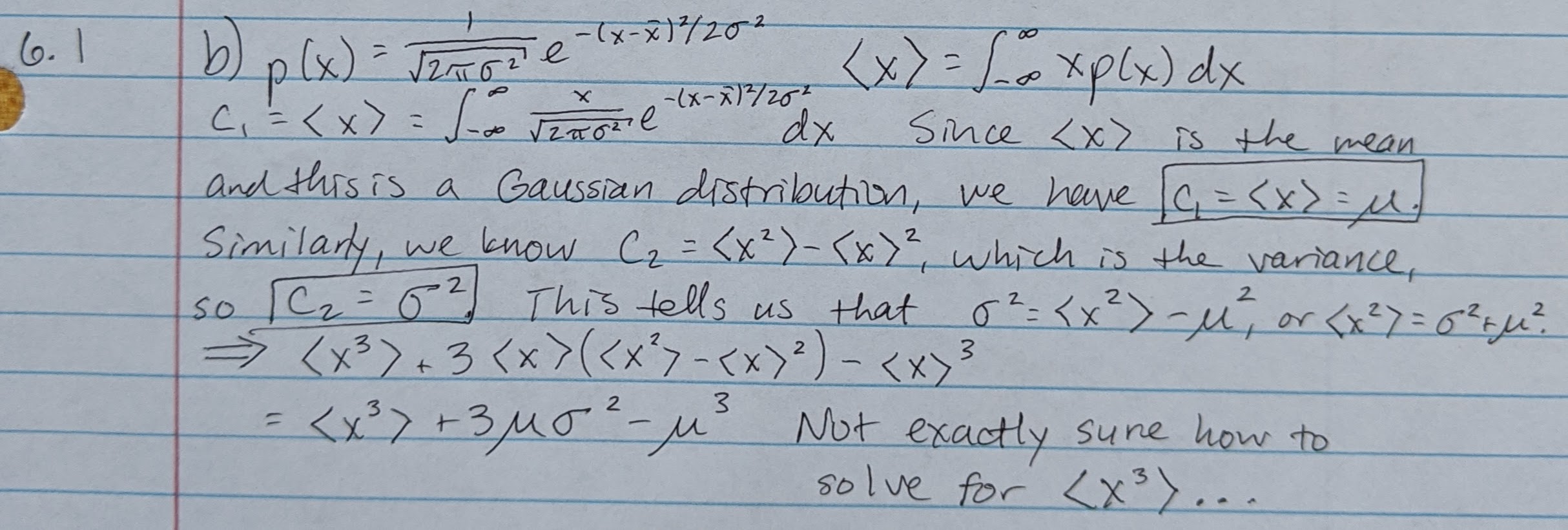
Problem 6.2
(a) Knowing that the area of the parallelogram is equal to the base times the height gives us a hint that after mapping dx1 dx2, the area will just be dy1 times dy2.
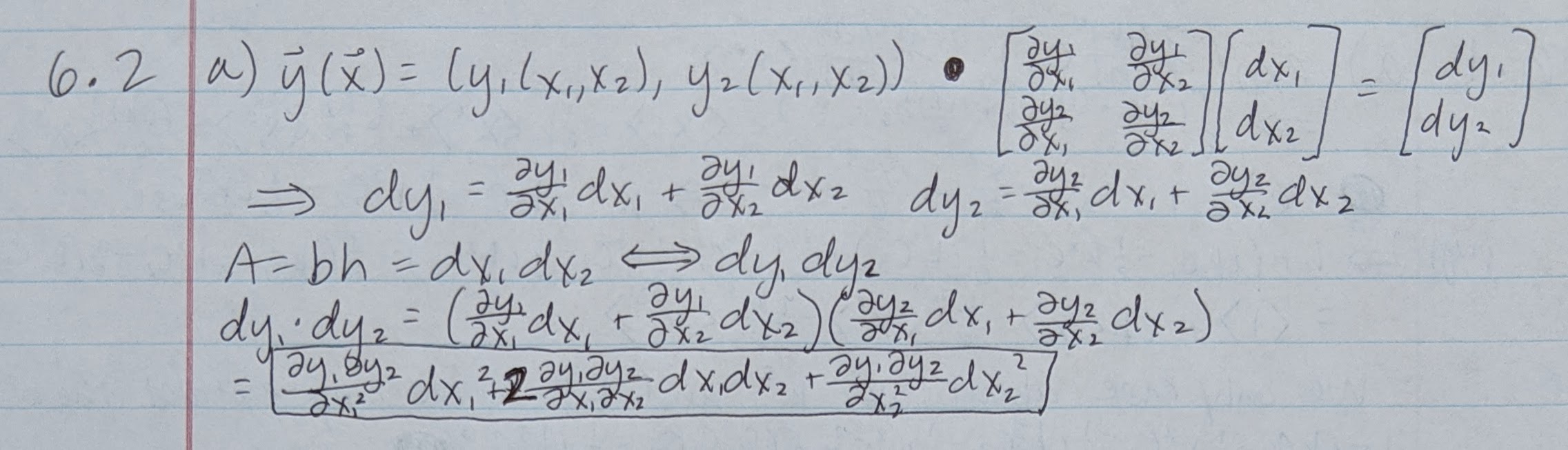
(b)
(c)
Problem 6.3
(a) Using Table 6.1 from the textbook, I knew that an order 4 maximal LFSR had i values of 1 and 4. Knowing this, each successive value would be determined by the logic equation xn-1 ^ xn-4. I used "1111" as my seed value, and proceeded to fill out the bit sequence.

(b) Knowing that the number of total possible patterns is just two to the power of the number of bits, as well as knowing that the number of patterns divided by the clock rate in Hz gives us the total time in seconds between repeats in the pattern helped me set up this equation. Note that while the final answer was closer to 88 bits, you need 89 bits if you don't want to repeat before the given time interval.

Problem 6.4
(a)
(b)
(c)
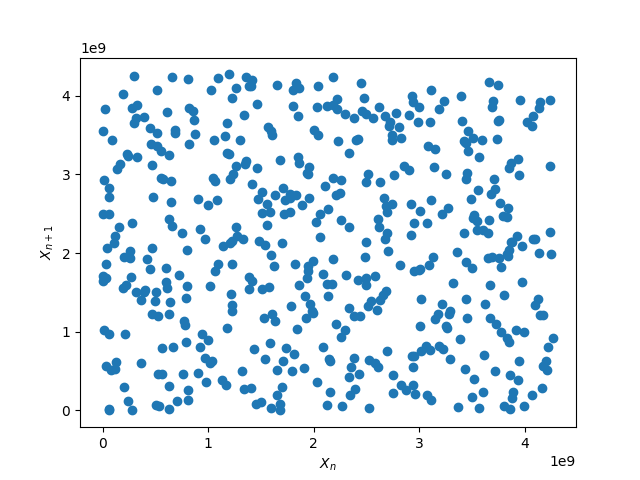
(d) Using the recommended Linear Congruential Generator (LCG) as suggested in class, I was able to simulate 10 trajectories of a random 1D walker. I used suggested values from Wikipedia for the best possible LCG. Those values are a = 1103515245, c = 12345, m = 232. The plot of this LCG's distribution, as well as the random 1D walker trajectories are below.
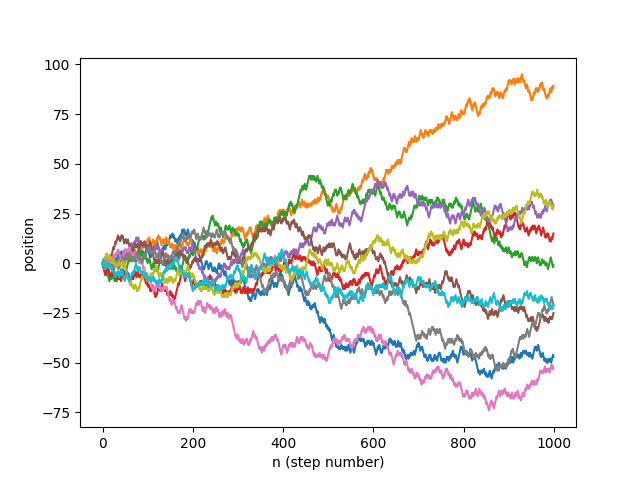
(e)