Finite Differences: Ordinary Differential Equations
Week 4
Link to completed assignment
Problem 7.1
Problem 7.1
After going through and expanding the equation given in the problem and solving it, we can see that it is identical to the actual Taylor expansion of the problem, and therefore there is no difference in the first terms, and the error lies in the other higher terms, giving us an error of O(h3). Note that in the image below, in the final line, I forgot to insert a df/dy term next to the f(x,y(x)) term in the final set of parentheses.
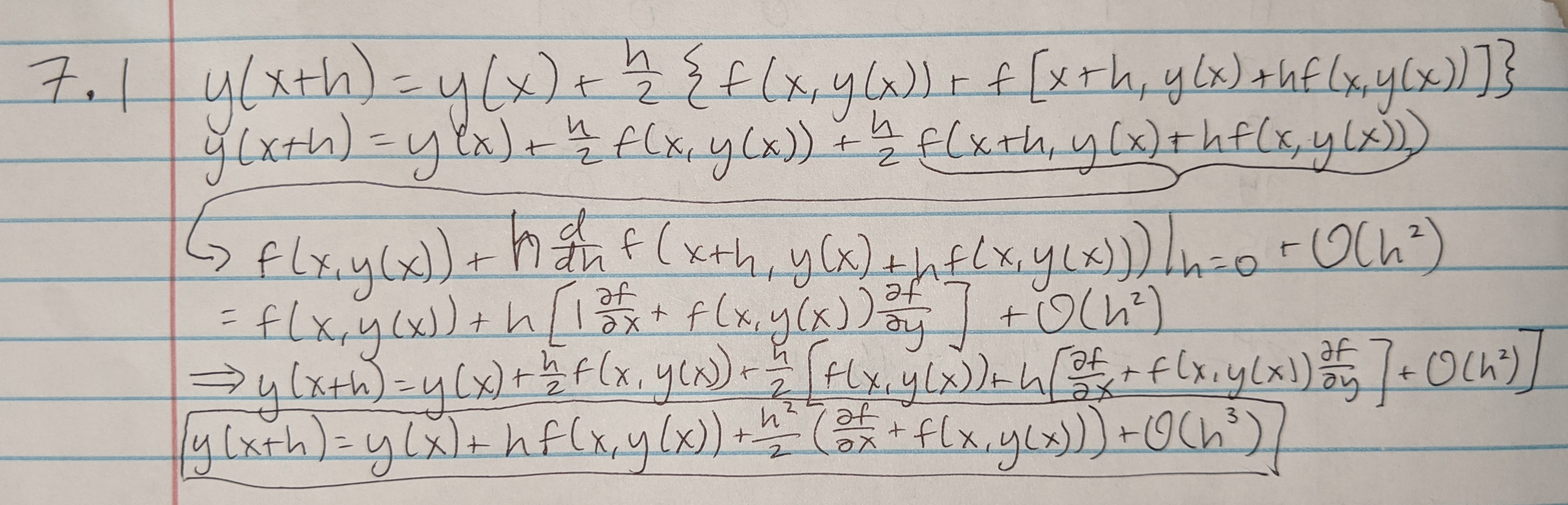
Problem 7.2
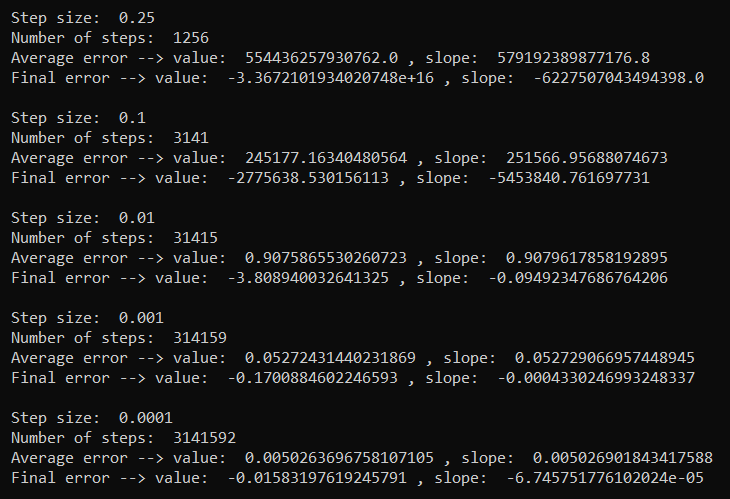
First, I solved for how to actually set up the equation in terms of two different y terms, one being y, and the other being y'. I then used the following code to implement it using the Euler method. The results of the method are shown below the code.
import matplotlib.pyplot as plt
import numpy as np
print()
steps = [0.25, 0.1, 0.01, 0.001, 0.0001]
for h in steps:
y1 = [1.0]
y2 = [0.0]
t_max = 100*np.pi
num_steps = int(t_max/h)
t = np.linspace(0,t_max,num_steps)
y1_exact = np.cos(t)
y2_exact = -np.sin(t)
value_error = []
slope_error = []
value_error_total = 0.0
slope_error_total = 0.0
for i in range(num_steps):
y1_ = y1[i] + h*y2[i]
y2_ = y2[i] - h*y1[i]
y1.append(y1_)
y2.append(y2_)
val_err = np.absolute(y1_exact[i] - y1[i])
slo_err = np.absolute(y2_exact[i] - y2[i])
value_error.append(val_err)
slope_error.append(slo_err)
value_error_total += val_err
slope_error_total += slo_err
value_error_final = (y1_exact[len(y1_exact)-1] - y1[len(y1)-1])
slope_error_final = (y2_exact[len(y2_exact)-1] - y2[len(y2)-1])
value_error_average = value_error_total / (len(value_error)-1)
slope_error_average = slope_error_total / (len(slope_error)-1)
print("Step size: ", h)
print("Number of steps: ", len(y1)-1)
print("Average error --> value: ", value_error_average, ", slope: ", slope_error_average)
print("Final error --> value: ", value_error_final, ", slope: ", slope_error_final)
print()
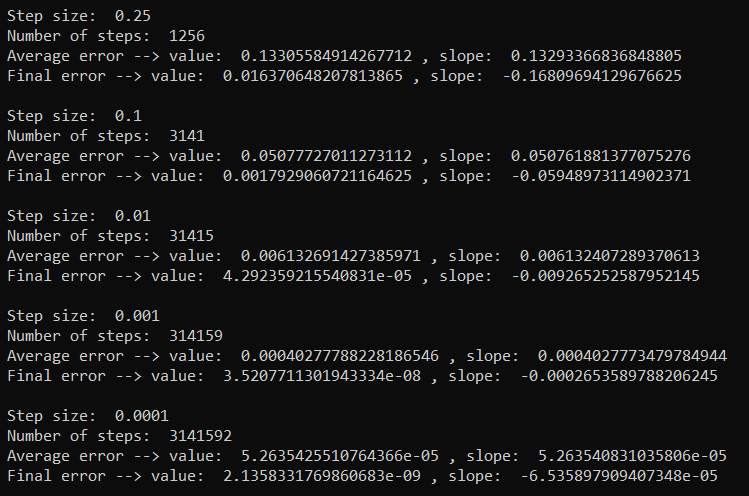
Next, I implemented the same function using the fourth-order Runge-Kutta method. It was a little more complex to set up, but the error is significantly decreased using this method over the Euler method for all step sizes.
import matplotlib.pyplot as plt
import numpy as np
print()
steps = [0.25, 0.1, 0.01, 0.001, 0.0001]
for h in steps:
y1 = [1.0]
y2 = [0.0]
t_max = 100*np.pi
num_steps = int(t_max/h)
t = np.linspace(0,t_max,num_steps)
y1_exact = np.cos(t)
y2_exact = -np.sin(t)
value_error = []
slope_error = []
value_error_total = 0.0
slope_error_total = 0.0
for i in range(num_steps):
k1_y1 = h * y2[i]
k1_y2 = -h * y1[i]
k2_y1 = h * (y2[i] + k1_y2/2)
k2_y2 = -h * (y1[i] + k1_y1/2)
k3_y1 = h * (y2[i] + k2_y2/2)
k3_y2 = -h * (y1[i] + k2_y1/2)
k4_y1 = h * (y2[i] + k3_y2)
k4_y2 = -h * (y1[i] + k3_y1)
y1_ = y1[i] + (k1_y1/6) + (k2_y1/3) + (k3_y1/3) + (k4_y1/6)
y2_ = y2[i] + (k1_y2/6) + (k2_y2/3) + (k3_y2/3) + (k4_y2/6)
y1.append(y1_)
y2.append(y2_)
val_err = np.absolute(y1_exact[i] - y1[i])
slo_err = np.absolute(y2_exact[i] - y2[i])
value_error.append(val_err)
slope_error.append(slo_err)
value_error_total += val_err
slope_error_total += slo_err
value_error_final = (y1_exact[len(y1_exact)-1] - y1[len(y1)-1])
slope_error_final = (y2_exact[len(y2_exact)-1] - y2[len(y2)-1])
value_error_average = value_error_total / (len(value_error)-1)
slope_error_average = slope_error_total / (len(slope_error)-1)
print("Step size: ", h)
print("Number of steps: ", len(y1)-1)
print("Average error --> value: ", value_error_average, ", slope: ", slope_error_average)
print("Final error --> value: ", value_error_final, ", slope: ", slope_error_final)
print()
Problem 7.3
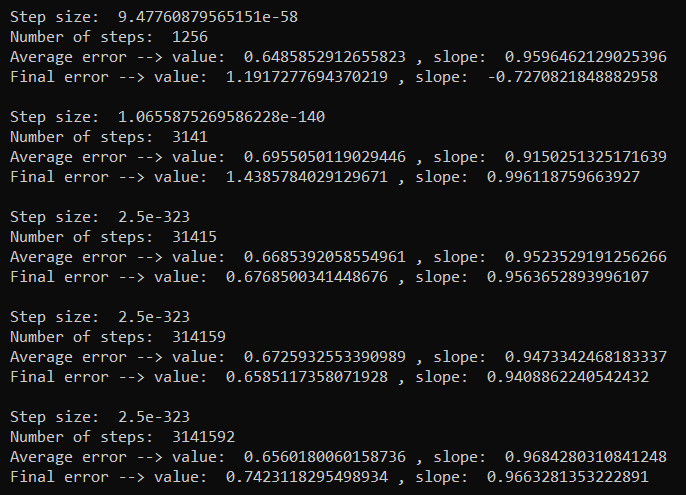
I then set out to adapt my Runge-Kutta algorithm to adapt the step size depending on the desired error. I remember learning in class that it was fairly easy to implement, with the central idea being if the error is greater than the desired error, lower the step size, and if not, increase the step size to be more efficient. I tried a couple of different methods, but my code just continued to decrease the step size to incredibly small values, making it run forever, without giving me the intended results. Here are my efforts with the very wrong results from what is expected:
import matplotlib.pyplot as plt
import numpy as np
print()
error_min = 0.05
error_max = 0.10
steps = [0.25, 0.1, 0.01, 0.001, 0.0001]
for h in steps:
y1 = [1.0]
y2 = [0.0]
t_max = 100*np.pi
num_steps = int(t_max/h)
t = np.linspace(0,t_max,num_steps)
y1_exact = np.cos(t)
y2_exact = -np.sin(t)
value_error = []
slope_error = []
value_error_pct = 0.0
slope_error_pct = 0.0
value_error_total = 0.0
slope_error_total = 0.0
for i in range(num_steps - 1):
k1_y1 = h * y2[i]
k1_y2 = -h * y1[i]
k2_y1 = h * (y2[i] + k1_y2/2)
k2_y2 = -h * (y1[i] + k1_y1/2)
k3_y1 = h * (y2[i] + k2_y2/2)
k3_y2 = -h * (y1[i] + k2_y1/2)
k4_y1 = h * (y2[i] + k3_y2)
k4_y2 = -h * (y1[i] + k3_y1)
y1_ = y1[i] + (k1_y1/6) + (k2_y1/3) + (k3_y1/3) + (k4_y1/6)
y2_ = y2[i] + (k1_y2/6) + (k2_y2/3) + (k3_y2/3) + (k4_y2/6)
y1.append(y1_)
y2.append(y2_)
val_err = np.absolute(y1_exact[i] - y1[i])
slo_err = np.absolute(y2_exact[i] - y2[i])
value_error.append(val_err)
slope_error.append(slo_err)
value_error_total += val_err
slope_error_total += slo_err
if y1_exact[i] != 0.0:
value_error_pct = np.absolute(val_err / y1_exact[i])
if y2_exact[i] != 0.0:
slope_error_pct = np.absolute(slo_err / y2_exact[i])
if (value_error_pct > error_max) or (slope_error_pct > error_max):
h = h * 0.9
elif (value_error_pct < error_min) or (slope_error_pct < error_min):
h = h * 1.1
value_error_final = (y1_exact[num_steps-2] - y1[num_steps-2])
slope_error_final = (y2_exact[num_steps-2] - y2[num_steps-2])
value_error_average = value_error_total / num_steps
slope_error_average = slope_error_total / num_steps
print("Step size: ", h)
print("Number of steps: ", num_steps)
print("Average error --> value: ", value_error_average, ", slope: ", slope_error_average)
print("Final error --> value: ", value_error_final, ", slope: ", slope_error_final)
print()
Problem 7.4