Function Fitting
Week 7
Link to completed assignment
Problem 12.1
Problem 12.1
First, we need to use an SVD to fit y = a + bx to our data set.
import matplotlib.pyplot as plt
from sympy import *
import numpy as np
import numpy.linalg as la
x = np.random.uniform(0.0,1.0,100)
zeta = np.random.normal(0.0,0.5,100)
y = 2 + 3*x + zeta
def fit_svd(x, y):
A = np.zeros((100,2))
for i in range(0,100):
A[i][0] = 1
A[i][1] = x[i]
U, w, VT = la.svd(A)
w_diag = np.diag(w)
w_inv = la.inv(w_diag)
w_inverse = np.zeros((2,100))
w_inverse[0][0] = w_inv[0][0]
w_inverse[1][1] = w_inv[1][1]
UT = np.transpose(U)
V = np.transpose(VT)
temp1 = V.dot(w_inverse)
temp2 = temp1.dot(UT)
fit = temp2.dot(y)
return fit
a, b = fit_svd(x, y)
y_new = a + b*x
plt.scatter(x, y, color='red')
plt.plot(x, y_new, color='blue')
plt.savefig('./plots/function_fitting.png')
Which gives us the following plot:
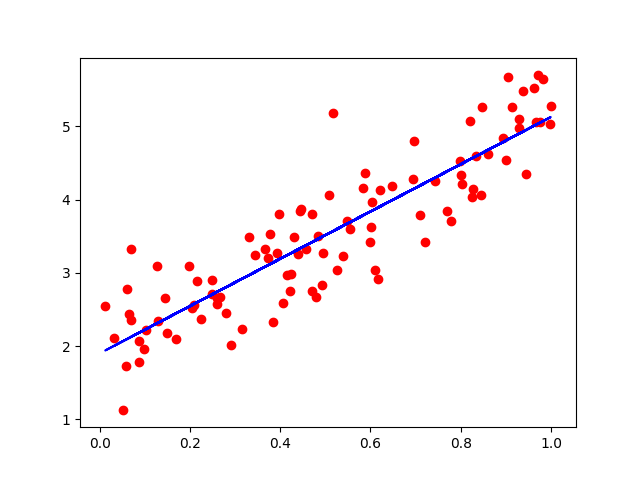
(a) Next, we need to evaluate the error in a and b using Equation (12.34).
A = np.zeros((100,2))
for i in range(0,100):
A[i][0] = 1
A[i][1] = x[i]
U, w, VT = la.svd(A)
error = np.sum(VT**2/w, axis=1)
print()
print(error[0], error[1])
Which gives us values of 0.15668638 and 0.31930671.
(b) Next, we want to use the bootstrap approach generating 100 data sets to evaluate the error.
i = np.linspace(0, 99, 100).astype(int)
A, B = [], []
for _ in range(100):
rand = np.random.choice(i, 100)
x_rand, y_rand = x[rand], y[rand]
a, b = fit_svd(x_rand, y_rand)
A.append(a)
B.append(b)
print(np.var(A), np.var(B))
Which gives us values of 0.01069758 and 0.02890311.
(c) Finally, we want to fit an ensemble of 100 independent data sets to evaluate the error.
A, B = [], []
for _ in range(100):
x = np.random.uniform(0.0, 1.0, 100)
zeta = np.random.normal(0.0, 0.5, 100)
y = 2 + 3*x + zeta
a, b = fit_svd(x, y)
A.append(a)
B.append(b)
print(np.var(A), np.var(B))
Which gives us values of 0.01165382 and 0.03054790.
Problem 12.2