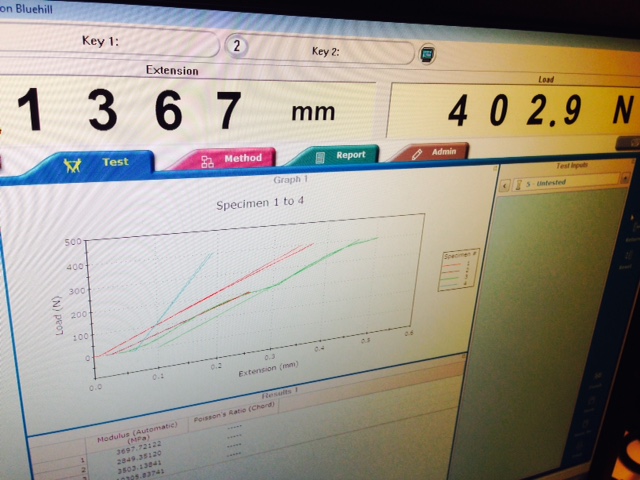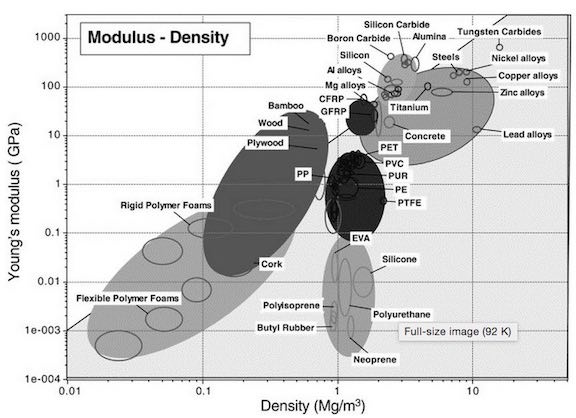
This week, we have an interesting assignment of measuring the stiffness and strength of materials that we would like to try out as samples. Taking a stab at the readings, I learned of the importance of understanding the various properties of the materials and what they can be used for. It is extremely important for the designer or engineer to consider this before selecting the material, but it is often over-looked. If you take a look at the diagram above, you will see the wide spectrum of different materials and their properties.

With Sam's and Will's help, we managed to access the machine needed to measure the stiffness and strength of the material. I was told that strength cannot actually be measured until the material breaks, so that is a bit complex. At the graph below, you will see that "stiffness" is actually a function of rise over fall, so a very stiff material will have a high gradient, while a not so stiff material will have a lower gradient. The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (for example, stretching or compression of a rod), the stiffness is defined as k=\frac {F} {\delta} where, F is the force applied on the body δ is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) In the International System of Units, stiffness is typically measured in newtons per metre. In Imperial units, stiffness is typically measured in pounds(lbs) per inch. Uniaxial stress is expressed by \sigma=\frac{F}{A}, where F is the force [N] acting on an area A [m2].[3] The area can be the undeformed area or the deformed area, depending on whether engineering stress or true stress is of interest.

This is the cool machine we used to measure the strength. Sam and Will took us through the steps of attaching the materials between the two rotating knobs and securing them. After that, simply press "start" on the software, and the machine will start to drag the two ends of the respective materials to determine the various properties of the materials.

For this week, I selected three materials: paper, aluminum, and fiberglass composite. The reason I chose these three materials was because I wanted to test the extremes of different materials, as clearly paper has a set of very different properties from aluminum, as from fiberglass composite. This was an interesting material, and I was able to produce pretty distinct results which I will share below.
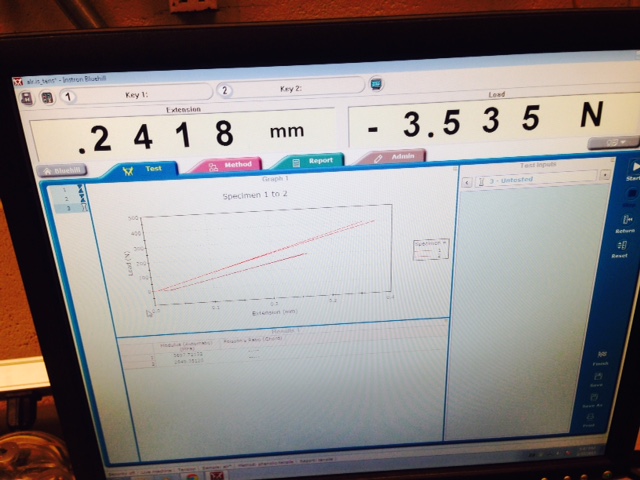
This is the result for the aluminum material.Using the equation of k = F/Change: Stiffness for fiberglass composite = -3.5/0.2418 = -14.47. As you can see from the picture, the composite extended by 0.24818mm. Comparing this to the results for paper which extended by 0.466mm, and aluminum which extended by 0.13mm, it is apparent that aluminum is the most "stiff" of the group, whereas paper is the least stiff, with the fiberglass composite being in the middle.

Here is a paper of the paper being attached between the two knobs and being stretched. I was told that unless the material attached "snaps" or breaks into two, it would not be possible to measure the strength of the material. However, from the results of the load" segment from the three materials, they are as follows, paper: -3.5N, aluminum: 402.9N, fiberglass composite: 377.1N. Using this simple comparison, we can conclude that aluminum has the highest strength as it was able to support 402.9/10 = 40.29kg of weight, while fiberglass was able to support nearly no weight, and paper could hold up to 37kg of weigh. This is an interesting observation as being stiffer does not directly result in a proportional amount of strength, as we can see that aluminum is much stiffer than paper but can support only nearly the same weight as paper!
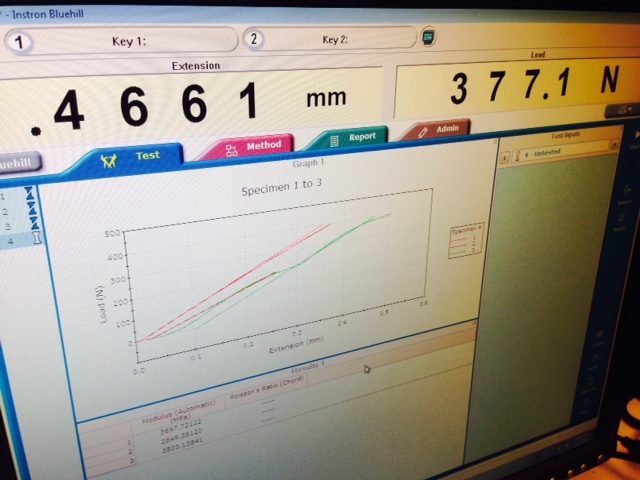
This is the result for the paper material. Using the equation of k = F/Change: Stiffness for paper = 377.1/0.4661 = 809.05