Measurement

For my plotbot I've decided to build a magnetic rotary encoder that can sense a precise angle.

The idea: use 4 hall sensors to magically calculate the exact orientation of the wheel. I was assisted by a sensormag article : "Understanding Integrated Hall Effect Rotary Encoders"

Magnetized Wheel

I started by creating a wheel that has a diametric polarity (one direction is positive and the other is negative).

Circuitry

The 4 hall sensors are positioned in the exact distance from the center, offset by 90 degrees from each other.

Test code

The following code loops over 200 steps which equal 360 degrees. after each step It takes a measurement from all the hall sensors. The output is a simple CSV.

void loop() {

  if (Serial.available()>0) {
    Serial.read();
    on = !on;
    a = 0;
  }

  if (on && a<200) {
    Serial.print(a++);
    Serial.print(",");
    Serial.print(analogRead(A0));
    Serial.print(",");
    Serial.print(analogRead(A1));
    Serial.print(",");
    Serial.print(analogRead(A2));
    Serial.print(",");
    Serial.print(analogRead(A3));
    Serial.print("\n");
    digitalWrite(stp, HIGH);   
    delay(10);               
    digitalWrite(stp, LOW);  
    delay(10);
  } else {
    delay(20);
  } 
}

Run

And on the serial monitor:

step, A0, A1, A2, A3
0,513,524,528,510
1,511,526,526,511
2,511,527,526,509
3,513,525,528,508
....
....
197,512,524,526,511
198,511,525,526,512
199,513,524,528,509

Math

I imported the above csv into google sheets, replaced steps with angle (steps*1.8) and plotted the table.

I performed basic calibration by offsetting each value to by it's neutral value and normalizing the values between min and max amplitude.

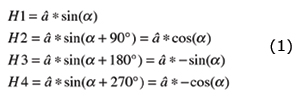
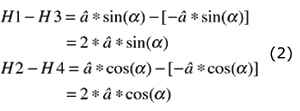
Given that we know how all these functions behave I could now calculate all the angles (with an offset because I didn't start from an angle of 0)

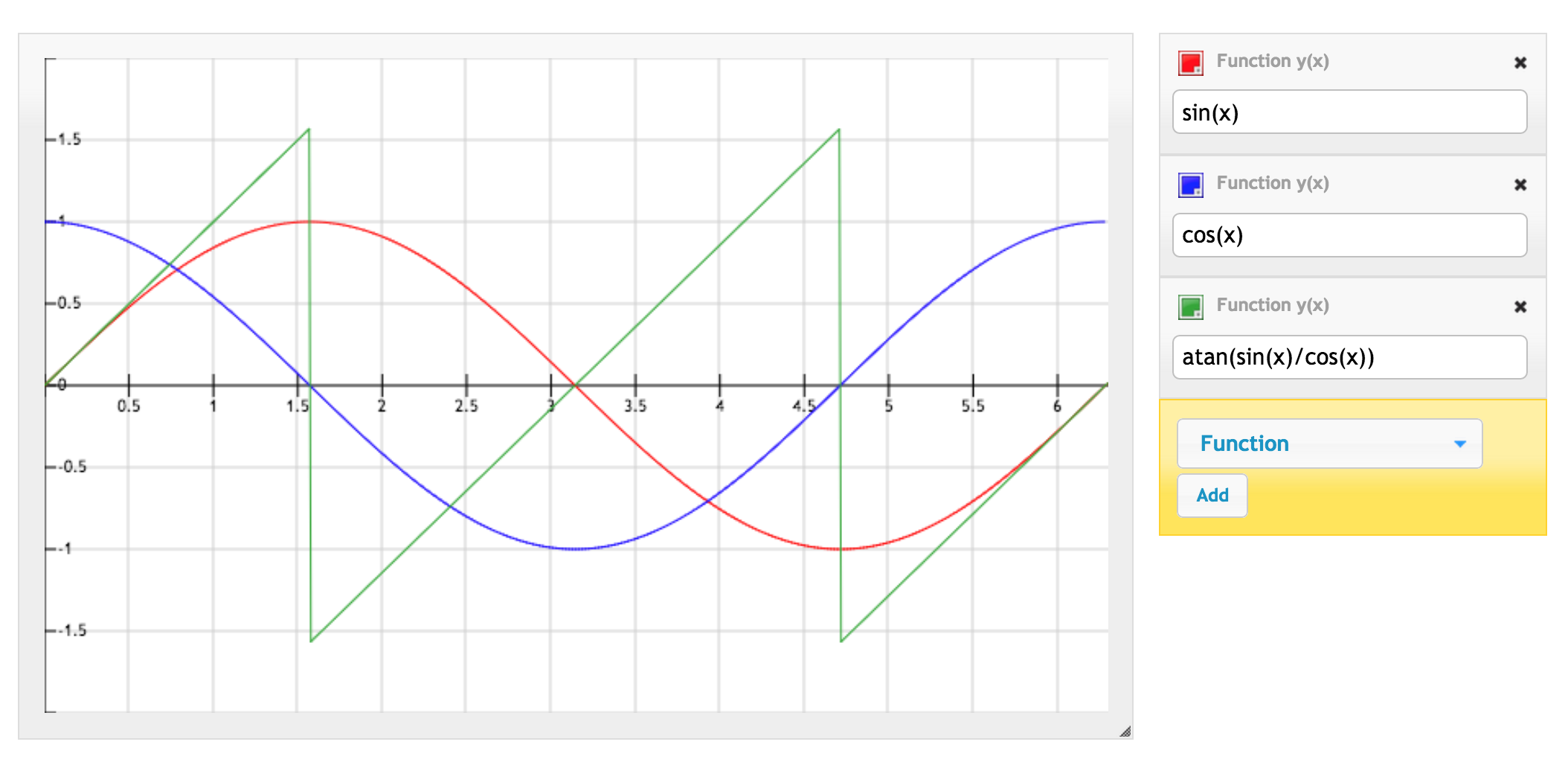
Comparing my calculated angle steps to the original angle steps show a variance of 4.702 degrees and a standard deviation of 2.168 degrees.

This is not good enough, I then tried to improve this by using more precise analog reads. This is possible with an arduino uno using oversampling. This is a very wasteful procedure so I'll only use it for testing.

Using an analog oversampling library I recreated the experiment with 14 bit precision and averaged 3 measurements per step.

Going through the entire process again I achieve a variance of 0.130 degrees and standard deviation of 0.361 degrees. Not so bad!