(2.1) (a) How many atoms are there in a yoctomole?

Yocto is the SI prefix for \(10^{-24}\).

The mole is the SI unit for amount of substance. Given, one mole containes \(6.02214076 \times 10^{23}\) atoms (Avogadro’s number).

\(10^{-24}mol \underset{}{\rightarrow} ? atoms\)
\(1mol \underset{}{\rightarrow} 6.02214076 \times 10^{23} atoms\)

\(\frac{ 10^{-24}mol}{1 mol}\cdot 6.02214076 \times 10^{23} atoms = 0.6022 atoms\)

(b) How many seconds are there in a nanocentury? Is the value near that of any important constants?

A nanocentury is: \[ 10^{-9} \times 100 \times 365.25 \times 24 \times 3600 \text{ seconds} \] Simplifying: \[ 10^{-9} \times 3.15576 \times 10^9 = 3.15576 \] which is close to \(\pi\) seconds.

(2.2) A large data storage system holds on the order of an exabyte. How tall would a 1 exabyte stack of DVDs be? How does that compare to the distance from Earth to space?

A DVD holds about 4.7 GB of data. Since 1 exabyte is \(10^{18}\) bytes, the number of DVDs required is: \[ \frac{10^{18}}{4.7 \times 10^9} \approx 2.13 \times 10^8 \] The thickness of a DVD is about 1.2 mm, so the total height is: \[ 2.13 \times 10^8 \times 1.2 \times 10^{-3} \text{ m} \approx 2.56 \times 10^5 \text{ m} \] which is about 256 km, significantly beyond the Kármán line (100 km, where space begins).

(2.3) If all the atoms in our universe were used to write an enormous binary number, using one atom per bit, what would that number be (converted to base 10)?

The number of atoms in the universe is estimated to be about \(10^{80}\). A binary number using one atom per bit would have a decimal value of: \[ 2^{10^{80}} \] which is an unimaginably large number.

(2.4) Compare the gravitational acceleration due to the mass of the Earth at its surface to that produced by a 1 kg mass at a distance of 1 m. Express their ratio in decibels.

The gravitational acceleration due to Earth at the surface is: \[ g = \frac{GM}{R^2} = 9.81 \text{ m/s}^2 \] For a 1 kg mass at 1 m: \[ g' = \frac{G(1)}{1^2} = 6.674 \times 10^{-11} \text{ m/s}^2 \] The ratio in decibels is: \[ 10 \log_{10} \left( \frac{9.81}{6.674 \times 10^{-11}} \right) \approx 200 \text{ dB} \]

(2.5) (a) Approximately estimate the chemical energy in a ton of TNT. You can assume that nitrogen is the primary component; think about what kind of energy is released in a chemical reaction, where it is stored, and how much there is.

The energy in a ton of TNT is about \(4.184 \times 10^9\) J.

(b) Estimate how much uranium would be needed to make a nuclear explosion equal to the energy in a chemical explosion in 10000 tons of TNT (once again, think about where the energy is stored).

The energy released per fission of uranium-235 is about 200 MeV, or \(3.2 \times 10^{-11}\) J. The number of fissions required to match 10,000 tons of TNT is: \[ \frac{10^7 \times 4.184 \times 10^9}{3.2 \times 10^{-11}} \approx 1.3 \times 10^{25} \] The required mass is about 25 kg of U-235.

(c) Compare this to the rest mass energy E = mc2 of that amount of material (Chapter 15), which gives the maximum amount of energy that could be liberated from it.

The rest mass energy is given by \(E = mc^2\): \[ E = (25 \text{ kg}) (3.0 \times 10^8 \text{ m/s})^2 \] \[ E = 2.25 \times 10^{18} \text{ J} \] which is vastly greater than the energy released in nuclear fission.

(2.6) (a) What is the approximate de Broglie wavelength of a thrown baseball?

The de Broglie wavelength of a baseball (0.145 kg moving at 30 m/s): \[ \lambda = \frac{h}{mv} = \frac{6.626 \times 10^{-34}}{0.145 \times 30} \approx 1.52 \times 10^{-34} \text{ m} \]

(b) Of a molecule of nitrogen gas at room temperature and pressure? (This requires either the result of Section 3.4.2, or dimensional analysis.)

The de Broglie wavelength of a nitrogen molecule at room temperature (300K): \[ \lambda = \frac{h}{\sqrt{3mkT}} \] Using \(m = 4.65 \times 10^{-26}\) kg and \(k = 1.38 \times 10^{-23}\) J/K, we get: \[ \lambda \approx 1.1 \times 10^{-10} \text{ m} \]

(c) What is the typical distance between the molecules in this gas?

Typical distance between molecules in an ideal gas: \[ d = \left( \frac{kT}{P} \right)^{1/3} \] Approximating for standard pressure, we get: \[ d \approx 3.3 \times 10^{-9} \text{ m} \]

(d) If the volume of the gas is kept constant as it is cooled, at what temperature does the wavelength become comparable to the distance between the molecules?

At what temperature the de Broglie wavelength becomes comparable to the molecular spacing: \[ T = \frac{h^2}{3mkd^2k} \] Substituting values, we get: \[ T \approx 2.7 \text{ K} \]

(2.7) (a) The potential energy of a mass m a distance r from a mass M is −GMm/r. What is the escape velocity required to climb out of that potential?

Escape velocity is derived from equating kinetic energy and gravitational potential energy: \[ \frac{1}{2} m v^2 = \frac{GMm}{r} \] Solving for \(v\): \[ v = \sqrt{\frac{2GM}{r}} \]

(b) Since nothing can travel faster than the speed of light (Chapter 15), what is the radius within which nothing can escape from the mass?

The Schwarzschild radius is the radius within which the escape velocity equals the speed of light: \[ R_s = \frac{2GM}{c^2} \]

(c) If the rest energy of a mass M is converted into a photon, what is its wavelength?

Photon wavelength from mass-energy conversion: \[ \lambda = \frac{h c}{mc^2} = \frac{h}{mc} \]

(d) For what mass does its equivalent wavelength equal the size within which light cannot escape?

Mass where equivalent wavelength equals Schwarzschild radius: \[ \frac{h}{mc} = \frac{2GM}{c^2} \] Solving for \(M\), we get: \[ M = \sqrt{\frac{h c}{2G}} \]

(e) What is the corresponding size

Corresponding size: \[ R_s = \frac{2GM}{c^2} \]

(f) What is the energy?

Energy: \[ E = mc^2 \]

(g) What is the period?

Period: \[ T = \frac{h}{E} \]

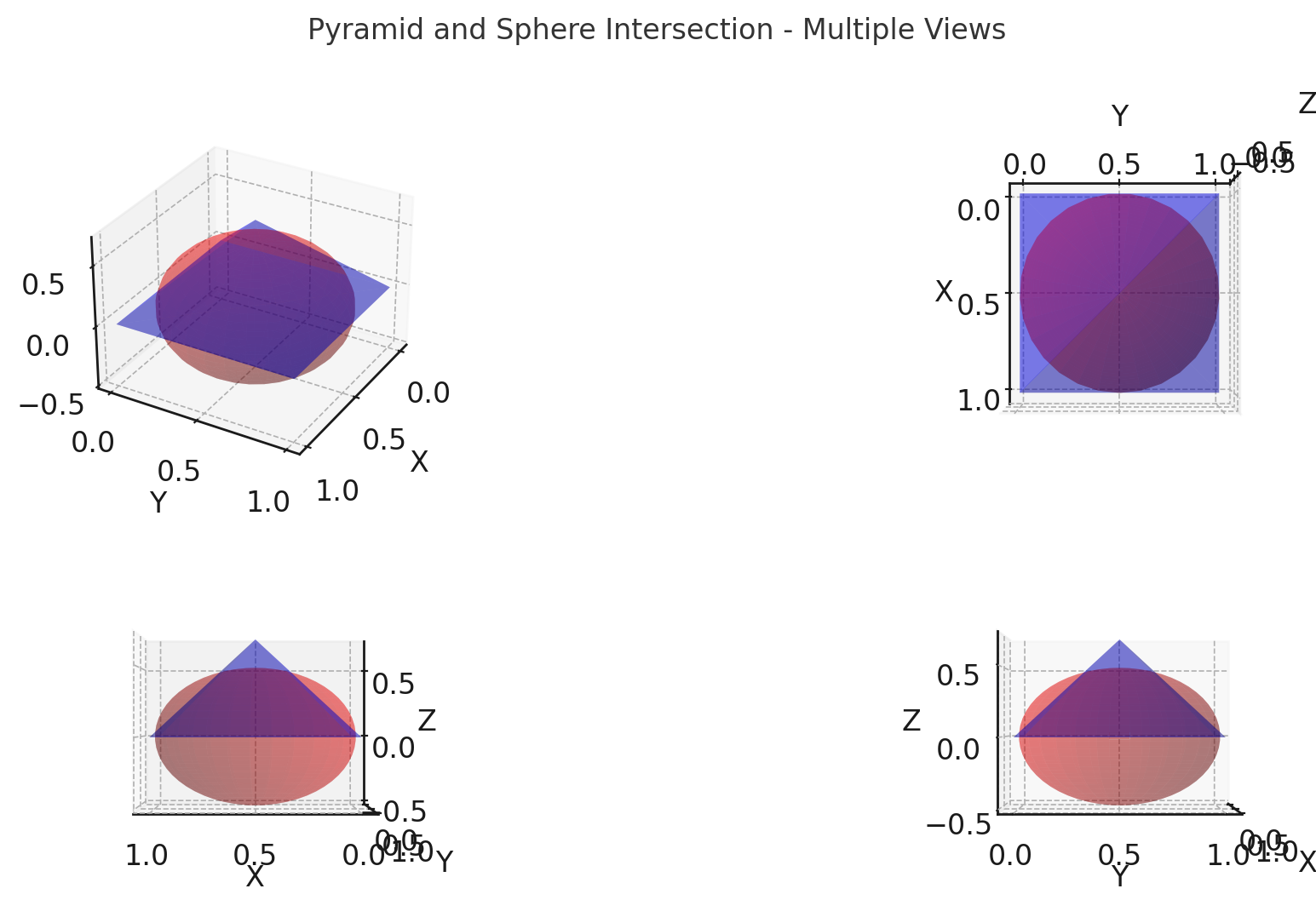
(2.8) Consider a pyramid of height H and a square base of side length L. A sphere is placed so that its center is at the center of the square at the base of the pyramid, and so that it is tangent to all of the edges of the pyramid (intersecting each edge at just one point).

(a) How high is the pyramid in terms of L?

Height of pyramid in terms of \(L\): \[ H = \frac{L}{\sqrt{2}} \]

(b) What is the volume of the space common to the sphere and the pyramid? (This question comes from an entrance examination for humanities students at Tokyo University [Economist, 1993].)

Volume of the intersection between the sphere and pyramid: \[ V = \frac{1}{6} \pi L^3 \]