Quantization of Flux around a Superconducting Loop¶
$$\newcommand{\ket}[1]{\left|{#1}\right\rangle}$$$$\newcommand{\bra}[1]{\left\langle{#1}\right|}$$Superconductors exhibit long range phase coherence because it's energetically favorable for overlapping cooper pairs to be coherent. Therefore, the wavefunction of a superconductor can be approximated as an ensemble average wavefunction
$$ \psi(\vec r) = |\psi(\vec r)|e^{i\theta(\vec r)} $$where $\theta(\vec r)$ is a scalar function of the phase of the electron pairs and $\psi(\vec r)$ is typically normalized so that $\psi^*\psi = n_c(\vec r) $ where $n_c(\vec r)$ is the effective density of cooper pairs and can usually be taken to be spatially constant.
The momentum for a single cooper in a weak magnetic field is $$\vec p = m^*\vec v_s + e^*\vec A$$ where $m^* = 2m_e$ and $e^* = 2e$ are the effectie mass and charge of the pair. Extrapolating to all pairs $$ n_c\vec p = n_c (m^*\vec v_s + e^*\vec A) = \bra{\psi}-i\hbar\nabla\ket{\psi}$$ \ $$\bra{\psi}-i\hbar\nabla\ket{\psi} \\ = \bra{\psi}-i\hbar\sqrt{n^*}e^{i\theta(\vec r)} \cdot i\nabla\theta \\ = \bra{\psi}\hbar\nabla\theta\psi \\ = \hbar\nabla\theta\psi^*\psi \\ = n_c\hbar\nabla\theta $$ \ $$ n_c\vec p = n_c\hbar\nabla\theta \\ \vec p = \hbar\nabla\theta = m^*\vec v_s + e^*\vec A $$ and in terms of the superconducting current density and London's penetration depth $$ \vec p = \hbar\nabla\theta = e^*(\Lambda\vec J_s + \vec A) \\ \Lambda = \frac{m^*}{n_ce^{*2}} $$
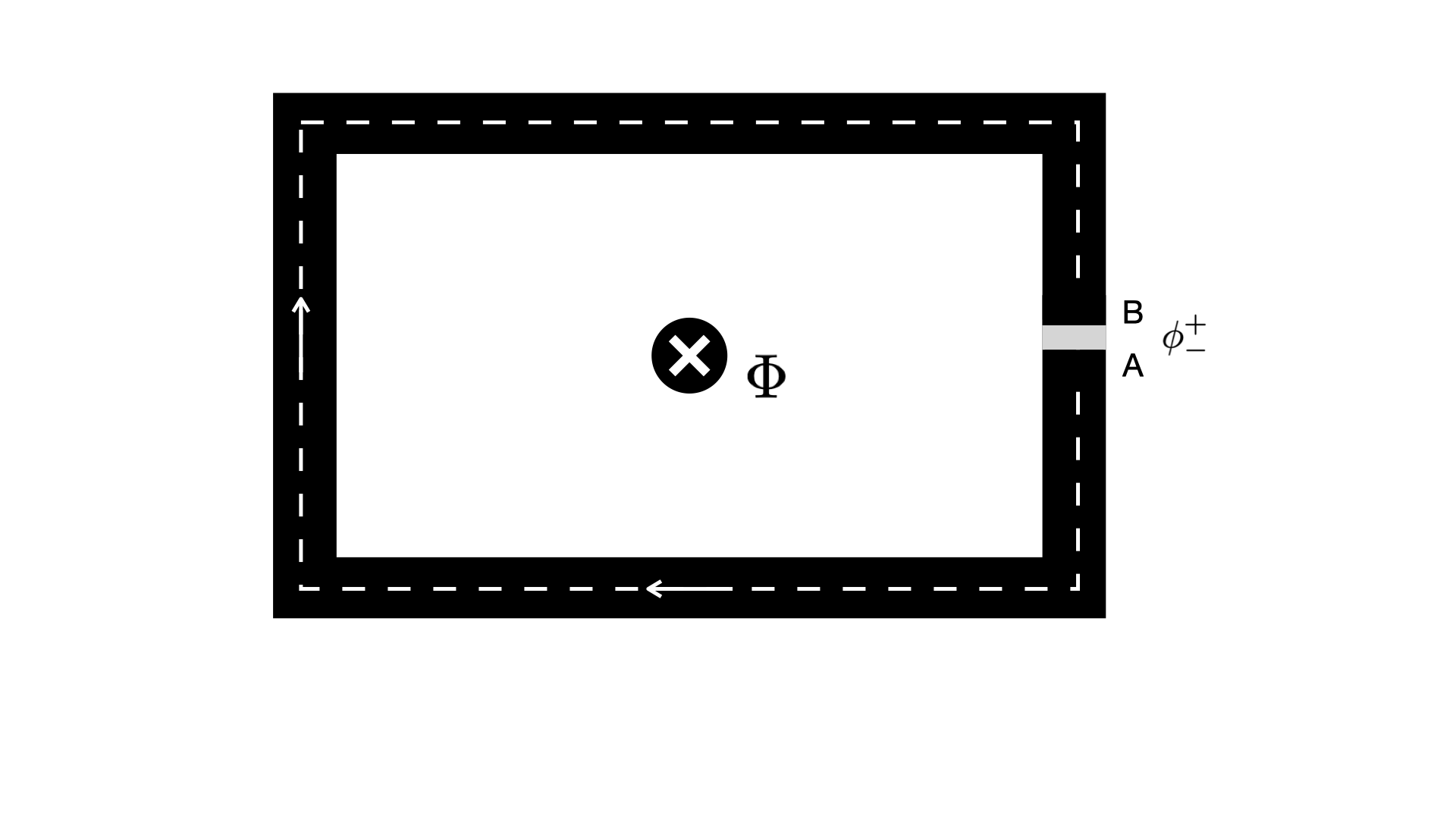
For a supercondcutor with a hole of non-superconducting material, shown in the image below.

The momentum around the contour C must be $$ \oint\vec p \cdot d\vec l = \hbar\oint\nabla\theta\cdot d\vec l = e_c\oint(\Lambda \vec J_s + \vec A)\cdot d\vec l $$ The closed loop integral across the phase change must be a multiple of $2\pi$ and we'll assume that the contour is deep enough into the material so the current is 0. Then the equation simplies to $$ \hbar 2n\pi = e^*\oint\vec A\cdot d\vec l \\ \hbar 2n\pi = e^*\int_s (\nabla \times\vec A) dS \\ \hbar 2n\pi = e^*\int_s \vec B \cdot d\vec S \\ \hbar 2n\pi = e^* \Phi_s $$ Using Stoke's theorem in the definition of magnetic field, we get an equation for the flux through the non-superconducting loop which is quantized. $$ \Phi_s = \frac{hn}{2e} = n\Phi_0 \qquad n = 0, 1, 2, . . . $$ and $\Phi_0$ is the basic quantum of magnetic flux described by fundamental constants $$ \Phi_0 = \frac{h}{2e} = 2.07\times 10^{-15} \text{Wb} $$