# Copyright 2022 Jorgen Bergstrom
# See also code from http://compmech.lab.asu.edu/codes.php
# Additions by Nicole Bakker (in the comments)
import numpy as np
import math
from matplotlib import pyplot as plt
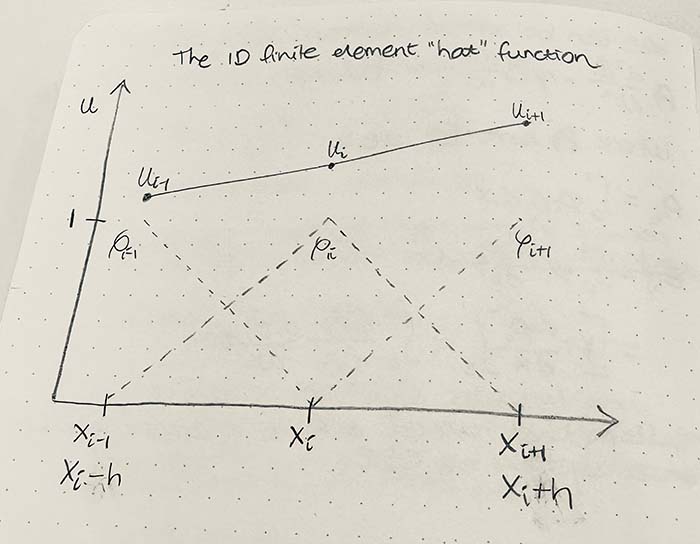
def shape(xi):
x,y = tuple(xi)
N = [(1.0-x)*(1.0-y), (1.0+x)*(1.0-y), (1.0+x)*(1.0+y), (1.0-x)*(1.0+y)]
return 0.25*np.array(N)
def gradshape(xi):
x,y = tuple(xi)
dN = [[-(1.0-y), (1.0-y), (1.0+y), -(1.0+y)],
[-(1.0-x), -(1.0+x), (1.0+x), (1.0-x)]]
return 0.25*np.array(dN)
fig = plt.figure() # Adding this for labels
ax = fig.add_subplot(111) # Adding this for labels
print('create mesh')
# input
mesh_ex = 9
mesh_ey = 49
mesh_lx = 10.0
mesh_ly = 50.0
# derived
mesh_nx = mesh_ex + 1
mesh_ny = mesh_ey + 1
num_nodes = mesh_nx * mesh_ny
num_elements = mesh_ex * mesh_ey
mesh_hx = mesh_lx / mesh_ex
mesh_hy = mesh_ly / mesh_ey
nodes = []
for y in np.linspace(0.0, mesh_ly, mesh_ny):
for x in np.linspace(0.0, mesh_lx, mesh_nx):
nodes.append([x,y])
nodes = np.array(nodes)
conn = []
for j in range(mesh_ey):
for i in range(mesh_ex):
n0 = i + j*mesh_nx
conn.append([n0, n0 + 1, n0 + 1 + mesh_nx, n0 + mesh_nx])
print ('material model - plane strain')
E = 100.0
v = 0.48
C = E/(1.0+v)/(1.0-2.0*v) * np.array([[1.0-v, v, 0.0],
[ v, 1.0-v, 0.0],
[ 0.0, 0.0, 0.5-v]])
print('create global stiffness matrix')
K = np.zeros((2*num_nodes, 2*num_nodes))
q4 = [[x/math.sqrt(3.0),y/math.sqrt(3.0)] for y in [-1.0,1.0] for x in [-1.0,1.0]]
B = np.zeros((3,8))
for c in conn:
xIe = nodes[c,:]
Ke = np.zeros((8,8))
for q in q4:
dN = gradshape(q)
J = np.dot(dN, xIe).T
dN = np.dot(np.linalg.inv(J), dN)
B[0,0::2] = dN[0,:]
B[1,1::2] = dN[1,:]
B[2,0::2] = dN[1,:]
B[2,1::2] = dN[0,:]
Ke += np.dot(np.dot(B.T,C),B) * np.linalg.det(J)
for i,I in enumerate(c):
for j,J in enumerate(c):
K[2*I,2*J] += Ke[2*i,2*j]
K[2*I+1,2*J] += Ke[2*i+1,2*j]
K[2*I+1,2*J+1] += Ke[2*i+1,2*j+1]
K[2*I,2*J+1] += Ke[2*i,2*j+1]
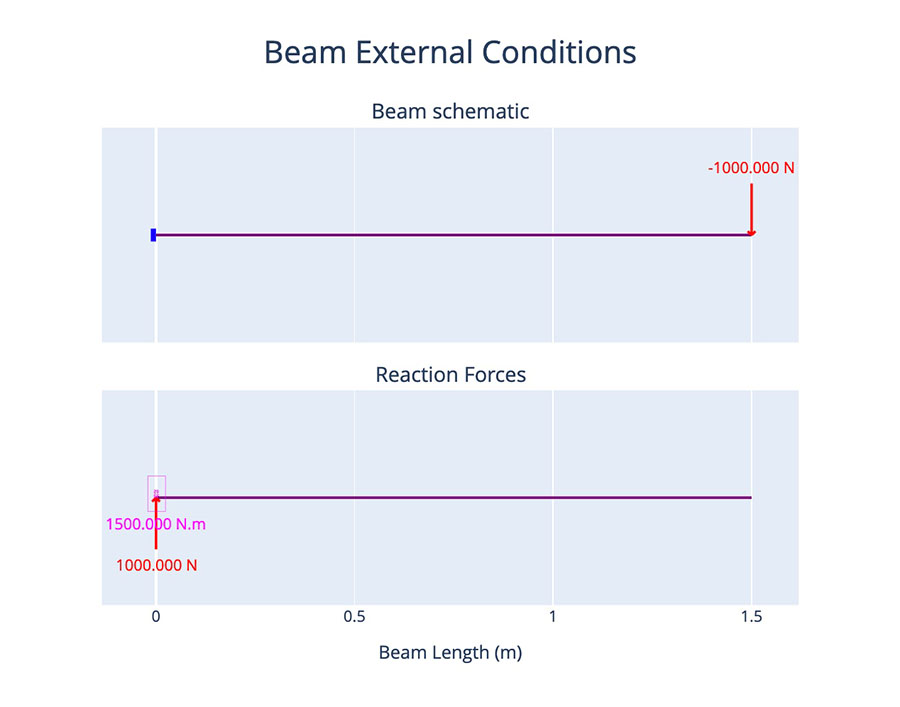
print('assign nodal forces and boundary conditions')
f = np.zeros((2*num_nodes))
for i in range(num_nodes):
if nodes[i,1] == 0.0:
K[2*i,:] = 0.0
K[2*i+1,:] = 0.0
K[2*i,2*i] = 1.0
K[2*i+1,2*i+1] = 1.0
if nodes[i,1] == mesh_ly:
x = nodes[i,0]
f[2*i+1] = 20.0
if x == 0.0 or x == mesh_lx:
f[2*i+1] *= 0.5
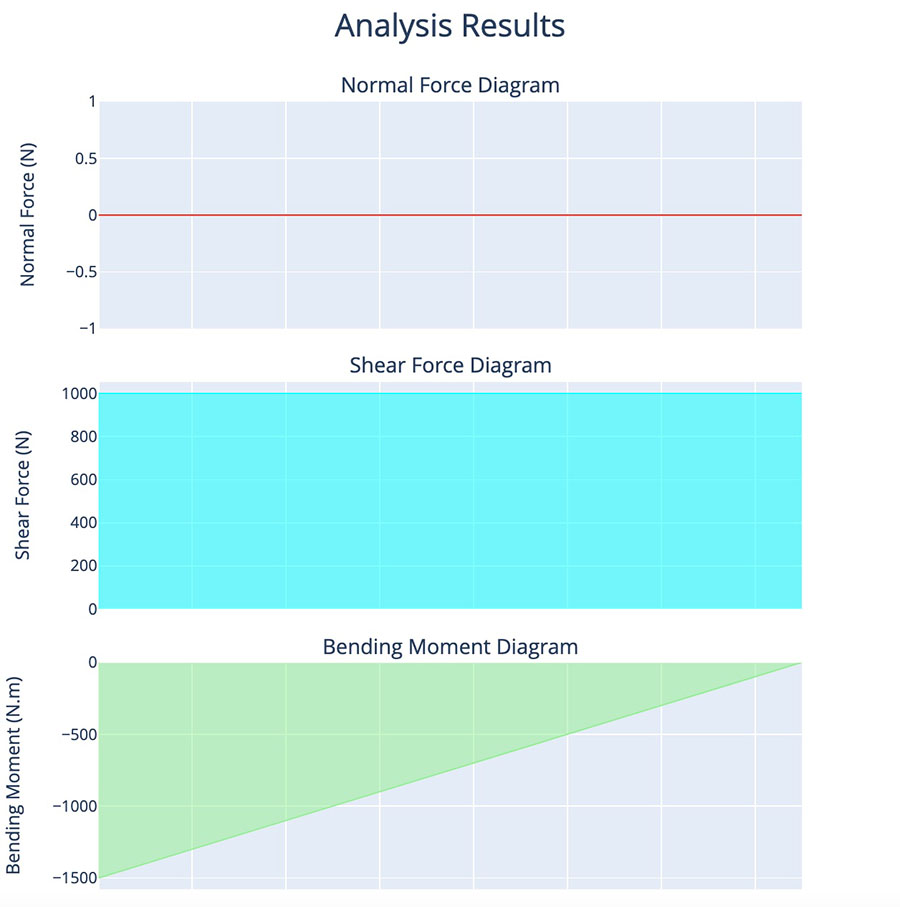
print('solving linear system')
u = np.linalg.solve(K, f)
print('max u=', max(u), 'mm') # Adding units in mm
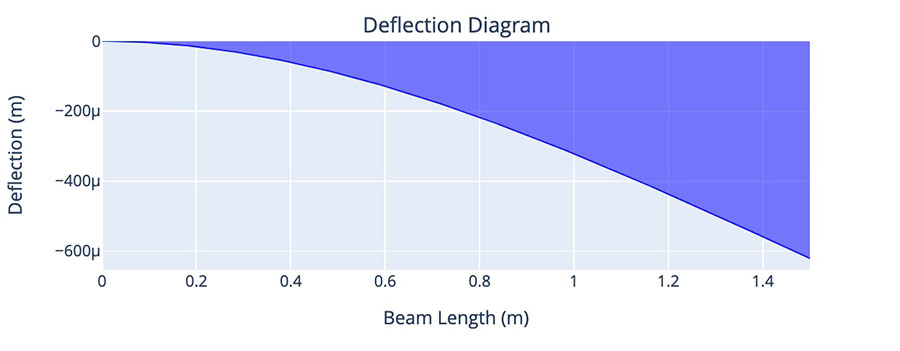
print('plotting displacement')
ux = np.reshape(u[0::2], (mesh_ny,mesh_nx))
uy = np.reshape(u[1::2], (mesh_ny,mesh_nx))
xvec = []
yvec = []
res = []
for i in range(mesh_nx):
for j in range(mesh_ny):
xvec.append(i*mesh_hx + ux[j,i])
yvec.append(j*mesh_hy + uy[j,i])
res.append(uy[j,i])
t = plt.tricontourf(xvec, yvec, res, levels=14, cmap=plt.cm.jet)
plt.scatter(xvec, yvec, marker='o', c='b', s=2)
plt.suptitle('FEA beam', fontsize = 12) # Added a title
ax.set_xlabel('x') # Added x label
ax.set_ylabel('y') # Added y label
plt.grid()
plt.colorbar(t, label="Displacement u",) # Added a label
plt.axis('equal')
plt.show()