information in physical systems

4.1

Verify that the entropy function satisfies the properties of

1) Continuity Entropy of the information is defined as $H(x) = \sum_{i=1}^{n}p_ilog(p_i)$ where $p_i$ is a probability measure which means it can be a number between 0 to 1. and log is a continuous function. So H(x) is a continuous function

import matplotlib.pyplot as plt
import numpy as np
#for a coin toss. Probability of tossing head or tail is p and 1-p 
head_probability = np.linspace(0,1,11)
entropy_of_information = -head_probability*np.log(head_probability)-(1-head_probability)*np.log(1-head_probability)
plt.plot(head_probability,entropy_of_information)
plt.xlabel("probability p in a coin toss")
plt.ylabel("entropy")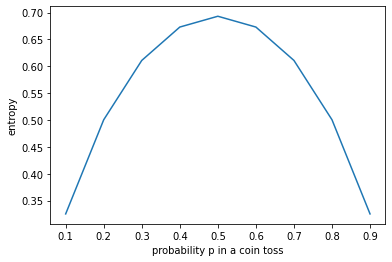

4) independence

For $H(x,y) = - \sum_{x}\sum_{y}p(x,y)log(p(x,y))$ applying baye’s rule $H(x,y) = \sum_{x}\sum_{y}(x)p(y)log(p(x)p(y))$ because of the independence. Therefore, $-\sum_{x}\sum_{y}p(x)p(y)log(p(x)) -\sum_{x}\sum_{y}p(x)p(y)log(p(y)) = -\sum_{x}p(x)log(p(x))-\sum_{y}p(y)log(p(y)) = H(x)+h(y)$

4.2

4.3

Binary channel with a small probability of making an error $\epsilon$

(a) Majority voting is when you send a bit repeatedly - so to send a 1 you send 11111 for n times and then pick the majority one received by the output of the channel y

if you send a bit three times 000 - 0 001 - 0 010-0 100-0 by majority voting 011-1 etc for majority voting when the decoded bit is 1 , If we send a 0 three times, the error of the decoded bit will happen either when 2 of the bits are 1 or all three 1 for other cases, majority voting with ensure that the bit is a 0. similarly for 1. so the probability of error is $3(1-\epsilon)(\epsilon)^2 +\epsilon^3$

(b) voting on top of majority of voting

so we send 0 three times - 011 110 101 111 all are error cases for reading 0 as 1 by majority voting. so we can repeat the same step earlier but now the error probability is $\epsilon_1 = 3(1-\epsilon)(\epsilon)^2 +\epsilon^3$ if $\epsilon$ is small then $\epsilon_1 = 3\epsilon^2$=$3(\epsilon)^2$. so error now is 27$\epsilon^4$

(c) so if we keep doing this N times this becomes a multiple of the $\epsilon^{2^N}$

4.4

4.5

(a) going back to earlier class, SNR in db is $SNR = 10log_{10}(P_{signal}/P_{noise})$ so 20dB is like 100 of the ration. going back to 4.29, channel capacity = 3300*log_2(1+100)=21971.4 = 21kbits/second

(b) subsitute Gbit/s into 4.29 with 3300 hz and compute SNR in db

$(2^{10^9})/3300 = 1+S/N = S/N$, in dB = 10$log_{10}S/N = 10log_{10}2^{10^{9}}-10log_{10}3300$=$10^{10}*0.301 -35$

4.6

Making an unbiased estimator of $x_0$. Since $(x_1,x_2,...x_n)$ are drawn from a guassian distribution with the variance $\sigma^2$ and means $x_0.$

If $f(x_1,x_2...x_n)$ is an unbiased estimator then the $E[f(x_1,x_2...x_n)] = E[\frac{1}{n}\sum_{i=1}^{n}x_i] = \frac{1}{n}\sum_{i=1}^{n}E[x_i] = \frac{1}{n}*nx_0 = x_0$

Therefore $f(x_1,x_2,...x_n)$ is an unbiased estimator of $x_0$

Cramer-Rao lower bound gives information about the minimum variance of the unbiased estimator - which in our case is f(x_1,x_2...x_n) = $x_0 = \frac{1}{n}\sum_{i=1}^{n}x_i$

Fisher information from 4.32 is the variance of the score = $E[<V^2>]$ =$E[(\frac{d}{dx_0}log\frac{1}{2*\pi*\sigma^2}exp^{-\frac{(x-x_0)^2}{2*\sigma^2}})^2]$ = $E[(\frac{d}{dx_0}{-\frac{(x-x_0)^2}{2*\sigma^2}})^2] = E[(\frac{x-x_0}{\sigma^2})^2]$ =$\frac{E[(x-x_0)^2]}{\sigma^4} = \frac{\sigma^2}{\sigma^4} = 1/\sigma^2$

From 4.34 - $n/\sigma^2$

variance of the estimator = E[f^2]-E[f]^2

= $1/n^2(E[(\sum_{i=1}^{n}x_i)^2]-E[\sum_{i=1}^{n}x_i]^2)$ = n/n^2*variance +covariance terms

Link - https://www.notion.so/alienrobotfromthefutures/Final-Project-65ca8d3338ab4ee48e30fa6b5e1fca93