Week 4 - Finite Differences: PDEs

Problem 8.1:

Consider the 1D wave equation $ \frac{\partial^2 u}{\partial t^2} = v^2 \frac{\partial^2 u}{\partial x^2} $

(a) Write down the straightforward finite-difference approximation.

$$ \begin{split} \frac{\partial^2 u}{\partial x^2} = \frac{u^n_{j+1} -2u^n_j + u^n_{j-1}}{\Delta x^2} + O(\Delta x^2) \\ \frac{\partial^2 u}{\partial t^2} = \frac{u^{n+1}_{j} -2u^{n}_{j} + uu^{n-1}_{j}}{\Delta t^2} + O(\Delta t^2) \end{split} $$$$ v^2 \frac{u^{n}_{j+1} -2u^{n}_{j} + u^{n}_{j-1}}{\Delta x^2} + O(\Delta x^2) = \frac{u^{n+1}_{j} -2u^{n}_{j} + u^{n-1}_{j}}{\Delta t^2} + O(\Delta t^2) $$$$ \begin{split} u^{n+1}_{j} &= v^2(\Delta t)^2 \frac{u^{n}_{j+1} -2u^{n}_{j} + u^{n}_{j-1}}{\Delta x^2} + 2u^{n}_{j} - uu^{n-1}_{j} + \Delta t^2 (O(\Delta x^2) + O(\Delta t^2)) \\ &= v^2(\Delta t)^2 \frac{u^{n}_{j+1} -2u^{n}_{j} + u^{n}_{j-1}}{\Delta x^2} + 2u^{n}_{j} - uu^{n-1}_{j} + O(\Delta t^2 \Delta x^2) + O(\Delta t^4)) \end{split} $$

(b) What order approximation is this in time and in space?

(c) Use the von Neumann stability criterion to find the mode amplitudes.

(d) Use this to find a condition on the velocity, time step, and space step for stability.

(e) Do different modes decay at different rates for the stable case?

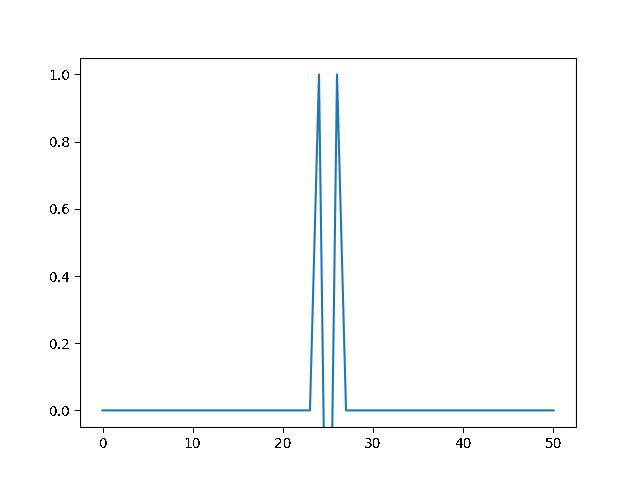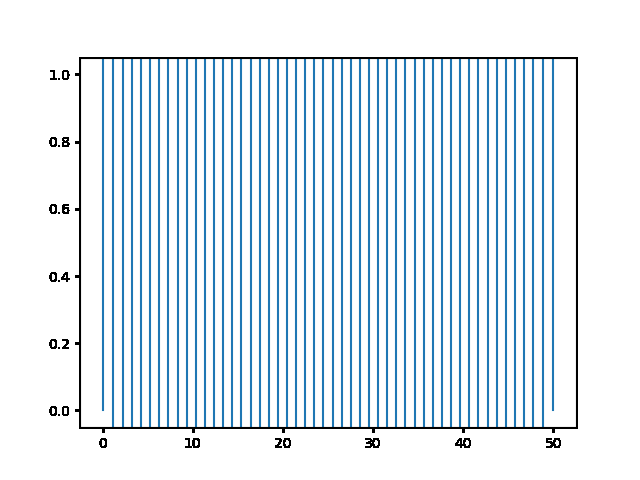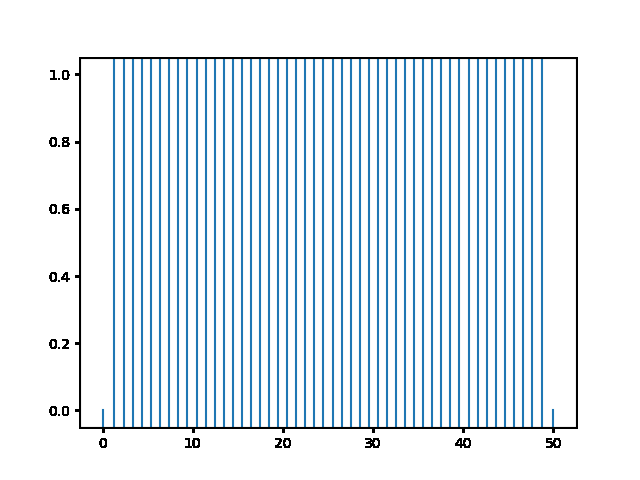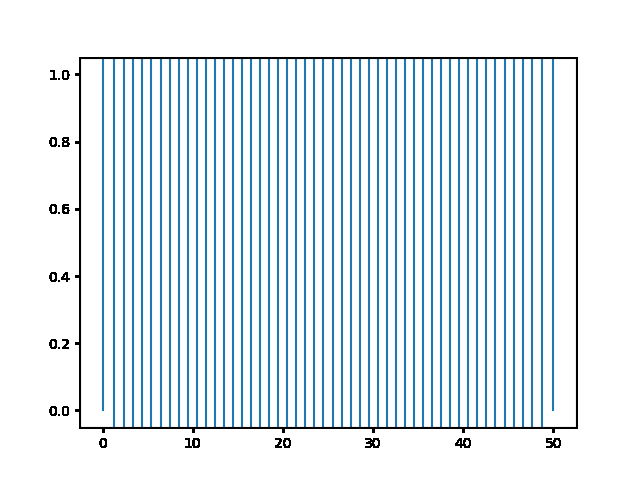
(f) Numerically solve the wave equation for the evolution from an initial condition with $u = 0$ except for one nonzero node, and verify the stability criterion.

In [ ]:

(g) If the equation is replaced by $ \frac{\partial^2 u}{\partial t^2} = v^2 \frac{\partial^2 u}{\partial x^2} + \gamma \frac{\partial}{\partial t} \frac{\partial^2 u}{\partial x^2} $ , assume that $u(x,t) = Ae^{i(kx-\omega t)} $ and find a relationship between $k$ and $\omega$, and simplify it for small $\gamma$. Comment on the relationship to the preceeding question.

(h) Repeat the numerical solution of the wave equation with the same initial conditions, but include the damping term.

In [ ]:

Problem 8.2:

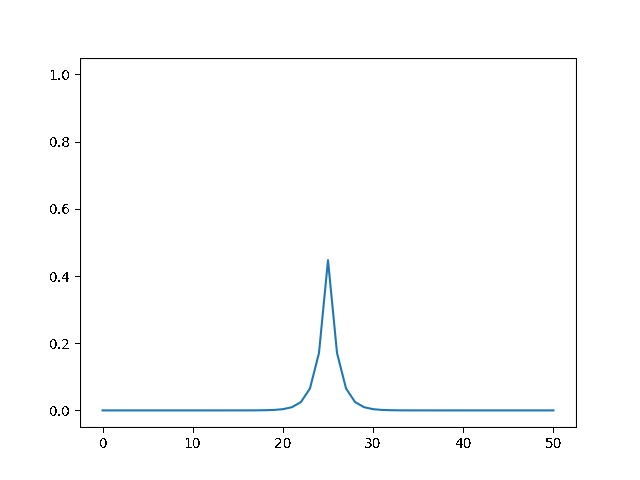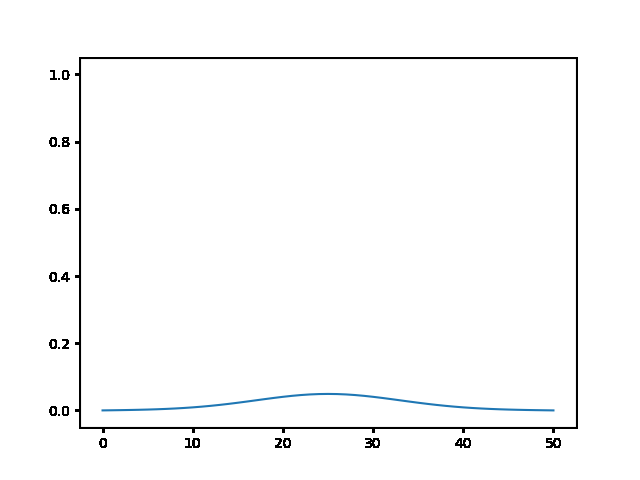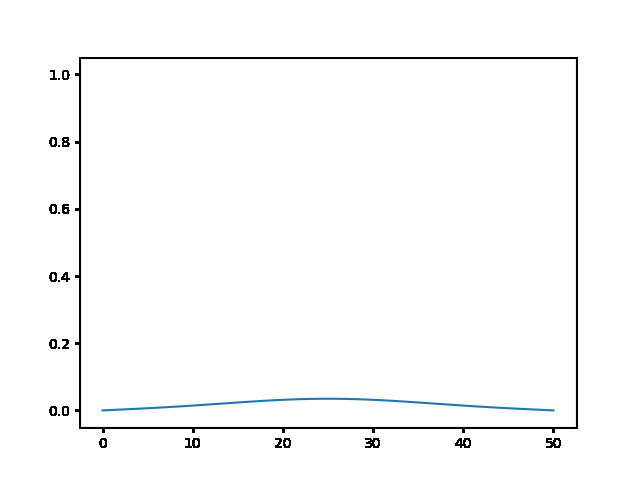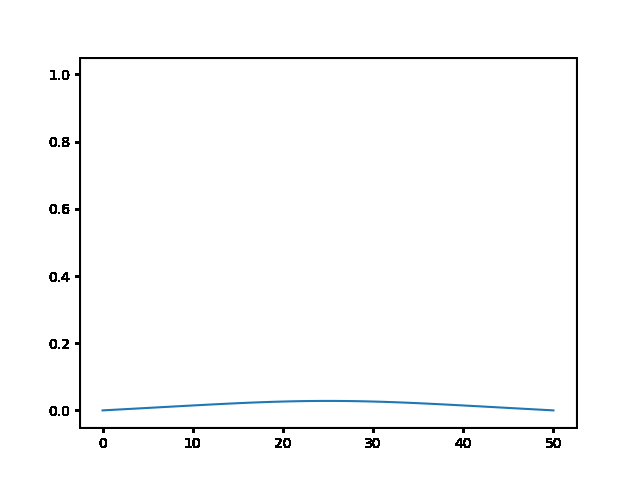
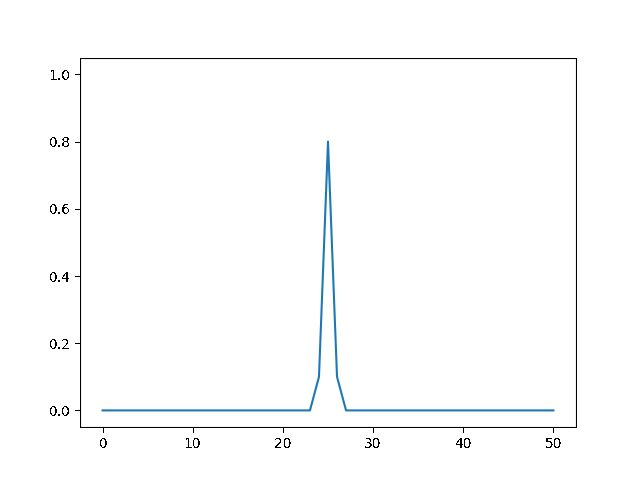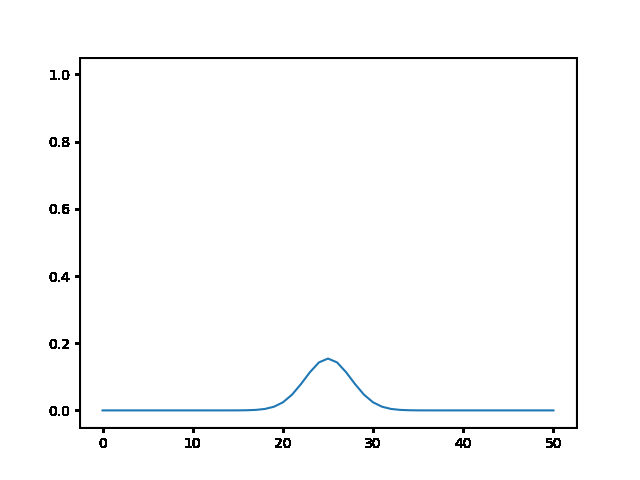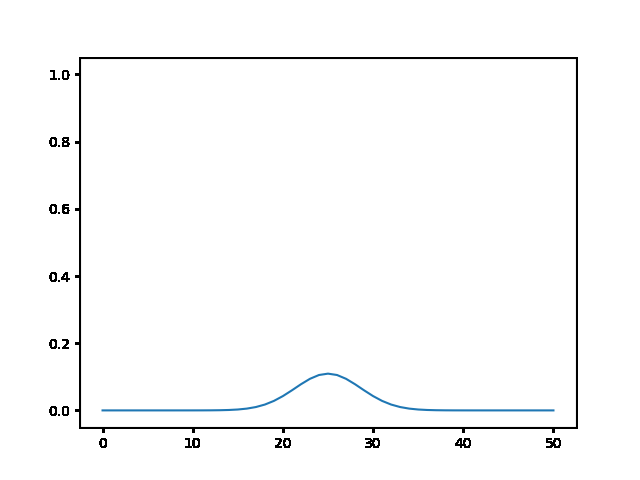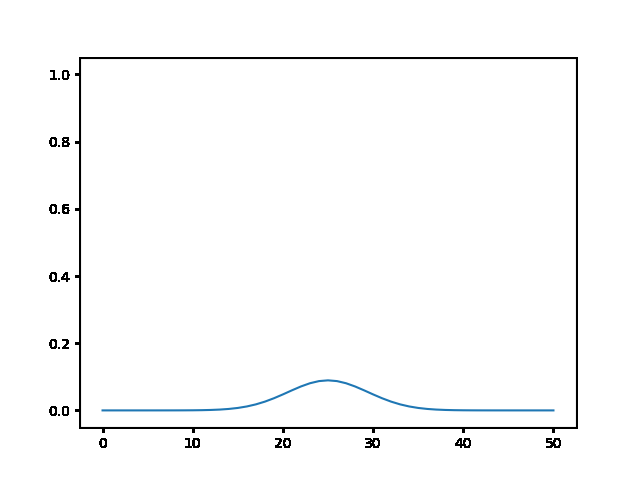
Write a program to solve a $1D$ diffusion problem on a lattice of 500 sites, with an initial condition of zero at all the sites, except the central site which starts at the value 1.0. Take $D = \Delta x = 1$, and use fixed boundary conditions set equal to zero.

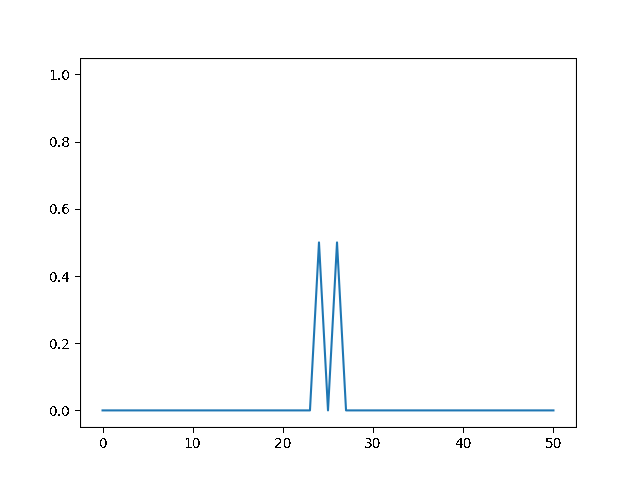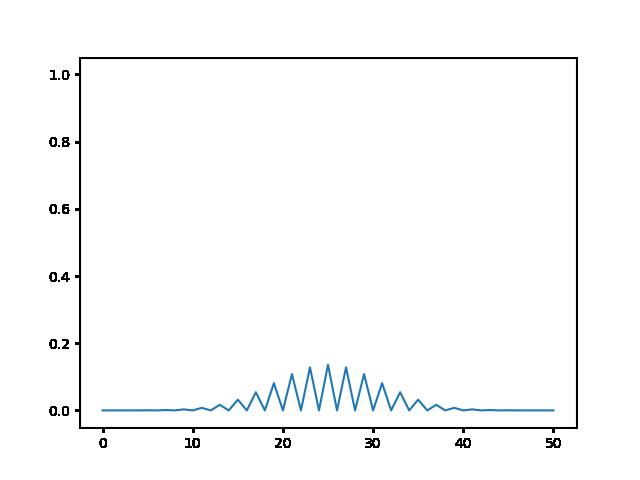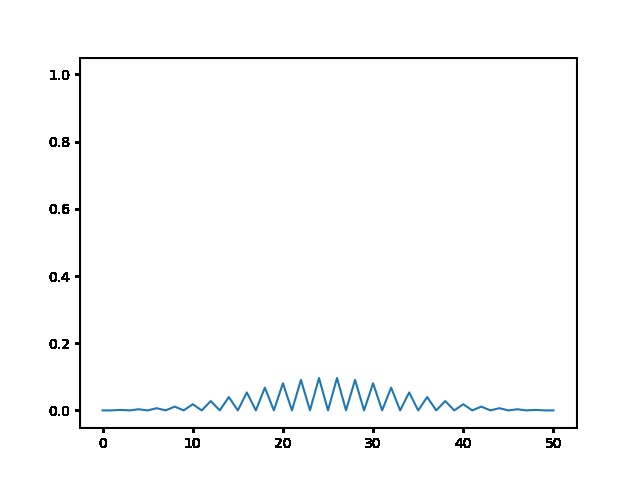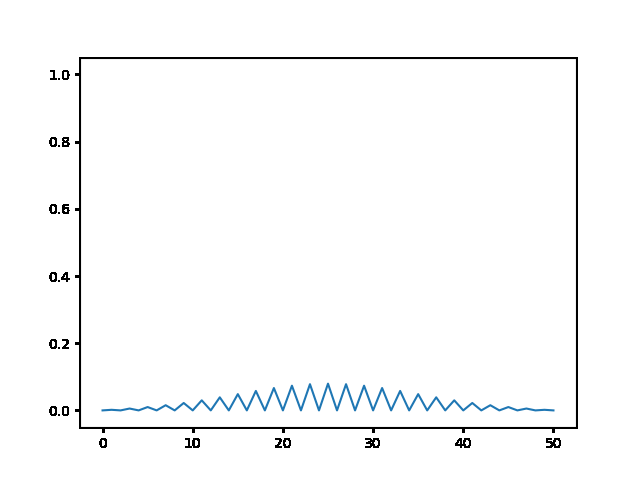
(a) Use the explicit finite difference scheme, and look at the behavior for $\Delta t = 1,0.5,$ and $0.1$. What step size is required by the Courant condition?

The required time step is $ \Delta t \leq 0.5 $. For bigger time step the explicit method explodes, while the implicit one holds!

In [ ]:
%%javascript
    
var kernel = IPython.notebook.kernel;

function explicit_step(D, Dx, Dt, u_old){
    var u_new = []
    for (var i=0; i<u_old.length; i++){u_new[i]=0}

    for (var j = 1; j < u_old.length-1; j++){
        u_new[j] = u_old[j] + (D*Dt/(Dx**2))*(u_old[j+1] -2*u_old[j] + u_old[j-1])
    }
    return u_new
}

function tri_gauss_elimination(A, b){
    // forward pass
    for (var i=1; i<(A.length-1); i++){
        // Assuming no zeros on the diagonal
        A[i][i] -= A[i-1][i]*A[i][i-1]/A[i-1][i-1]
        b[i] -= b[i-1]*A[i][i-1]/A[i-1][i-1]
        A[i][i-1] = 0
    }

    // backward pass
    for (var i=(A.length-2); i>0; i--){
        b[i] -= b[i+1]*A[i][i+1]/A[i+1][i+1]
        A[i][i+1] = 0
    }

    // computation
    var res = []
    for (var i=0; i<b.length; i++){
        res[i] = b[i]/A[i][i]
    }

    return res
}

function implicit_step(D, Dx, Dt, u_old){
    var alpha = D*Dt/(Dx**2)
    var A = []
    for (var i=0; i<u_old.length; i++){
        A.push([])
        for (var j=0; j<u_old.length; j++){A[i][j]=0}
        if (i == 0 || i == u_old.length-1){
            A[i][i] = 1
        } else {
            A[i][i-1] = -alpha
            A[i][i] = 1 + 2*alpha
            A[i][i+1] = -alpha
        }
    }

    var res = tri_gauss_elimination(A, u_old)
    return res
}

var D = 1
var T = 100
var size = 50
var Dx = 1
var Dt = 1

var times = [0]
var u_exp = [[]]
for (var k=0; k<=size; k++){u_exp[0][k]=0}
u_exp[0][size/2] = 1
var u_imp = [[]]
for (var k=0; k<=size; k++){u_imp[0][k]=0}
u_imp[0][size/2] = 1

for (var t=Dt; t<=T; t += Dt){
    u_exp.push(explicit_step(D, Dx, Dt, u_exp[u_exp.length-1].slice()))
    u_imp.push(implicit_step(D, Dx, Dt, u_imp[u_imp.length-1].slice()))
    times.push(t)
}

kernel.execute("u_exp = " + u_exp)
kernel.execute("u_imp = " + u_imp)
kernel.execute("times = " + times)
kernel.execute("lattice_size = " + size)
In [ ]:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animations
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
import time
%matplotlib notebook
In [ ]:
u_exp = np.reshape(np.array(u_exp), (-1, lattice_size+1))

i = 0
fig, ax = plt.subplots()
line, = ax.plot(list(range(lattice_size+1)), u_exp[i])
line.title = 'explicit Delta t = 1'

def updatefig(*args):
    global i
    line.set_ydata(u_exp[i])
    i = (i+1) % len(u_exp)
    return line, 

ani = animations.FuncAnimation(fig, updatefig, np.arange(100), 
                              interval=25, blit=True)
ani.save('gifs/exp1.gif', writer='imagemagick', fps=60)
plt.show()
In [1]:
%%html
explicit, Dt = .1 :
<img src="gifs/exp.1.gif">
explicit, Dt = .5 :
<img src="gifs/exp.5.gif">
explicit, Dt = 1 :
<img src="gifs/exp1.gif">
explicit, Dt = .1 : explicit, Dt = .5 : explicit, Dt = 1 :

(b) Now repeat this using implicit finite differences and compare the stability.

In [ ]:
u_imp = np.reshape(np.array(u_imp), (-1, lattice_size+1))

i = 0
fig, ax = plt.subplots()
line, = ax.plot(list(range(lattice_size+1)), u_imp[i])
line.title = 'implicit Delta t = 1'

def updatefig(*args):
    global i
    line.set_ydata(u_imp[i])
    i = (i+1) % len(u_imp)
    return line, 

ani = animations.FuncAnimation(fig, updatefig, np.arange(100), 
                              interval=25, blit=True)
ani.save('gifs/imp1.gif', writer='imagemagick', fps=60)
In [2]:
%%html
implicit, Dt = 1 :
<img src="gifs/imp1.gif">
implicit, Dt = 1 :

Problem 8.3

Use ADI to solve a $2D$ diffusion problem on a lattice, starting with randomly seeded values.

In [ ]:
%%javascript

function matmul(A, B){
    var C = []
    
    for (var i=0; i<A.length; i++){
        C.push([])
        for (var j=0; j<B[i].length; j++){
            C[i][j] = 0
            for (var k=0; k<B[i].length; k++){
                C[i][j] += A[i][k]*B[k][j]
            }
        }
    }
    
    return C
}

function td_invert(A){
    var I = []
    var B = []
    for (var i=0; i<A.length; i++){
        B[i] = A[i].slice()
        I.push([])
        for (var j=0; j<A[i].length; j++){I[i][j]=0}
        I[i][i] = 1
    }
    
    // forward pass
    for (var i=1; i<B.length; i++){
        for (var j=0; j<i; j++){
            I[i][j] -= I[i-1][j]*B[i][i-1]/B[i-1][i-1]
        }
        B[i][i] -= B[i-1][i]*B[i][i-1]/B[i-1][i-1] 
        B[i][i-1] = 0
    }
    
    // backward pass
    for (var i=B.length-2; i>0; i--){
        for (var j=0; j<I.length; j++){
            I[i][j] -= I[i+1][j]*B[i][i+1]/B[i+1][i+1]
        }
        B[i][i] -= B[i+1][i]*B[i][i+1]/B[i+1][i+1]  
        B[i][i+1] = 0
    }
    
    // normalizing
    for (var i=0; i<B.length; i++){
        for (var j=0; j<I.length; j++){
            I[i][j] /= B[i][i]
        }
        B[i][i] = 1
    }
    
    return I
}

function transpose(A){
    var B = []
    for (var i=0; i<A[0].length; i++){B.push([])}
    for (var i=0; i<A.length; i++){
        for (var j=0; j<A[i].length; j++){B[j][i] = A[i][j]}
    }
    return B
}

function ADI_step(D, Dx, Dt, U){
    var beta = D*Dt/(2*Dx**2)
    var M1 = []
    var M2 = [[]]
    
    for (var i=0; i<U.length; i++){
        M1.push([])
        M2.push([])
        for (var j=0; j<U[i].length; j++){
            M1[i][j]=0
            M2[i][j]=0
        }
        if (i == 0 || i == U.length-1){
            M1[i][i] = 1
            M2[i][i] = 1
        } else {
            M1[i][i-1] = -beta
            M1[i][i+1] = -beta
            M1[i][i] = 1+2*beta
            M2[i-1][i] = beta
            M2[i+1][i] = beta
            M2[i][i] = 1-2*beta
        }
    }
    M2.pop()
    console.log(U)
    var half_step = matmul(td_invert(M1), matmul(U, M2))
    console.log(half_step)
    return matmul(matmul(transpose(M2), half_step), td_invert(transpose(M1)))
}

var kernel = IPython.notebook.kernel;

var D = 1

var T = 5
var adi_size = 21
var Dx = 1
var Dt = .1

var times_adi = [0]
var u_adi = [[]]
for (var k=0; k<adi_size; k++){
    u_adi[0].push([])
    for (var i=0; i<adi_size; i++){u_adi[0][k][i]=0}
}
u_adi[0][Math.floor((adi_size)/2)][Math.floor((adi_size)/2)] = 1

for (var t=Dt; t<=T; t += Dt){
    u_adi.push(ADI_step(D, Dx, Dt, u_adi[u_adi.length-1]))
    times_adi.push(t)
}
console.log(u_adi)
kernel.execute("u_adi = " + u_adi)
kernel.execute("times_adi = " + times_adi)
kernel.execute("adi_lattice_size = " + adi_size)
In [ ]:
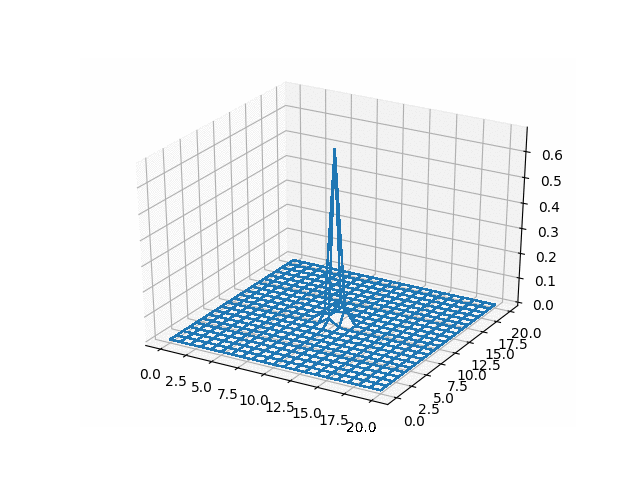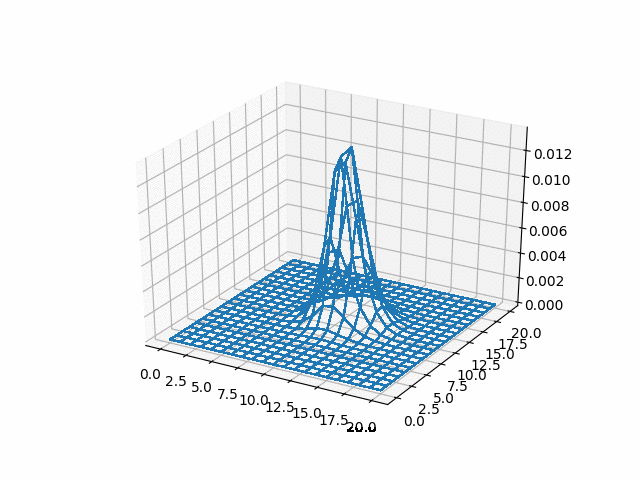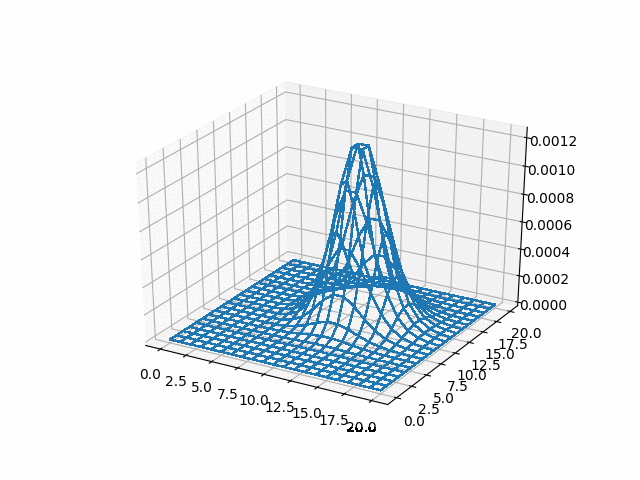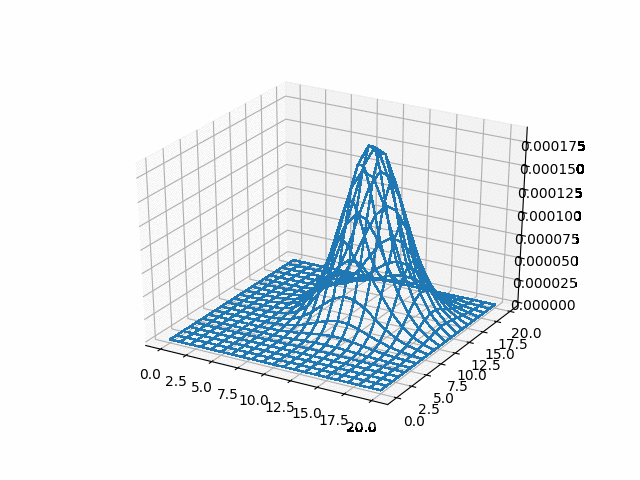
u_adi = np.reshape(np.array(u_adi), (-1, adi_lattice_size, 
                                     adi_lattice_size))
i = 0
X, Y = np.meshgrid(list(range(adi_lattice_size)), 
                   list(range(adi_lattice_size)))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_wireframe(X, Y, u_adi[i],
                         linewidth=1, antialiased=False)

def updatefig(*args):
    global i, surf
    surf.remove()
    surf = ax.plot_wireframe(X, Y, u_adi[i],
                             linewidth=1, antialiased=False)
    i = (i+1) % len(u_adi)
    return surf, 

ani = animations.FuncAnimation(fig, updatefig, np.arange(200), 
                              interval=25, blit=True)
ani.save('gifs/adi.gif', writer='imagemagick', fps=30)
In [3]:
%%html
<img src="gifs/adi.gif">

Problem 8.4

Use SOR to solve Laplace’s equation in $2D$, with boundary conditions $u_{j,1} = u_{1,k} = 0$, $u_{N,k} = −1$, $u_{j,N} = 1$, and explore how the convergence rate depends on $\alpha$, and how the best choice for α depends on the lattice size.

In [ ]: