Problem Set 10 (Functions)

1

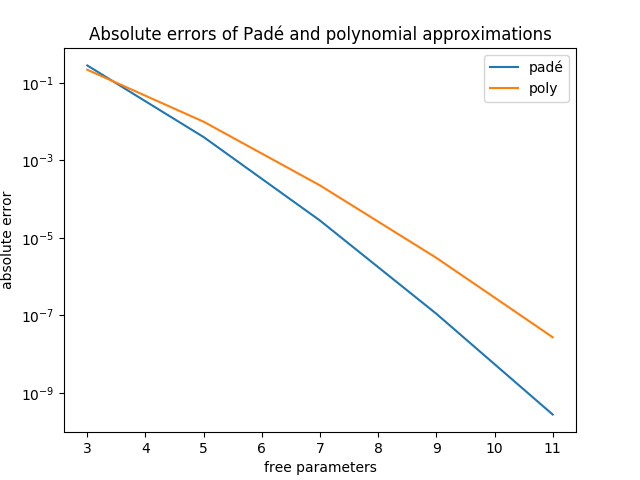
Find the first five diagonal Padé approximants [1/1], …, [5/5] to $e^x$ around the origin. Remember that the numerator and denominator can be multiplied by a constant to make the numbers as convenient as possible. Evaluate the approximations at $x = 1$ and compare with the correct value of $e = 2.718281828459045$ . How is the error improving with the order? How does that compare to the polynomial error?

For a fixed function $f$ and integers $N \geq 0$ and $M \geq 0$ , the Padé approximant is the function

$[N/M]_ f(x) = \frac{\sum_{n = 0}^N a_n x^n}{1 + \sum_{m = 1}^M b_m x^m}$

that matches as many terms as possible of the Taylor series of $f$ . (We can define the approximant about any point, but without loss of generality we’ll only consider the origin.) There are $N + M + 1$ parameters in the formula above ( $a_0$ , $\ldots$ , $b_N$ , and $b_1$ , $\ldots$ , $b_M$ ), so in general this means we can match $f$ up to order $N + M + 1$ . (Though by coincidence, or otherwise, we may end up matching some higher order terms as well.)

We can write the resulting system of equations explicitly by expanding the Taylor series of the approximant to order $L = N + M$ (since this gives us $N + M + 1$ terms). To make the equations simpler to write I will introduce a constant $b_0 = 1$ .

$\frac{\sum_{n = 0}^N a_n x^n}{\sum_{m = 0}^M b_m x^m} = \sum_{l = 0}^L c_l x^l$

Then we multiply by the denominator.

$\begin{aligned} \sum_{n = 0}^N a_n x^n &= \left(\sum_{m = 0}^M b_m x^m \right) \left( \sum_{l = 0}^L c_l x^l \right) \\ &= \sum_{m = 0}^M \sum_{l = 0}^L b_m c_l x^{m + l} \end{aligned}$

By setting the different powers of $x$ equal, this gives us $L + 1 = N + M + 1$ equations.

$\begin{cases} a_n = \sum_{m = 0}^{\min(n, M)} b_m c_{n - m} & \text{for } 0 \leq n \leq N \\ 0 = \sum_{m = 0}^{\min(n, M)} b_m c_{n - m} & \text{for } N < n \leq L = N + M \end{cases}$

We know what $c_0$ , $\ldots$ , $c_L$ are, since they must match the Taylor series of $f$ . (In particular, $c_l = f^{(l)} / l!$ .) So by solving this system of equations we can determine all of the unknown parameters. In particular, the last $M$ equations (i.e. for $N < n$ ) can be solved to determine $b_1$ , $\ldots$ , $b_M$ . Then the first $N + 1$ equations immediately give values for $a_0$ , $\ldots$ , $a_N$ .

The first step can be written as a system of $M + 1$ equations.

$\begin{bmatrix} 1 & 0 & 0 & \cdots & 0 & 0 \\ c_{N + 1} & c_{N} & c_{N - 1} & \cdots & c_{N - M + 2} & c_{N - M + 1} \\ c_{N + 2} & c_{N + 1} & c_{N} & \cdots & c_{N - M + 3} & c_{N - M + 2} \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ c_{N + M - 1} & c_{N + M - 2} & c_{N + M - 3} & \cdots & c_{N} & c_{N - 1} \\ c_{N + M} & c_{N + M - 1} & c_{N + M - 2} & \cdots & c_{N + 1} & c_{N} \\ \end{bmatrix} \begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ \vdots \\ b_{M - 1} \\ b_M \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \\ 0 \end{bmatrix}$

Note that if $N + 1 < M$ , then some upper diagonal chunk of the matrix will be zero, corresponding to those entries where the subscript of $c$ would be negative.

Finally, there’s no guarantee that this matrix will be nonsingular. (For example, consider the case where $N = M$ and all derivatives of $f$ up to $N + M$ are zero. Then all rows of the matrix except for the first will be zero.) In such a situation, one can try to throw out degenerate equations, and pull new ones from higher order terms (i.e. consider $L > N + M$ ). However it’s possible that all additional rows will be degenerate; in this case, the approximant is legitimately underdetermined. This means it can match the function exactly, and you can reduce $M$ until your system is nonsingular.

Ok, so now to actually answer the question. I wrote a SymPy script that uses the strategy we just derived to build approximants for me. For $f(x) = e^x$ , I get the following approximations:

$\begin{aligned} [1/1]_ f(x) &= \frac{1 + x/2}{1 - x/2} \\ [2/2]_ f(x) &= \frac{1 + x/2 + x^2/12}{1 - x/2 + x^2/12} \\ [3/3]_ f(x) &= \frac{1 + x/2 + x^2/10 + x^3/120}{1 - x/2 + x^2/10 - x^3/120} \\ [4/4]_ f(x) &= \frac{1 + x/2 + 3x^2/28 + x^3/84 + x^4/1,680}{1 - x/2 + 3x^2/28 - x^3/84 + x^4/1,680} \\ [5/5]_ f(x) &= \frac{1 + x/2 + x^2/9 + x^3/72 + x^4/1,008 + x^5/30,240}{1 - x/2 + x^2/9 - x^3/72 + x^4/1,008 - x^5/30,240} \\ \end{aligned}$

These give the corresponding approximations for $e$ :

$\begin{aligned} [1/1]_ f(1) &= 3 &= 3.00000000000000 \\ [2/2]_ f(1) &= \frac{19}{7} &\approx 2.71428571428571 \\ [3/3]_ f(1) &= \frac{193}{71} &\approx 2.71830985915493 \\ [4/4]_ f(1) &= \frac{2,721}{1,001} &\approx 2.71828171828172 \\ [5/5]_ f(1) &= \frac{49,171}{18,089} &\approx 2.71828182873569 \end{aligned}$

Polynomial approximations, on the other hand (to equivalent orders), give

$\begin{aligned} \sum_{n = 0}^2 \frac{x^n}{n!} &= \frac{5}{2} &= 2.50000000000000 \\ \sum_{n = 0}^4 \frac{x^n}{n!} &= \frac{65}{24} &\approx 2.70833333333333 \\ \sum_{n = 0}^6 \frac{x^n}{n!} &= \frac{1,957}{720} &\approx 2.71805555555556 \\ \sum_{n = 0}^8 \frac{x^n}{n!} &= \frac{109,601}{40,320} &\approx 2.71827876984127 \\ \sum_{n = 0}^{10} \frac{x^n}{n!} &= \frac{9,864,101}{3,628,800} &\approx 2.71828180114638 \end{aligned}$

Here are the different errors.

errors

3

Train a neural network on the output from an order 4 maximal LFSR and learn to reproduce it. How do the results depend on the network depth and architecture?

I have previously implemented backpropagation from scratch, to train my own VAEs. So rather than write this again, I wrote up a better derivation of backpropagation which I can use a reference for future modifications.