Comparing Finite Difference Time Domain and Cellular Automata models for 2D wave simulation

The Video above is a FDTD based simulation of a wave propagating through a mesh (based in javascript - can be found here. This project has, as of yet a large performance issue for which I tried to evaluate if a CA based simulation would alleviate some of these issues. Below are the basis for the above simualtion plus a CA based alternative in python to pit their performance against each other.

This is the structure used in the above video (mesh deformed with Three.js) based in the $H_z$ output.

$$E^{n+1}_x(i,j) = E^{n-1}_x(i,j) + C_H * (E^n_z(i,j+1) - E^n_z(i,j-1))$$$$E^{n+1}_y(i,j) = E^{n-1}_y(i,j) + C_H * E^n_z(i+1,j) - E^n_z(i-1,j)$$$$H^{n+1}_z(i,j) = H^{n-1}_z(i,j) + C_E *(E^n_y(i+1,j) - E^n_y(i-1,j) - E^n_x(i,j+1) - H^n_x(i,j-1))$$

The implementation below is translated to Python from Javascript to use as a base for comparison to the CA based model.

import matplotlib
import matplotlib.pyplot as plt
import matplotlib.animation as animation
%matplotlib notebook
import numpy as np
from matplotlib import rc
rc('animation', html='html5')

C = 343 #m/s = speed of sound
CA_DX = 0.001 #m = cell size
CA_DT = 1/C 

size_x = 100
size_y = 100
pos_x = int(size_x/2)
pos_y = int(size_y/2)

measure_x = int(size_x/4) 
measure_y = pos_y
measure_x2 = int(size_x-(size_x/4))

min_pressure = -0.3
max_pressure = 0.3


# epsilon
eps = np.ones((size_x, size_y))

#initialize fields
Ex = np.zeros((size_x, size_y))
Ey = np.zeros((size_x, size_y))
Hz = np.zeros((size_x, size_y))

#spatial steps
dx = dy = 1

#time steps
tsteps = 100
dt = 1
c = 1
## courant constant
#cc = c*dt/min(dx, dy)
cc = 0.5
d = 0.99

def calculate(t, Ex, Ey, Hz):
    print('t= '+str(t))
    #update Hz, Ex, Ey
    # update H field components
    deriv_y = np.zeros((size_x, size_y))
    deriv_x = np.zeros((size_x, size_y))
    for j in range(size_x):
        for k in range(size_y):
            indx = j + 1; indy = k + 1
            if (indx > size_x - 1):
                indx = 0
            if (indy > size_y - 1):
                indy = 0
            deriv_y[k, j] = (Ex[indy, j] - Ex[k, j])
            deriv_x[k, j] = (Ey[k, indx] - Ey[k, j])
    Hz -= (deriv_x - deriv_y)
    Hz[int(size_x/2), int(size_y/2)] -= 2*np.sin(2*np.pi*t/10)*(dt)


    #update E field components
    Curl_x = np.zeros((size_x, size_y))
    Curl_y = np.zeros((size_x, size_y))
    
    for j in range(size_x): #y axis
        for k in range(size_y): #x axis
            indx = j - 1; indy = k - 1
            if(indx < 0):
                indx = size_x - 1
            if(indy < 0):
                indy = size_y - 1
            deriv_y = -(Hz[indy, j] - Hz[k, j])
            deriv_x = -(Hz[k, indx] - Hz[k, j])
            Curl_x[k, j]= (cc) * d * (deriv_x) 
            Curl_y[k, j] = (cc) * d * (deriv_y)  
    Ex += Curl_y
    Ey -= Curl_x
    
fig = plt.figure(figsize=(6,6))
fdtd_plot = plt.imshow(Ey, cmap='jet', interpolation='bilinear', vmin=min_pressure, vmax = max_pressure)
plt.colorbar(fdtd_plot)


def animate(i):
    calculate(i, Ex, Ey, Hz)
    fdtd_plot.set_data(Hz)
    return fdtd_plot

anim = animation.FuncAnimation(fig, animate, frames=size_x, interval=1)
plt.show()

Cellular Automata Model

The local interaction rules for particle velocity and pressure in all four directions ("cell neighbors") from our momentary cell in our Cellular Automata (CA) model are as follows:

$$V_i'(x,t+1) = V_i(x,t) − {P(x + dx_i,t) − P(x,t)}$$

$V_i$ represents the particle velocity in each cell. $P$ denotes the sound pressure. The two dimensional cell position is expressed as the vector $x$.

For this test the particle velocity also obeys linear energy dissipation:

$$V_i(x,t+1) = (1 - d) * V_i'(x,t+1)$$

Here $d$ serves as the damping constant per cell assuming slight absorption my the air. In this case we use 0.001 for $d$ to add a little damping effect.

The pressure needs to be updated according to the following rule:

$$P(x,t+1) = P(x,t) - c^2_i \sum_i V_i(x,t+1)$$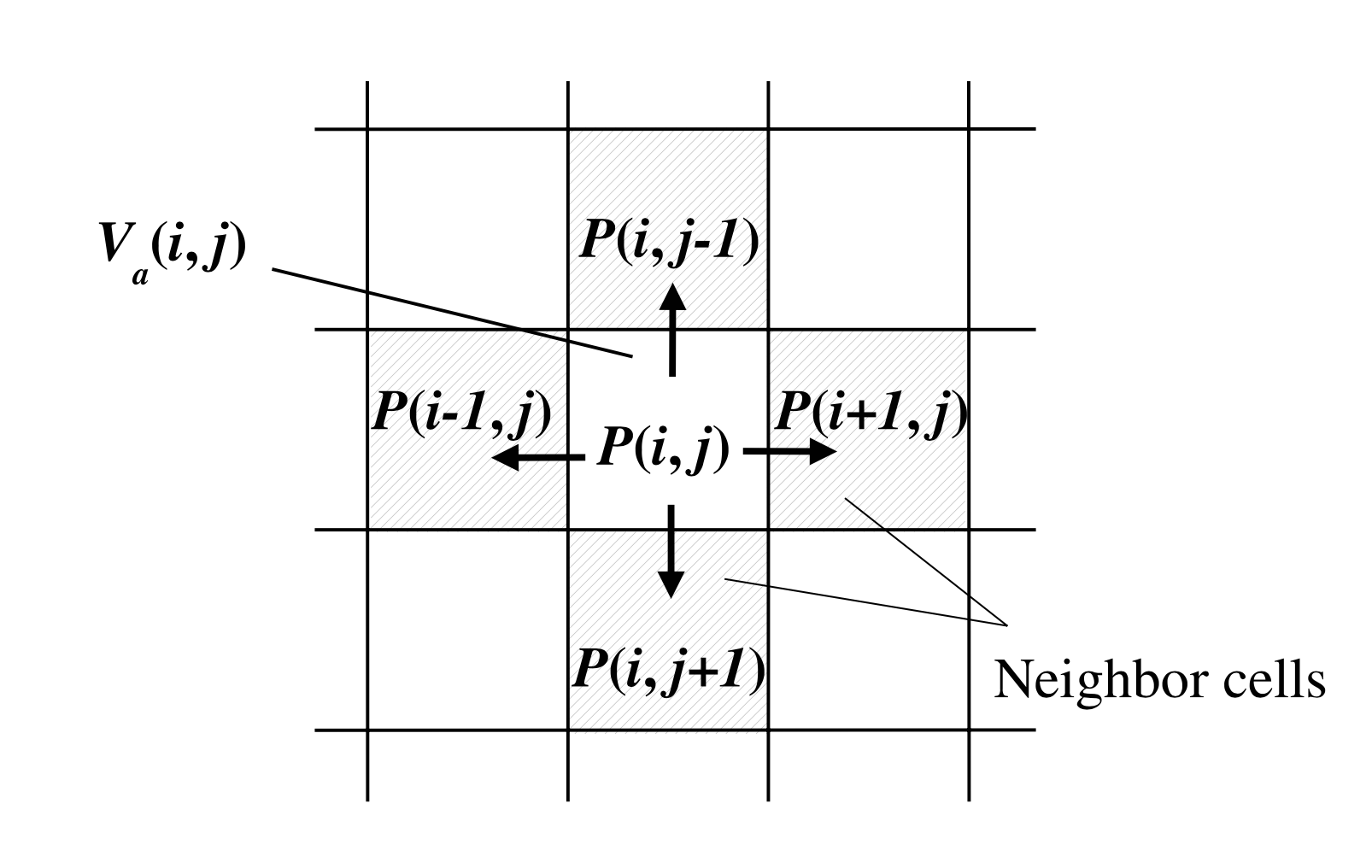

Above: Definition of neighboring cells in the two dimensional model [1]

CA Implementation

damping = 0.99
omega = 3 / (2 * np.pi)

freq = C/(4*size_x) # standing wave for closed cylinder
amplitude = 1 
wavelength = 4*size_x


# update rules for pressure and velocity based on neighbouring cells
pressure = [[0.0 for x in range(size_x)] for y in range (size_y)]
V = [[[0.0, 0.0, 0.0, 0.0] for x in range(size_x)] for y in range (size_y)]
c = 1 / np.sqrt(2) 

measure = []
measure2 = []

def update_V():
    # V(x,dt) = V(x,t) - {P(x + dx, t) - P(x,t)} 
    for i in range(size_y):
        for j in range(size_x):
            #p = pressure;
            #V = velocity
            cell_pressure = pressure[i][j]
            V[i][j][0] = V[i][j][0] + cell_pressure - pressure[i - 1][j] if i > 0 else cell_pressure
            V[i][j][1] = V[i][j][1] + cell_pressure - pressure[i][j + 1] if j < size_x -1 else cell_pressure
            V[i][j][2] = V[i][j][2] + cell_pressure - pressure[i + 1][j] if i < size_y -1 else cell_pressure
            V[i][j][3] = V[i][j][3] + cell_pressure - pressure[i][j - 1] if j > 0 else cell_pressure
            
def update_P():
    for i in range(size_y):
        for j in range(size_x):
            pressure[i][j] -= c**2 * damping * sum(V[i][j])
            
def step(i):
    pressure[pos_y][pos_x] = amplitude * np.sin(freq/10 * 2 * np.pi * i)
    update_V()
    update_P()
    
figure = plt.figure(figsize=(6,6))
ca_plot = plt.imshow(pressure, cmap='jet', interpolation='bilinear', vmin=min_pressure, vmax = max_pressure)
plt.colorbar(ca_plot)

def anim(i):
    step(i)
    ca_plot.set_data(pressure)
    return ca_plot

anim = animation.FuncAnimation(figure, anim, frames=100, interval=1)
plt.show()

Since the topmost simulation has memory and performance issues the goal was to see if the CA algorithm would be a better choice to deform the mesh to save up some performance for the to-be-changed sound synthesis.

Therefore the time it takes each algorithm to advance through 100 steps was recorded for several grid sizes with the following results (codes used for time measuring without any visual output can be found here) :

Grid Size	FDTD	CA
10 x 10	0.0397	0.036
20 x 20	0.162	0.147
30 x 30	0.349	0.3195
40 x 40	0.615	0.587
50 x 50	1.078	0.897
100 x 100	3.973	3.674
200 x 200	15.456	14.958
500 x 500	98.043	96.791
1000 x 1000	400.182	385.934

Conclusion

The above table and the two animations show that the performance increase from a FDTD to CA based model is only a slight improvement of roughly 0.96 times the duration it takes the FDTD model to calculate 100 steps. Over the tested grid size the difference between performance for both remains fairly constant (larger grid sizes remain to be tested).