

(a) Work out the first three cumulants C1, C2, and C3.
\[exp\left(\sum_{n=1}^{\infty}\frac{(ik)^n}{n!}C_n\right) = \sum_{n=0}^{\infty}\frac{(ik)^n}{n!}\langle x^n \rangle\] \[1 + \left(\sum_{n=1}^{\infty}\frac{(ik)^n}{n!}C_n\right) + {\left(\sum_{n=1}^{\infty}\frac{(ik)^n}{n!}C_n\right)^2}/{2!} + {\left(\sum_{n=1}^{\infty}\frac{(ik)^n}{n!}C_n\right)^3}/{3!}\] First order term of \(k\): \[iC_1 = i\langle x \rangle \Rightarrow C_1 = \langle x \rangle\] Second order term of \(k\): \[-\frac{C_2}{2} - \frac{C_1^2}{2} = -\frac{1}{2} \langle x^2 \rangle \Rightarrow C_2 = \langle x^2 \rangle - {\langle x \rangle}^2\] Third order term of \(k\): \[-\frac{i}{6}C_3 - \frac{i}{6}C_1^3 = -\frac{1}{6} i \langle x^3 \rangle \Rightarrow C_3 = \langle x^3 \rangle - {\langle x \rangle}^3\]
(b) Evaluate the first three cumulants for a Gaussian distribution \[p(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-(x-\bar{x})^2/{2\sigma^2}}\]
(a) If \(\vec{y}(\vec{x}) = (y_1(x_1,x_2),y_2(x_1,x_2))\) is a coordinate transformation, what is the area of a differential element \(dx_1 dx_2\) after it is mapped into the \(\vec{y}\) plane? Recall that the area of a parallelogram is equal to the length of its base times its height.
\[b = \vec{y}(x_1+dx_1, x_2)-\vec{y}(x_1,x_2) = \frac{\partial{\vec{y}}}{\partial{x_1}} \cdot dx_1\] \[h = \vec{y}(x_1,x_2+dx_2)-\vec{y}(x_1,x_2) = \frac{\partial{\vec{y}}}{\partial{x_2}} \cdot dx_2\] \[ \Rightarrow A = b \cdot h = \left(\frac{\partial{\vec{y}}}{\partial{x_1}} \cdot dx_1\right)\left(\frac{\partial{\vec{y}}}{\partial{x_2}} \cdot dx_2\right) \]
(b) Let \[y_1 = \sqrt{-2lnx_1} sin(x_2)\] \[y_2 = \sqrt{-2lnx_1} cos(x_2)\] If \(p(x_1, x_2)\) is uniform, what is \(p(y_1,y_2)\)?
Jacobian matrix \[\begin{align*}\mathbf{J} & = \begin{bmatrix} \dfrac{\partial{y_1}}{\partial{x_1}} & \dfrac{\partial{y_1}}{\partial{x_2}} \\ \dfrac{\partial{y_2}}{\partial{x_1}} & \dfrac{\partial{y_2}}{\partial{x_2}} \end{bmatrix} \\& = \begin{bmatrix} -\dfrac{sin(x_2)}{2x_1\sqrt{-2lnx_1}} & \sqrt{-2lnx_1}cos(x_2) \\ \dfrac{cos(x_2)}{2x_1\sqrt{-2lnx_1}} & -\sqrt{-2lnx_1}sin(x_2) \end{bmatrix} \\ det(\mathbf{J}) & = \frac{sin^2(x_2)}{2x_1}-\frac{cos^2(x_2)}{2x_1} \end{align*} \]
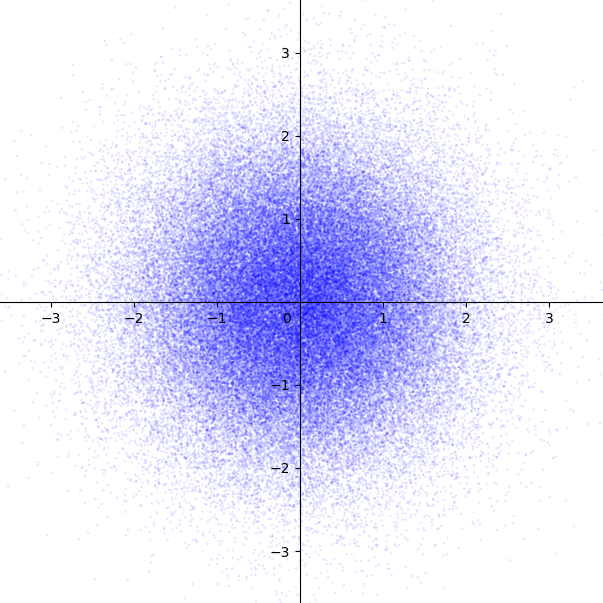
(c) Write a uniform random number generator, and transform it by equation. Numerically evaluate the first three cumulants of its output.
Let's zoom in a little bit...
(a) For an order 4 maximal LFSR write down the bit sequence.
(b) If an LFSR has a clock rate of 1 GHz, how long must the register be for the time between repeats to be the age of the universe (~ \(10^{10}\) years)?
(a) Use a Fourier transform to solve the diffusion equation (6.57) (assume that the initial condition is a normalized delta function at the origin).
(b) What is the variance as a function of time?
(c) How is the diffusion coefficient for Brownian motion related to the viscosity of a fluid?
(d) Write a program (including the random number generator) to plot the position as a function of time of a random walker in 1D that at each time step has an equal probability of making a step of ± 1. Plot an ensemble of 10 trajectories, each 1000 points long, and overlay error bars of width \(3\sigma(t)\) on the plot.
(e) What fraction of the trajectories should be contained in the error bars?