import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
fig, ax = plt.subplots()
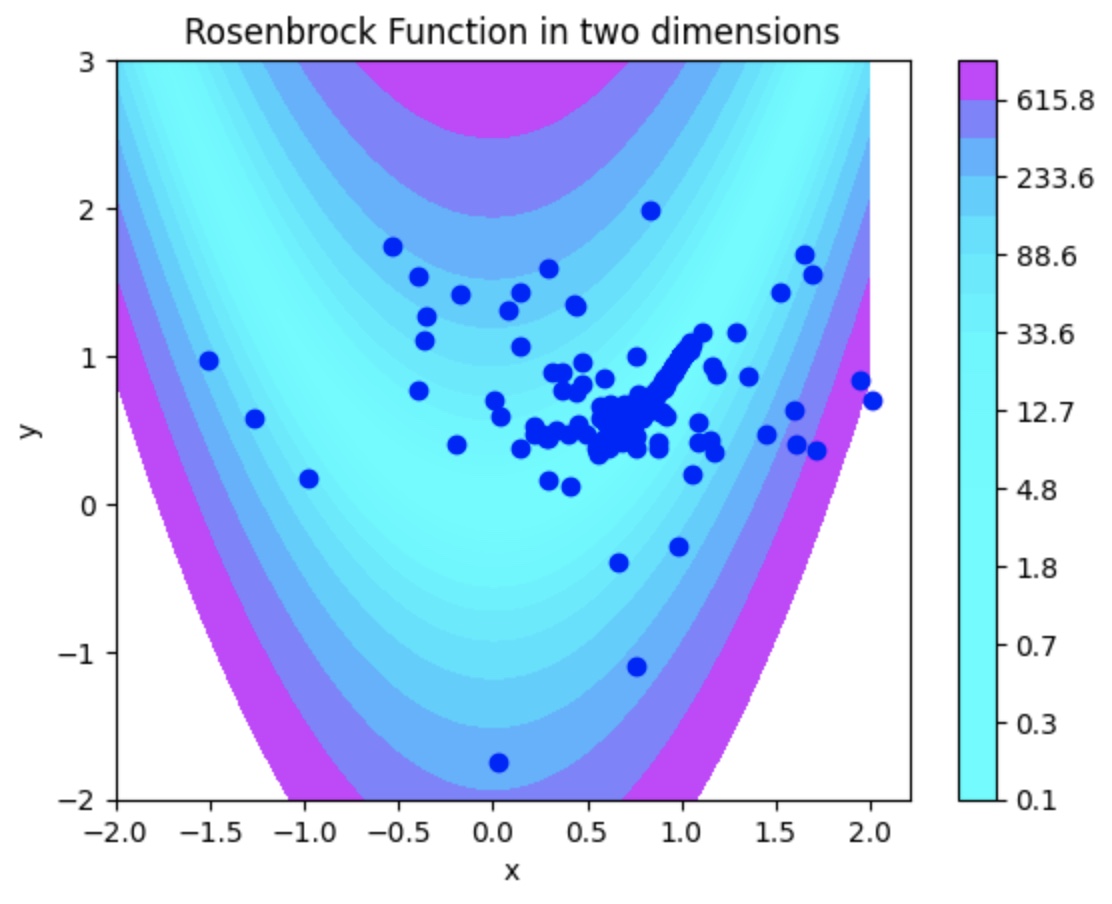
def rosenbrock(x, y):
return (1-x)**2 + 100*(y-x**2)**2
plot_x = np.linspace(-2, 1, 100)
plot_y = np.linspace(-2, 3, 100)
X, Y = np.meshgrid(plot_x, plot_y)
Z = rosenbrock(X, Y)
# Create simplex vertices (three points)
'''
Method 1 - all points separate. Drawback is that it doesn't scale to more dimensions.
x1 = np.array([-1, -1], dtype=float) # Given by Neil
x2 = np.array([0, -1], dtype=float)
x3 = np.array([-1, 0], dtype=float)
vertex_list = [x1, x2, x3]'''
# Method 2 - all points in one array. Better on the long run.
simplex_vertices = np.array([
[-1, -1], # Starting point given by assignment
[ 0, -1],
[-1, 0],
], dtype=float)
# First point
print(simplex_vertices[0])
# Second point
print(simplex_vertices[1])
# Third point
print(simplex_vertices[2])
# Gives first column of the matrix
print(simplex_vertices[:,0])
'''
Notes:
Before colon is row
After colon is column
'''
# Colormap settings
# levels = [1e-2, 1e-1, 1e0, 1e1, 1e2, 1e3, 1e4, 1e5]
cmap = mpl.cm.cool # Setting the color
norm = mpl.colors.Normalize(vmin=None, vmax=None) # Setting to none, to map the values.
contour = ax.contourf(X, Y, Z, levels=np.logspace(-1, 3, 20), cmap=cmap, norm=norm)
cbar = plt.colorbar(contour, ticks=[1e0, 1e1, 1e2, 1e3])
# Plotting
plt.scatter(simplex_vertices[:,0], simplex_vertices[:,1], color='blue', marker='x')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Rosenbrock Function')
plt.show()