<br>
[MAS.865](../../index.html) > [Mechanisms](../../Mechanisms) > Flexures
##Preliminaries
Flexures are complaint structures which provide degrees of freedom in certain prescribed directions. Their motion is not rigid, though flexural motion are often close enough to rigid motion to be approximated as such for performing tasks such as kinematics. However, flexural dynamics, as well as the more detailed nuances of their motion are different, and deserve attention. It should be noted that most flexures (non-plastic ones) have a "spring-like" quality to them, deforming under loads but returning to a rest configuration when the load is removed.
Flexural analysis typically comes in two flavors. The first makes certain assumptions to achieve closed-form approximations. The second uses simulation in order to analyze arbitrary structures.
##Closed-Form Analysis
An excellent summary can be found <a href="http://web.mit.edu/mact/www/Blog/Flexures/FlexureIndex.html">here</a>. Analysis is grounded in the bending beam equation.
##Finite Element Analysis
Finite Element Analysis (FEA), also known as the Finite Element Method (FEM) provides a good means for understanding flexures with more complex geometry. FEM breaks larger geometry scturctures up into small elements, which, in 2D, may be rectangles, triangles, or more complex shapes, and in 3D, may be tetrahedra, cuboids, or other more complex shapes. Each of these small shapes is an "element."
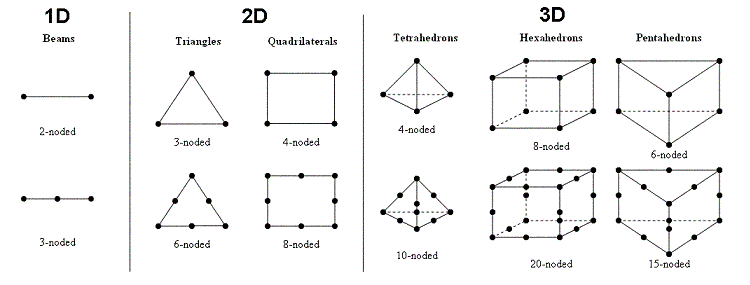
Physically, each element is approximated as a linear or nonlinear spring, parameterized by a material's Young's Modulus (elasticity) and Poisson Ratio (compressability). In the finite element method, mass is distributed along shape vertices. In the limit that the elements become infinitessimally small (and their count, infinitely large), the finite element method approximates the continuum dynamics of the structure. Having many elements will lead to a high computational overhead though, and so smaller element count approximations usually suffice.

In the finite element method, a "tangential stiffness matrix" is formulated for any particular element coordinates u. In the absence of other dynamical phenomena, the equations of motion then become:
$$ M \ddot{x} = Kx - F $$
where M is the mass matrix and F are the loading forces.
Such dynamics can also be approximated using "linear modes," which will be covered in another lecture.
[We can apply this to planar compliant mehchanism design with discrete parts](http://www.willlangford.me/labs/mechsim/)
##Simple Examples
### Pin Flexures

### Blade Flexures
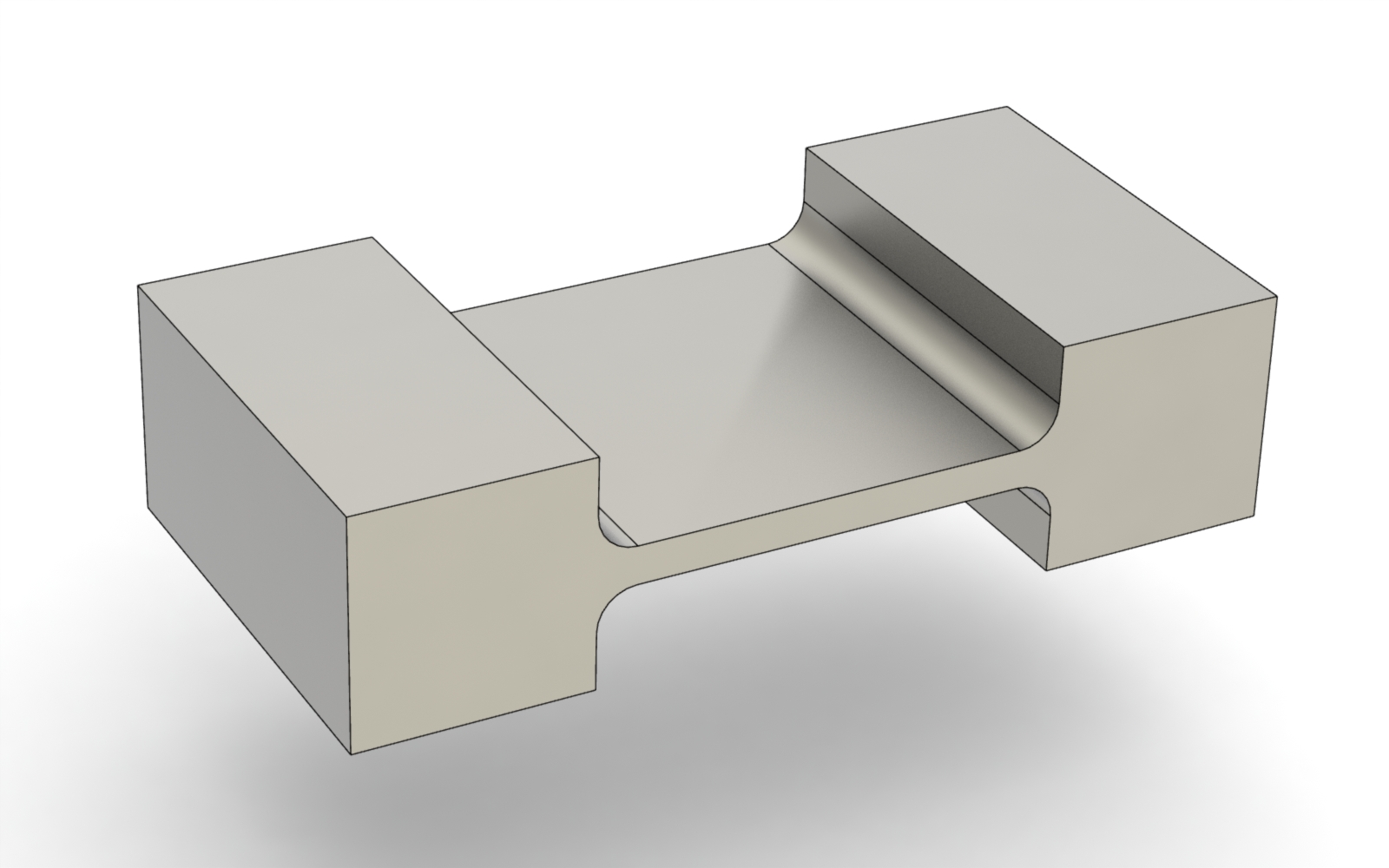
### Notch Flexures
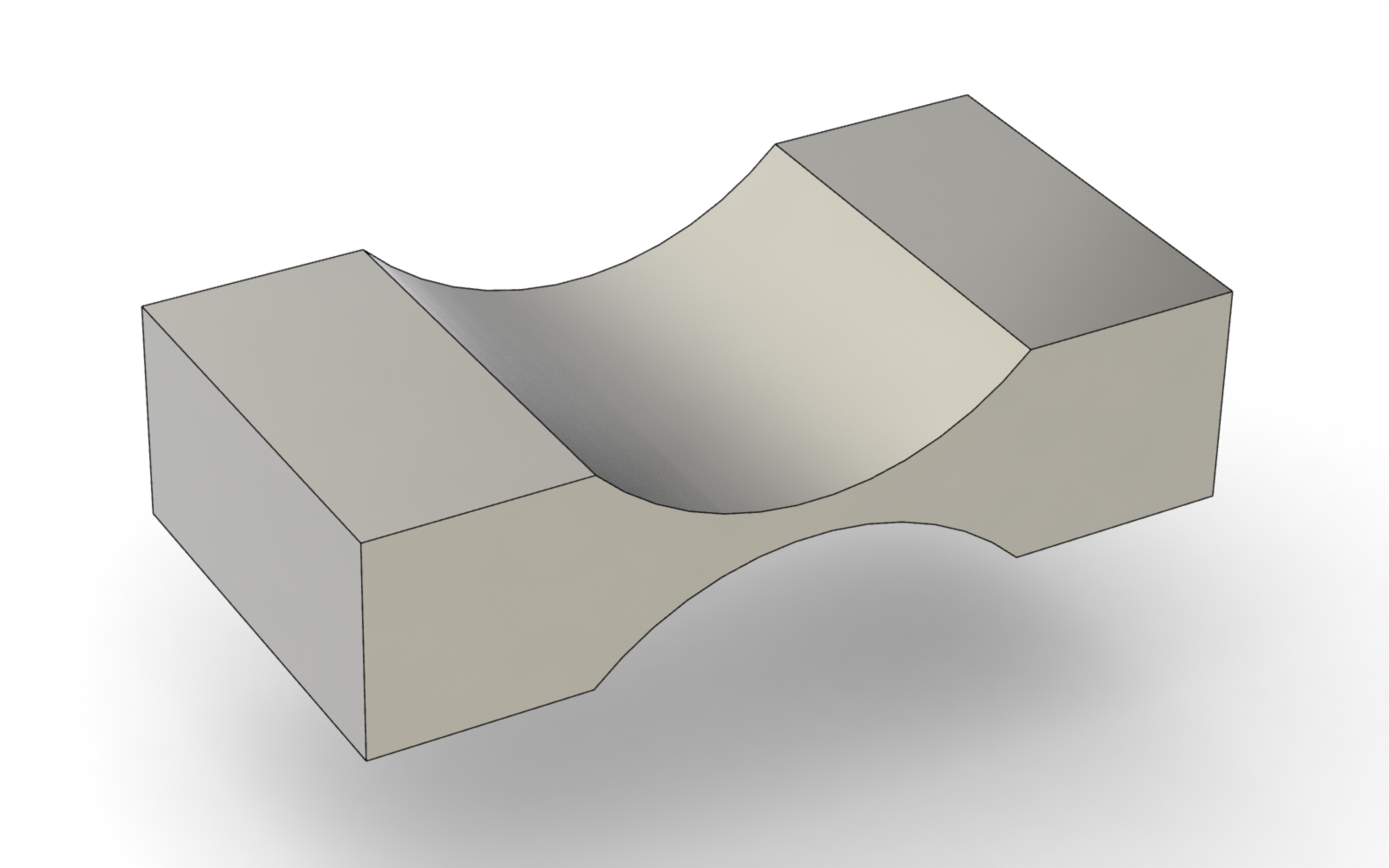
### Living Hinge
Living hinges are flexures constrained to create single-degree of freedom hinges. Since they are made out of "springy" materials, they tend to have a default, minimum energy rest state to which they'll return, and force is needed to move them away. The possible motions approximate that of a revolute joint.

<a href="http://mtm.cba.mit.edu/machines/deploy/index.html"><img src="http://mtm.cba.mit.edu/machines/deploy/img/grass.jpg" width="500px"></a>
##Design
In general, one wants to design flexures that can achieve a desired range of kinematic motions. There are many well known typologies for doing this, and many research approaches for optimizing flexure design.
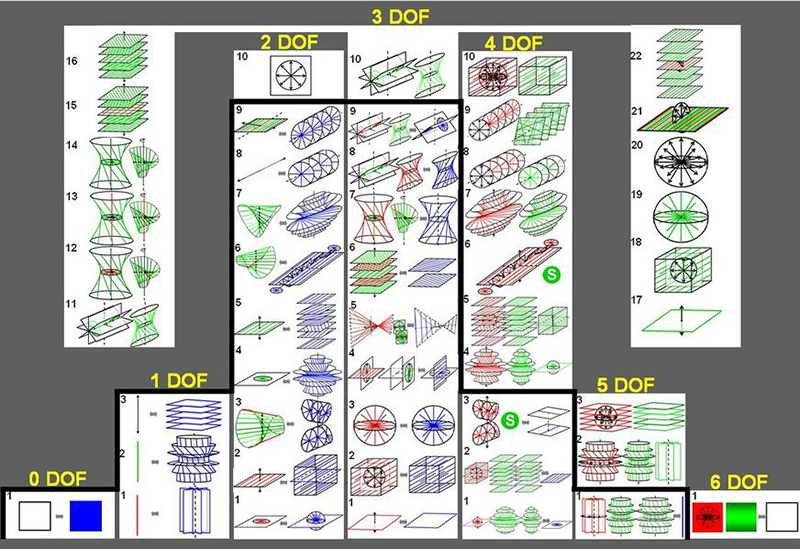
###Auxetics:


###Compliant Hinge Design:
Compliant Mechanism Design
<video controls src="compliant.mp4" width="640"></video>
Laser Cut Living Hinges:
<a href = "https://www.ponoko.com/blog/how-to-make/how-to-design-a-living-hinge"/>Laser Cut Design</a>


###Kinematic-Based Design:
##Flexural Systems
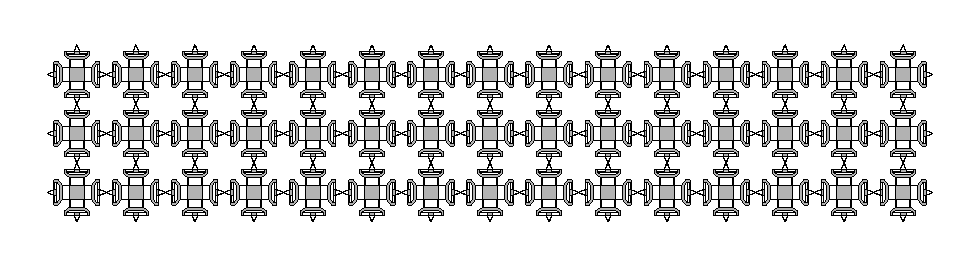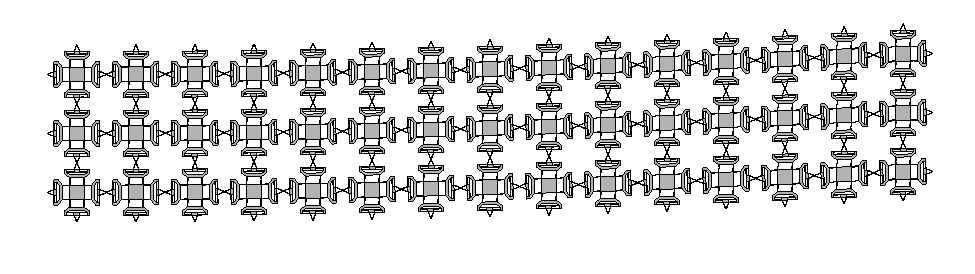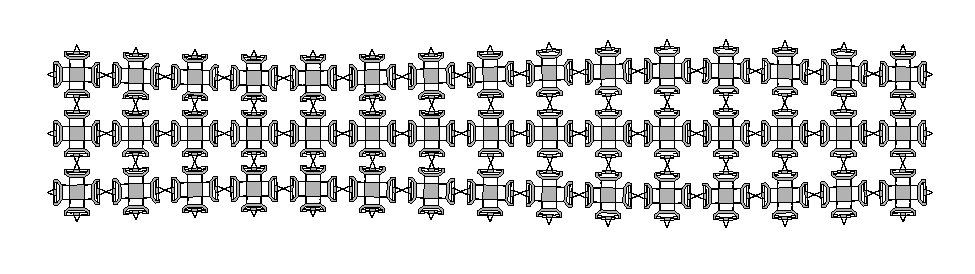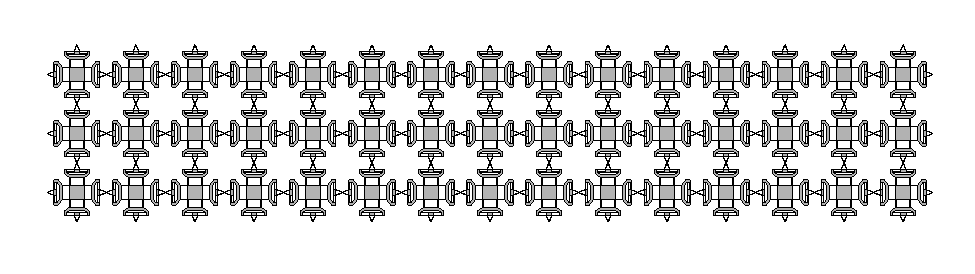
<a href = "http://cba.mit.edu/projects/dma/assembled_assemblers/index.html">Assembly Based Flexure Construction</a>
<a href = "https://robotics.eecs.berkeley.edu/~ronf/Prototype/index.html">Flexural-based Folded Robots</a>
Which led to a product:
<a href = "http://kamigamirobots.com/">Kamigami Robots</a>
<a href="https://wyss.harvard.edu/technology/pop-up-mems/">Pop-Up MEMS</a>.
Pop-Up Robots:
<!-- <video controls src="robots.mp4" width="640"></video> -->
<iframe width="640" height="360" src="https://www.youtube.com/embed/VxSs1kGZQqc" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe>
<a href="http://www.popupcad.org/">Pop-Up CAD</a>.
<a href = "https://ppm.csail.mit.edu/sites/default/files/publications/jmr_007_02_021012.pdf">Foldable Joints for Foldable Robots</a>.
[Assembled compliant mechanisms](mechanism_petting_zoo.html)