<br>
[MAS.865](../../index.html) > [Mechanisms](../../Mechanisms) > Linkage Mathematics
##Preliminaries
Linkages are mechanical constructs which can convert one type of input motion into another type of output motion. This is performed by connecting rigid bodies together in such a way that at least <i>one</i> (and typically exactly one) degree of freedom (DoF) is left remaining. This one DoF can be connected to an actuator and driven to perform tasks. Rigid bodies in a linkage are typically connected together using revolute joints, though this need not always be the case.
A rigid body in the world has 6 degrees of freedom (x, y, z, roll, pitch, and yaw). Thus, a system with n links normally would have 6n degrees of freedom. However, each joint connection constrains degrees of freedom, bringing the total number down to a number that is much less. Each revolute (rotational) or prismatic (sliding) joint adds 5 constraints, reducing the number of degrees of freedom by 5. For example, a revolute joint glues the x, y, and z positions on two links together, and constraints two rotational degrees of freedom. Other joints, such as ball-and-socket joints, reduce the number of degrees of freedom by 3 (gluing two bodies in x, y, and z). The total number of degrees of freedom of a linkage with n links and m joints is simply:
$$DoF(linkage) = 6n - \sum_{i=1}^{m} DoF(i)$$
where DoF(i) is the number of degrees of freedom of joint i. The Chebychev–Grübler–Kutzbach criterion gives an equivalent way to compute the degrees of freedom of a linkage, using the number of constraints imposed instead.
##Linkage Types
There are two types of linkages: open and closed linkages. First, a definition: a kinematic graph is a graphical (in the discrete mathematical sense) representation of a linkage, in which links are nodes and joints are edges connecting the nodes corresponding to the links the physical joint connects.
Open linkages, also known as kinematic trees, have a kinematic graph which is a tree.
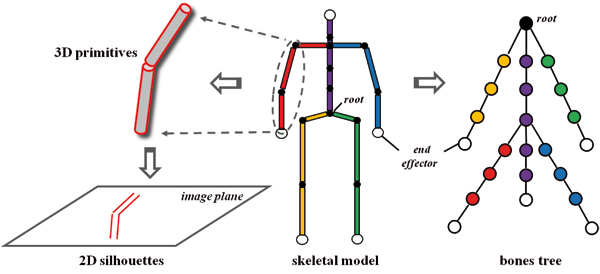
If each node has at most two incident edges, then the graph is a linked list. In this case, the linkage is also called a <i>kinematic chain</i>.
Closed linkages, meanwhile, have a kinematic graph which is <i>not</i> a tree (even DAGs are not open).
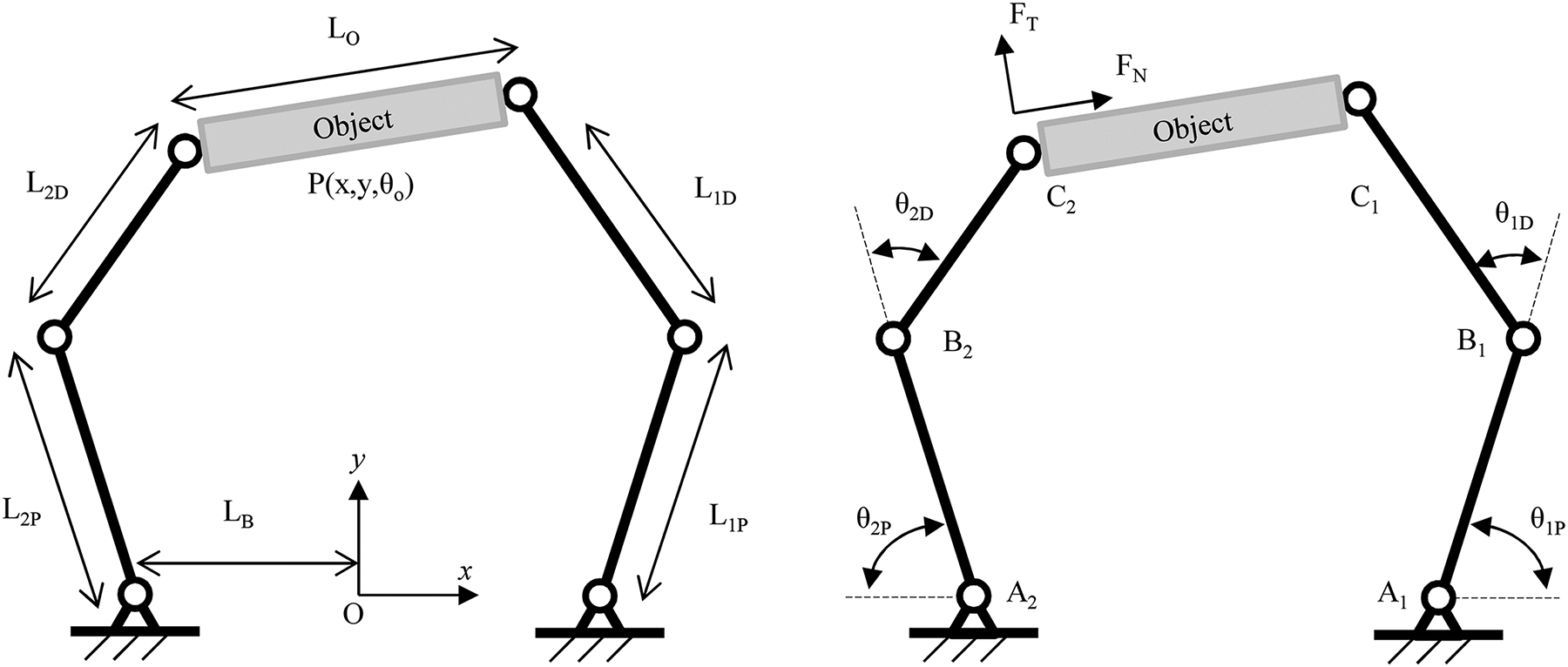
##Linkage Computation
There are two classical tasks one wishes to perform with linkages - forward kinematics and inverse kinematics. The means of performing these is different for each class of linkage (open or closed).
Forward kinematics is the task of transforming a point in the frame of a rigid body to the world frame, given the linkage's joint configuration. Inverse kinematics is the task of determining the joint configuration which can put a point in the frame of a rigid body at a target world position.
In other words:
Forward kinematics: Input - joint configuration - Output - point in world.
Inverse kinematics: Input - point in world - Output - joint configuration.
We now discuss the computation for each of the four cases in turn.
#### Open Linkage - Forward Kinematics
Use recursive linear algebra. Note that the global positiion x of any point p on a single rigid body can be written as an affine transform:
$$x = R_ip + T_i$$
where, for rigid body i, T_i represents the link's global translation, and R_i represents its global rotation. We can write this more compactly as the homogeneous transform H_i,
$$\begin{bmatrix}R_i & T_i \\\\ 0 & 1\end{bmatrix}$$
$$(R_i = 3 \times 3, T_i = 3 \times 1, 0 = 1 \times 3, 1 = 1 \times 1)$$
If we then change the definition of R_i and T_i to be the rotation and translation of a link with respect to its parent link (as defined by the kinematic graph), we can write the position of any point as:
$$ H_0 H_1 \ldots H_n p $$
where the subscripts index the respective homogenous transforms along a path from a link to the root. This is general recursive formula for computing forward kinematics.
#### Open Linkage - Inverse Kinematics
One other way to approach forward kinematics is to formulate the Jacobian matrix. The Jacobian is the gradient of the world coordinates of a point on a kinematic tree with respect to its joint configuration. If the tree has $m$ joints and exists in $k$ dimensional space, then the Jacobian J is a k by m matrix:
$$ J_{i, j} = \frac{\partial x_i}{\partial \phi_j} $$
$$(x = \text{world point}, \phi = \text{joint configuration})$$
If we compute the product of J with the joint configuration vector, we get the position of a point on the tree in world coordinates. This transformation is unique.
The inverse mapping is typically not, since the Jacobian matrix may be rank deficient, but it can be computed by solving the system in the least squares sense. Trajectories, likewise, can be solved by minimizing individual problems in the least squares sense, and formulating an outer optimization problem which promotes smoothness between poses.
#### Closed Linkage Kinematics
Even though the linkage is closed, solving kinematics ironically does not have a closed form. Since the number of constraints outnumber the number of joint degrees of freedom in the system (caveat: this is for linkages with joint DoF = 1), kinematic simulation typically must be achieved by attempting to solve a number of constraint simultaneously.
One prescription for this is to attempt to solve a nonlinear least-squares problem. Let c_ij be a constraint that connects links i and j at a point for revolute joints, or along a line with fixed orientation for prismatic joints. We will focus on revolute joints for now. For a revolute joint, note that c_ij can be written as :
$$x_i - x_j = 0$$
In this scenario, we represent each link in terms of its global position and orientation, rather than use the parameterization of the joint (at the end, we can always go back and calculate the joint angles).
Then, we solve a nonlinear least squares problem:
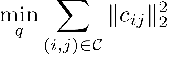
here, q is the vector representing all degrees of freedom of links, and C is the set of constraints. If one wants to prescribe fixed joint angles, or fixed positions of points on links, these can be added either as linear constraints or by directly substituting in fixed values of certain q coordinates.