Principles:
A machine’s mechanical embodiment is where our computers (microcontrollers and otherwise) meet the physical world, and the better we do to make that linkage linear, smooth and predictable the better our assembly (controller and mechanism) will perform. Control experts will remind you that a good plant with a first-order model will often do better than a shoddy one with a third-order model or better.
Stiffness
Understanding the subtlety of stiffness is probably the most important element you can take away from this section of machine class. The idea of ‘stiffness’ will turn up throughout, so I need to start here.
Stiffness is simply the way an object resists deformation in response to an applied force so, how much something bends when we push on it. Machine design asks us to consider even very small deflections - hundredths of mm or less. This is why the use of castings are so common in heavy machinery: there is no better solution for stiffness than to add steel / iron to a structure: the balance is in reducing weight, so that our machines do not require infinite energy to move about.
For materials, stiffness is the slope of a stress-strain plot:
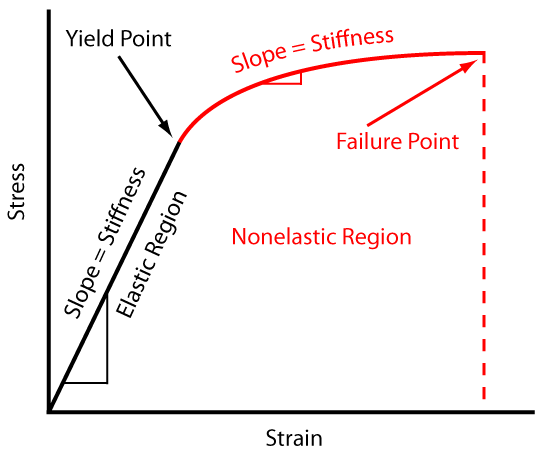
But stiffness is not just a property of materials, it is a property of complete structure, or can be a property of some component, for example, linear ways are rated in N / um - the force required to deflect them by one thousandths of a millimeter.
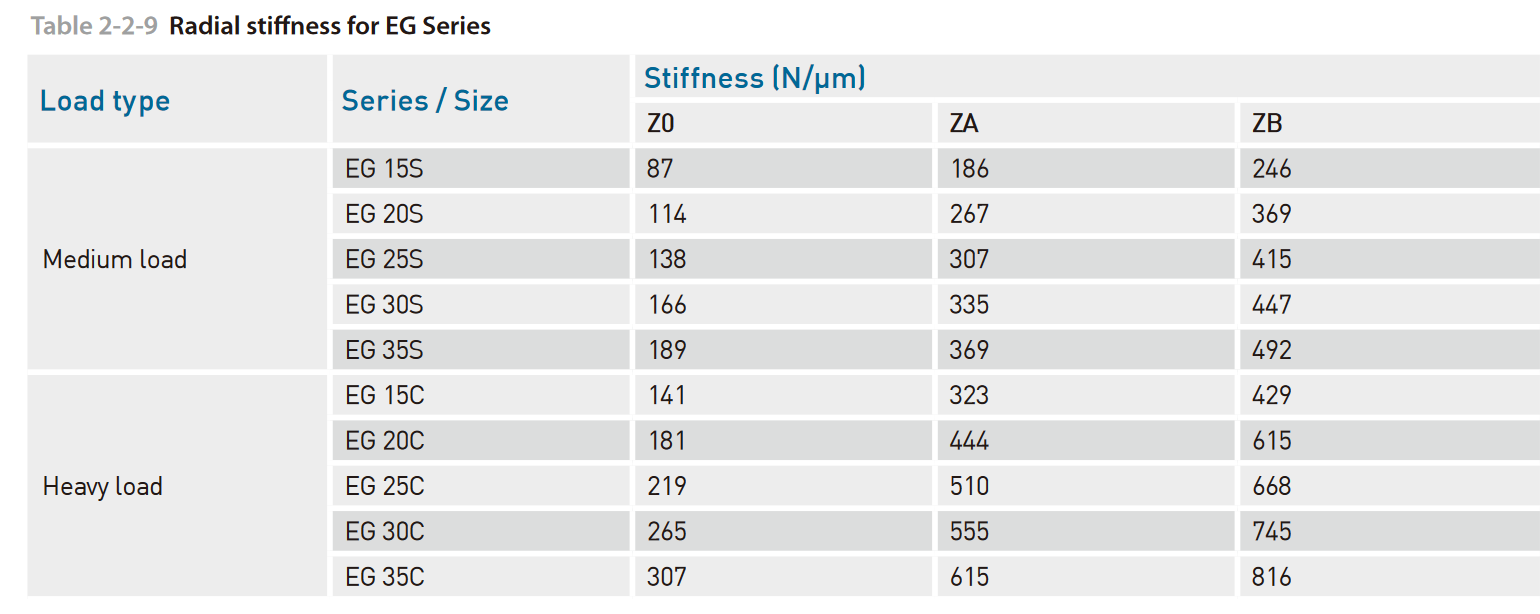
We can see that these are pretty impressive, the largest of which (with the highest preload) loading up to 800N (or 180 pounds of force) before moving even one micron.
Belts also have a stiffness rating, this paper discusses in fine detail the stiffness of GT2 belts, and we can get an idea of scaling here:
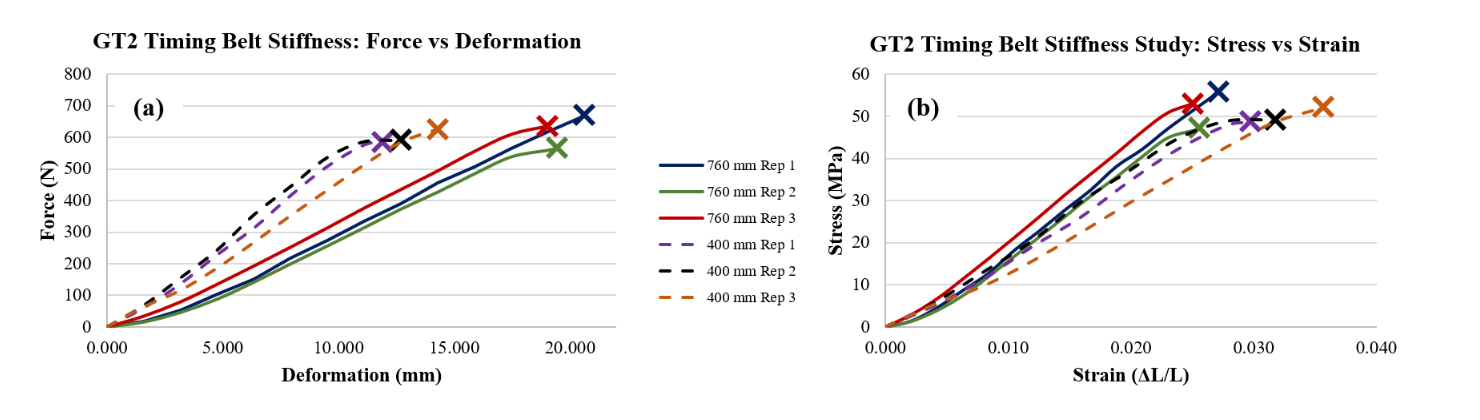
There’s also a gates document on belt tensile properties
Just picking the 400mm length of GT2 belt above, we see it deflects about 10mm under 500N of load (just before it breaks), so we have ~ 0.05 N / um of stiffness. On the other hand, even our smallest COTS linear guide above has 87 N / um of stiffness, for about three orders of magnitude difference. These are the kinds of ‘ball-parking’ exercises you can do during early design phases to pick winners.
Structural Loop
The stiffness of an entire machine is made up of many components. Typically, we are interested in i.e. how much a cutting head deflects with respect to the piece of stock it is meant to cut, in that case a “structural loop” - or the machine’s complete load path - looks something like this:
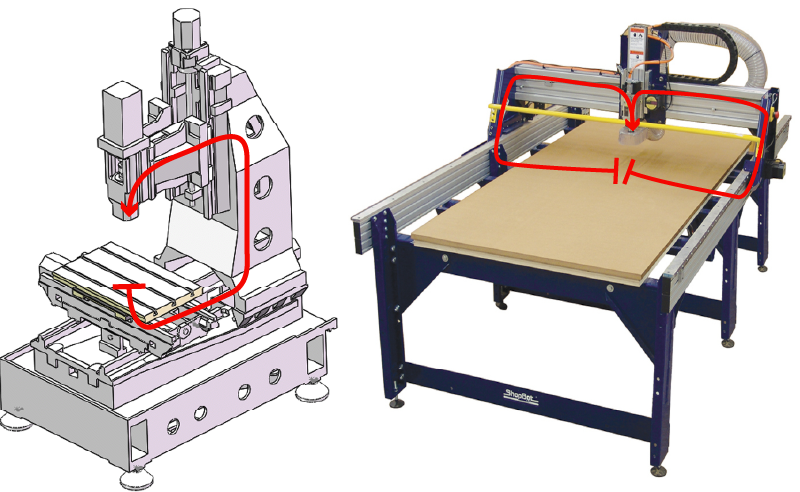
- loops include structural elements in the machine
- loops also include all drives, transmissions, and motors
Chatter vs. Static Deflection
We want stiffness in our machines first because it means our positioning stages will be more accurate: if we command a motor to some position, but our machine is under load (gravity, some cutting force, etc), we will miss our target position by whatever the machine’s deflection at that force is. For example given the belt example above, with only 50N of cutting force our machine will miss by one whole millimeter (this is also why we are excited about i.e. linear encoders mounted directly on-axis).
But the real reason we want to bring stiffness into (especially) milling machines is due to resonant chatter that often arise inside of the 1-15kHz frequencies. The stiffer our structure is, the farther outside of this regime we can send our machine’s resonant frequency.
Chatter is the enemy of the ‘lightweight milling machine’ dream. Many of us have dreamed of some kind of active chatter-cancellation circuitry, and I would encourage something like this as a class project.
Backlash
“Backlash” is best described as the ‘dead zone’ between positive and negative control inputs. From wiki:
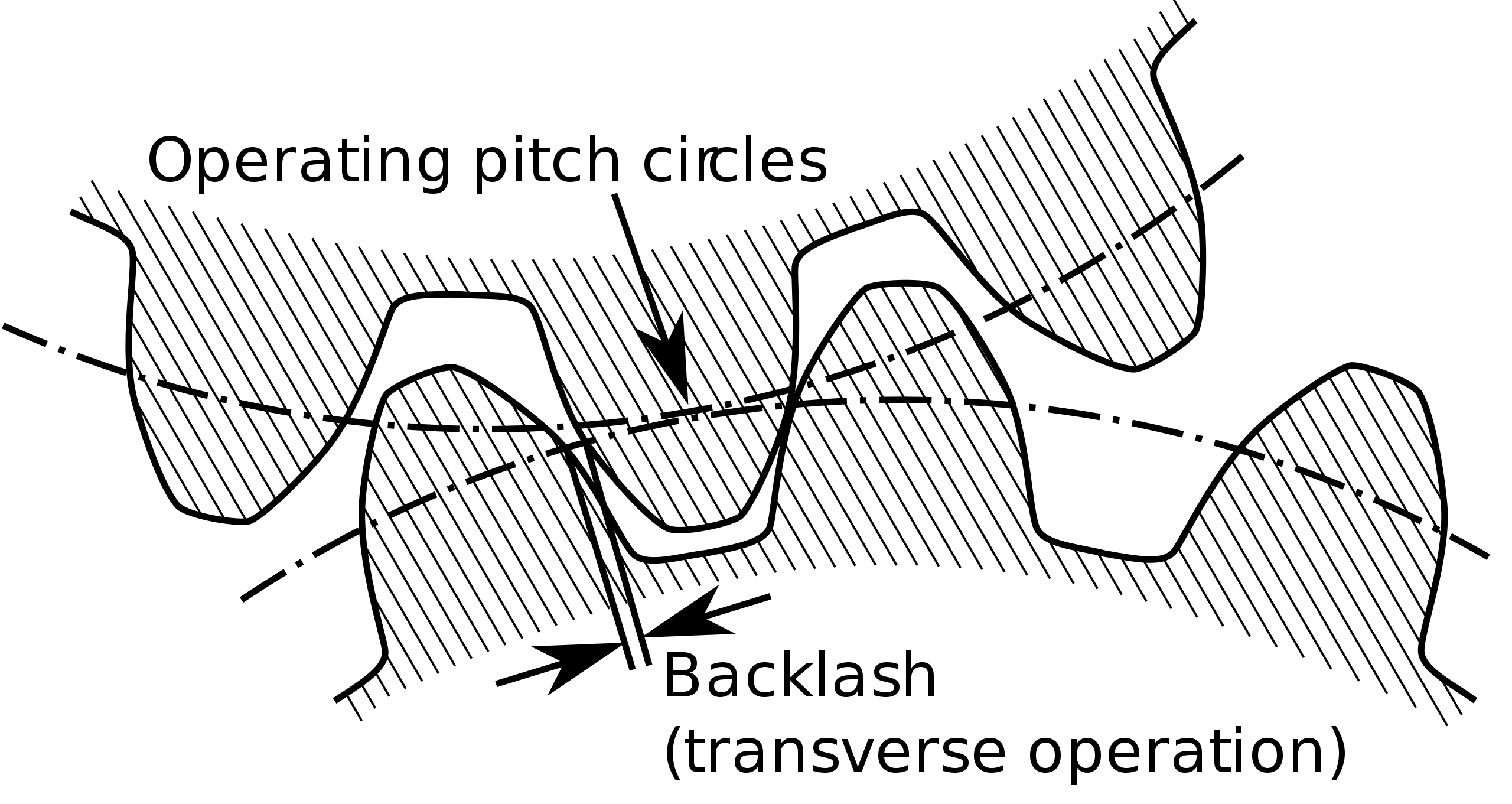
Another way to think of backlash is as having zero stiffness around the origin.
This ‘dead zone’ can exist anywhere between our actuator and our desired motion so that a plot of our mechanism’s output looks like this:
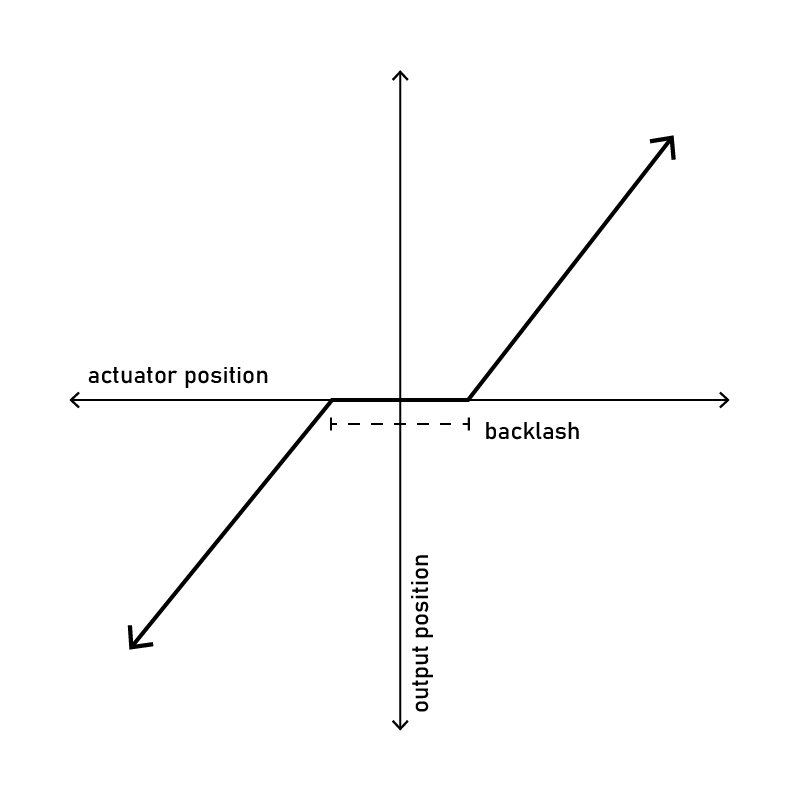
Backlash is an obvious result of poorly manufactured gear teeth, as drawn in the first figure here. However, it exists in almost all transmissions: leadscrews, belt drives, rack-and-pinions, etc.
Backlash also exists in motion guides (linear and rotary bearings) and can (and often does) exist in structures. Basically, backlash is ‘looseness’ (aka “play”) and wherever we can, we want our machines to feel ‘tight’ - if motors are powered on and holding torque, we should not be able to ‘wiggle’ anything about before meeting the motor’s output, or finding stiffness (resistance to wiggling) in the machine. Any ‘jiggle’ or ‘knocking’ we can find when we try to move a machine’s output around is backlash, and it’s very hard to control for (since it’s non-linear) - the best place to eliminate it is with good mechanical design.
Preload
If we leave something too loose we find backlash, but if we over-tighten we find friction. This is why most gearboxes have some amount of backlash: ensuring positive clearance minimizes friction. There’s a kind of zero-thickness ‘zero clearance’ zone between backlash and preload:
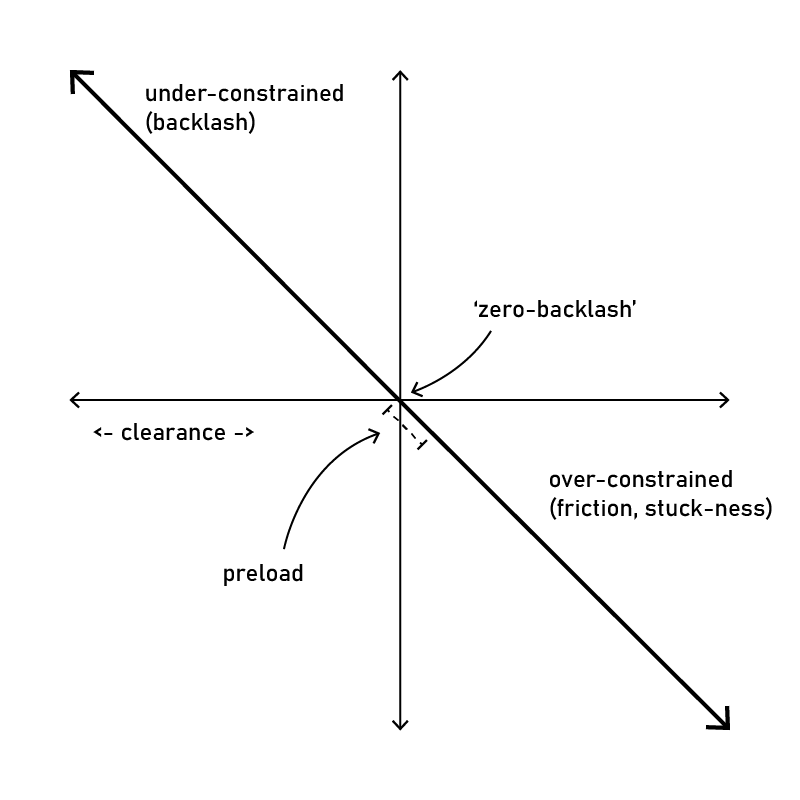
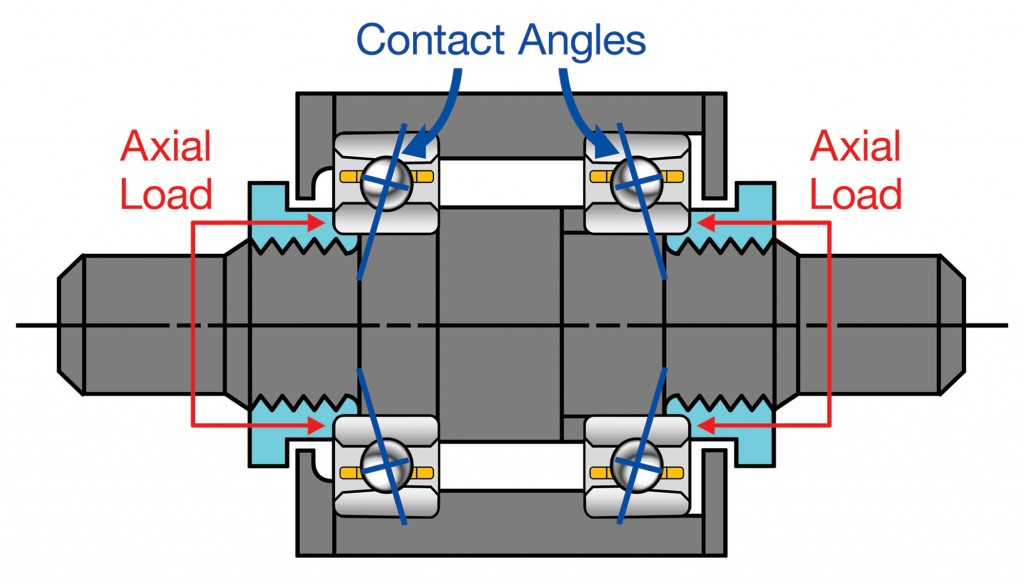
Consider these bearings:
Preloading is the art of building some positive clearance (as in, some ensured contact) between machine elements. In a way, we can even think of tightening bolts in a structure as preload: we are tensioning some spring force into a fastener to ensure that elements of our structure are constantly loaded into one another. Recall that our bolts are not innocuous hunks of threaded metal: their lengths make up a very stiff spring: when we torque a bolt to spec, we are really tensioning the bolt-as-a-spring to some preload spec.
The same kind of concept can apply to motion elements, i.e. how these bearings are tensioned into one another so as to ensure that the balls and races are in constant, deterministic contact:
The same principle can apply in linear guides, lead screws, etc.
Friction
I can’t talk about preload without reminding us of friction: positive preload always engenders friction: as we increase the normal force between elements (loading them against one another) we decrease their likelihood of slipping past one another.
So, why not perfect preload / zero backlash all the time? Exactly because perfect precision does not exist: if we add even 1/1000 of one mm of clearance, we have backlash, but if we add 1/1000 of one mm of contact, we have preload. Extremely well engineered applications exist where clearances approach a perfect zero, but here even changes to a component’s temperature affect it’s size, thus changing clearances. This is why extremely advanced equipment goes to the length of temperature controlling all axis and drive systems:
Alignment
Now that we’re through the stiffness triplet (stiffness, backlash and preload), we can talk about some machine layout principles.
First up is alignment: this is relatively straightforward: whenever possible, we want loads to align with forces.
Abbe Error
aka cosine error
Abbe Error is the simple note that angular error is amplified by distance - if we point a very long stick with a very small angular error, our final error (at the tip of the stick) can still be large.
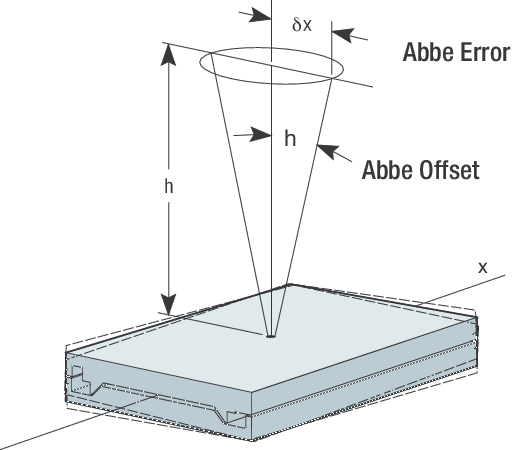
Abbe error and misalignment often show up together, or, when we minimize misalignment we are also likely to be minimizing abbe errors.

However, the trouble with laying elements right on top of eachother so as to be perfecty aligned is that they interfere. We cannot put the X axis directly through the workpiece, for example. So we will typically find that machines with large build volumes have larger “misalignments” between the work being done and the drives doing the work, i.e. in the shopbot above. In machines with typically small build volumes (as a fraction of total machine size) we will find that load-to-drive-offsets are small (again relative total machine size).
F = MA
This is just to say that mass relates to our ability to accelerate. This is why you will find many machine designers in the wild with fetishes for lightweight-ness. It is often worth the effort, especially for the ‘final stage’ of flying mass: the tool head.
Consider also that minimizing mass is also likely to minimize stiffness. We can be fast and stiff and heavy if we also spend thousands of dollars on high power drives and use tens of kW of energy.
Flatness, Straightness
It’s worth noting that nothing is truly flat and (given no other inputs) a linear axis can only be as accurate as the structure it runs on.
- cheap to reference, expensive to machine
- lugs
Adjustment
When you’re designing a machine, it’s worth planning ahead for adjustment. Most of the subtleties in machine design involve building small mechanisms for adjustment into larger assembles. These can include:
- belt tensioning (a kind of length adjustment)
- tramming (angular adjustments on linear axis)
- levelling (i.e. printer beds are rarely “simply secured” to a machine)
Many adustments can be achieved with simple slots, otherwise aided with set-screws or other threaded adjustment mechanisms.
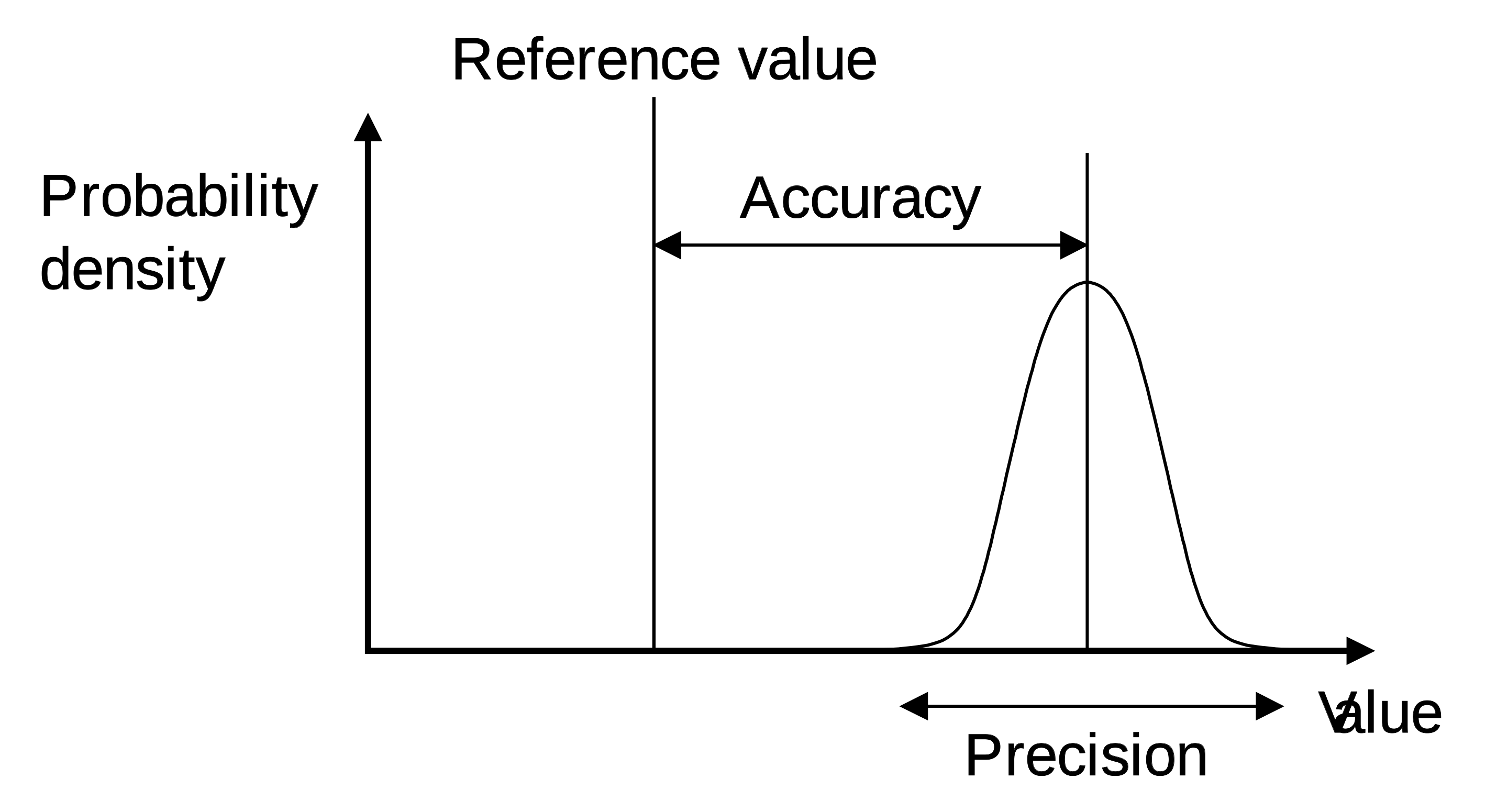
Precision vs. Accuracy
These are not the same thing: precision is our ability to reliably target the same space in a repeatable manner (aka: repeatability), and accuracy is our ability to hit an exactly addressed location in real space.
I.E. if, when I tell my X Axis to position at 100mm, it winds up at 101mm every time it is extremely precise, but not very accurate. If instead it targets somewhere between 100.1mm and 99.9mm every time, it is less precise but more accurate.
We can also discuss “resolution” - this refers to the size of the individually addressable locations in a machine. For example, if my same machine can only target either 100mm or 101mm, it has a 1mm resolution: not very great, even if we can hit that 100mm repeatably. We often see machine performance specified in terms of resolution because it’s very achievable with digital controls. Converting resolution into real accuracy and repeatability is another thing, and typically requires good mechanical design.