Laser box
My first pressfit furnature project was a box to keep our Epilog laser on top of. The design requirements were rigidity and capability of holding a lot of weight but not requiring a single screw except to attach hinges for the openable front panel, as things can be stored inside.
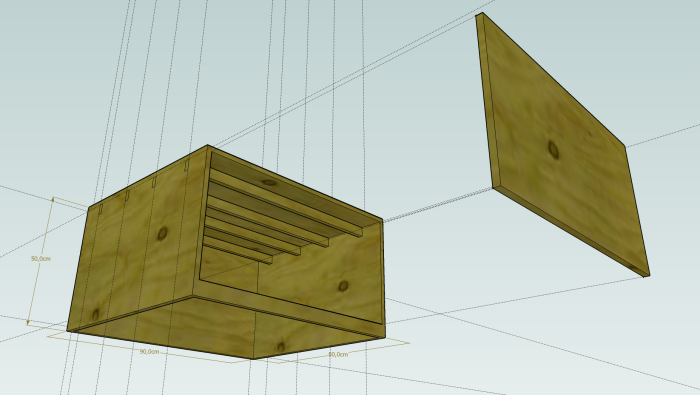
I did a rough sketch of the Laser box in Google Sketchup before laying out the individual pieces to be cut in the Shopbot command language.
Here we see the front of the assembled box. I carved our logo into the front of it, but the hinges still haven't been attached.
Here is a view of the side of the box. The teeth alternate to provide a lot of surface area to increase the strength of the pressfit lock. Hard to see on this image are the crossbars.
Here is a view inside. The crossbars are clearly visisble; they run from side to side and strengthen the top panel. They are all connected to the top panel by a set of bumps that slide into holes on the top panel.
Design files:
Computer Table
Time for something more ambitious. We needed a table for design computers and the CAMM, so I set about designing a table for it. Again, the no-screw policy was in place, and the table needed to be able to handle being banged about a lot.
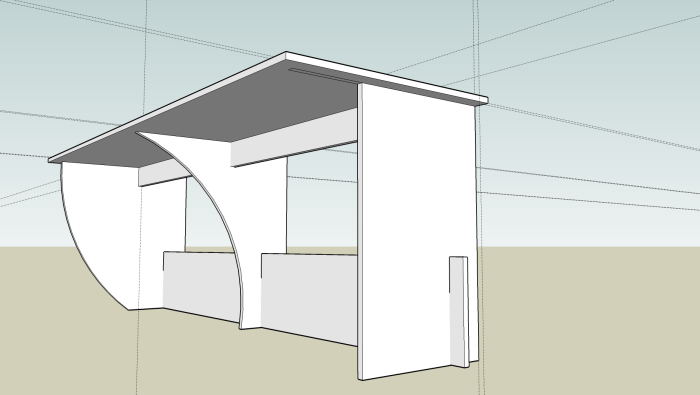
The sketchup drawing was originally stylized a bit with curvy legs. These turned out to be too wobbly so the outside legs were exchanged for square legs while the middle leg's curve was inverted to allow maneuvering chairs between the stations.

Here we can see how the legs fit through the top panel. In retrospect they shouldn't have gone all the way through as the minuscule gap will collect dirt.

The intersection between the leg, top plate and strengthening crossbar.

Intersection between bottom-bar that keeps the legs correctly spaced and the right leg.

The center leg with it's fancy curvature.

And the final assembly in use.
Design files:
- Sketchup file
- Partworks carve file 1
- Partworks carve file 2
- Shopbot part 1
- Shopbot part 2 (with old legs)
- New Legs
FabHouse
In Vestmannaeyjar we have an annual festival in the beginning of August where a substantial portion of the island's population move into white tents in a small valley and the population of the island tripples for a four day weekend. The white tents have stayed more or less the same since the 1890's, but the festival has been held every year since 1874. Here are pictures of the tents from the two festivals showing context and detail:


The design is very simple but could do with significant improvement. One issue is that it typically rains a lot at the festival and the wind sometimes gets very strong, even so much as to blow the tents away.
Taking the Hexayurt design, which is a very simple shelter design which is essentially an approximation of a geodesic dome made out of 4x8's, I ventured to create a pressfit version of the same for the last festival. I didn't manage to complete building it, but the designs are more or less ready.
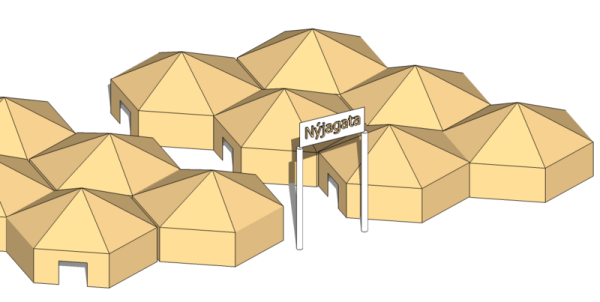
The sides of the house are made from six 4x8 sheets and have 13 cuts each. On the left side, four slots, 6" high each, on the right, five cuts makes for four locks that go into the slots. This is enough to make a hexagon of six 4x8s.
On the top of each side there are four slots, 18" each, which serve as receptacles for the roof pieces.
The roof is constructed from six 4x8 sheets. To start off you need to cut along the diagonal a jigsaw-like shape. In cutting this, you may leave out 4" from the middle, as this is the amount by which the sides shortened, minus 2" that we'll use later. At the shortest end of the two triangles you now have, you cut tabs that fit into the receptacle slots on the sides.
Finally, on the longer of the two shorter ends of the triangles, you cut alternating dovetails, 1" deep. These dovetails serve to merge the ends together so that the roof is rigid.
Now, patch the jigsaw bits together and apply some adhesive. Next, lower the roof pieces one by one into place, fitting them to each other on the dovetail edges.
Chimney edition: When preparing the triangles, leave a 2.5" long cut off the corner end of each one where the longer short end meets the hypotenuse, and make the flat end into half of a 0.5" deep tab. Then, when you assemble the roof, you'll have six 0.5" tabs jutting out into a hole in the roof. Now, make three 6" long boards and three 8" long boards that fit the gap, each with a slot near the bottom for the tab, and construct a hexagon chimney.
Before assembling, cut locking tabs into the three 8" boards. Now make a 8" diameter hexagon with slots for the locking tabs that can be placed on top of the chimney, to stop rain from entering. That way you have three 1.75" holes on the top to let smoke out.
Please consider that for cooking fires you might want to make the chimney out of inflammable materials and lengthen the chimney to reach down to the fire.
Design files:
Thoughts on pressfits and geometry
Although I couldn't do the GIK assembly kit, I did a bit of thinking about alternative geometries. One thought that came up after seeing Johann's Hoberman sphere was it's relationship with the Banach-Tarsky paradox in geometry, which states that a ball can be decomposed into a finite number of point sets and reassembled into two balls identical to the first one. Of course, in physical reality this is somewhat harder to do, but using the Hoberman sphere we could approximate the effect to a convincing extent. Consider this a thought experiment.

Consider one were to build a Hoberman sphere on a molecular scale, where each piece is less than 50 atoms, assume covalent connections internally for strength/rigidity and hydrogen bonds between pieces. Compile enough of them to build a sphere that has the dimension to be anything from the size of a golf ball to the size of a beach ball, but because it's built of molecular-scale pieces you can weave it really tight so that in either case it appears not to have any holes, although it may be translucent when beach-ball sized. (assume it only takes a couple hundred Newtons of force to alter the dimension, although the reality may be different.)
Now let's scale it down to golf-ball size, maximizing the density of the Hoberman sphere. Now take a photograph and then disassemble the pieces and use them to build two new Hoberman spheres, but these consist of far fewer parts and will therefore not be able to scale up to beach-ball size, but may be able to scale up to and beyond the golfball size.
If you see where I'm going with this, consider the thought experiment over. Of course, this isn't really the Banach-Tarsky paradox in play, but to anybody not familiar with Hoberman spheres it might look like it.