Gradient Formulation
Taking the strain energy minimization problem, it can be seen that the objective function depends on the gradient of the displacements, which are found by inverting the stiffness matrix. Instead, taking the derivative of the F = Ku equation with respect to the design variables d allows us to formulate the gradient of the displacements in terms of the gradient of the stiffness matrix, not its inverse. Since we explicitly know the dependence of the stiffness matrix on the design variables, this can be determined analytically.

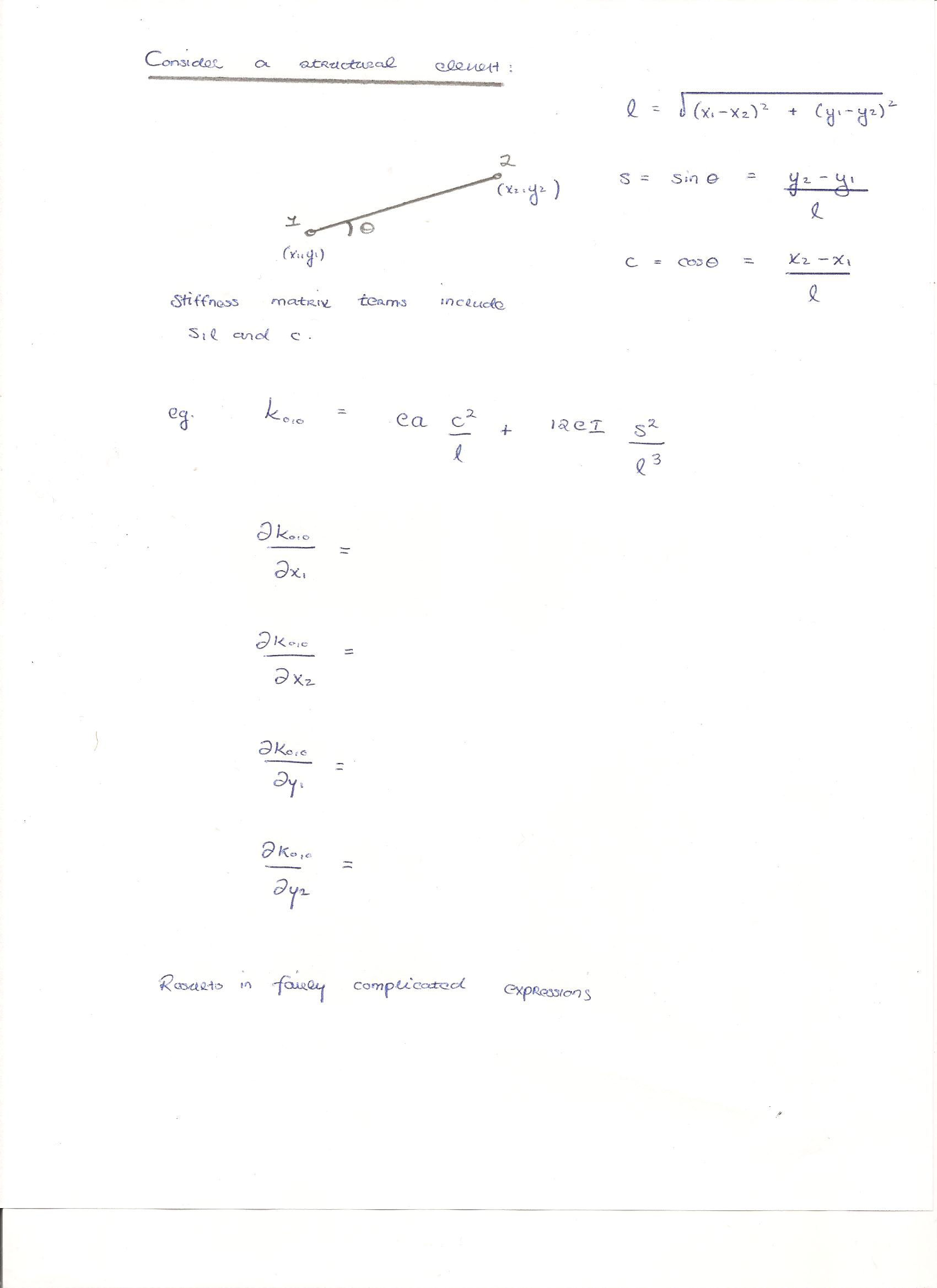
This is a somewhat messy calculation. Consider the handwritten text below, which shows the dependence of a single term in the local stiffness matrix on the x and y components of the nodal coordinates. For practical purposes, these would need to be evaluated using a symbolic math environment. Note, however, that the stiffness matrix depends linearly on the element size variables a and I. Formulating the gradient of sizing problems is therefore straightforward.