Finite Differences: Partial Differential Equations
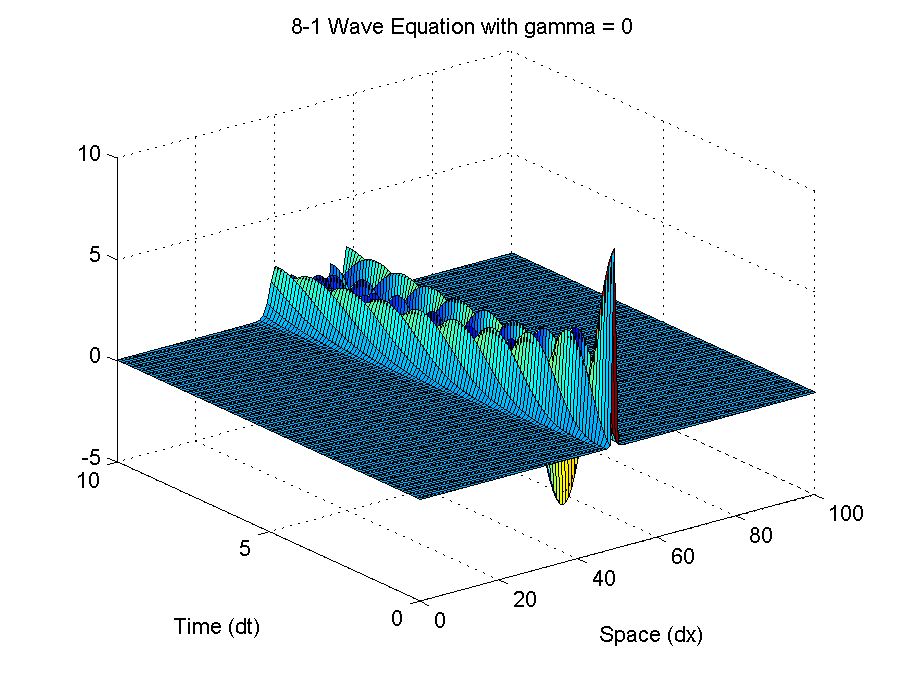
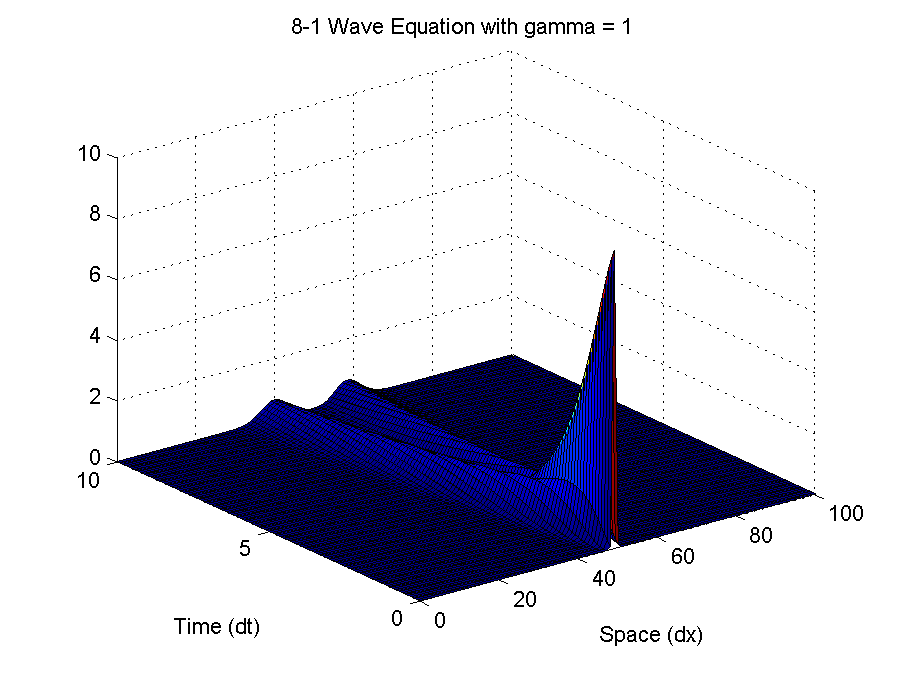 It can be seen that numerical dissipation due to the extra fictitious damping term makes the solution to Part (h) much smoother than Part (f).
It can be seen that numerical dissipation due to the extra fictitious damping term makes the solution to Part (h) much smoother than Part (f).
%% Meng Yee CHUAH % Week 5 - Finite Differences: Partial Differential Equations %% 8.1 close all; clear all; clc; % Parameters dt = 1e-1; dx = 1e0; v = 1; % v <= dx/dt for stability xfinal = 100; x = 0:dx:xfinal; nx = length(x); tfinal = 10; t = 0:dt:tfinal; nt = length(t); gamma = 0; % Difference between parts (f) and (h) u = zeros(3,nx); % [u(n-1); u(n); u(n+1)] u(:,floor(nx/2)) = 10*ones(3,1); U = zeros(nt,nx); for n = 1:nt % Time for j = 2:nx-1 % Space u1 = u(2,j+1)-2*u(2,j)+u(2,j-1); u0 = u(1,j+1)-2*u(1,j)+u(1,j-1); u(3,j) = ((v*dt/dx)^2)*u1+2*u(2,j)-u(1,j)+ ... (gamma*dt/(dx^2))*(u1-u0); end u(1,:) = u(2,:); u(2,:) = u(3,:); U(n,:) = u(3,:); end figure('Units','inches','Position',[0 0 6 4.5],'PaperPosition',[0 0 6 4.5]); surf(x,t,U); h = title(sprintf('8-1 Wave Equation with gamma = %g',gamma)); % set(h,'Interpreter','latex'); xlabel('Space (dx)'); ylabel('Time (dt)'); saveas(gcf,sprintf('8-1 Wave Equation with gamma = %g.png',gamma)); saveas(gcf,sprintf('8-1 Wave Equation with gamma = %g.fig',gamma));
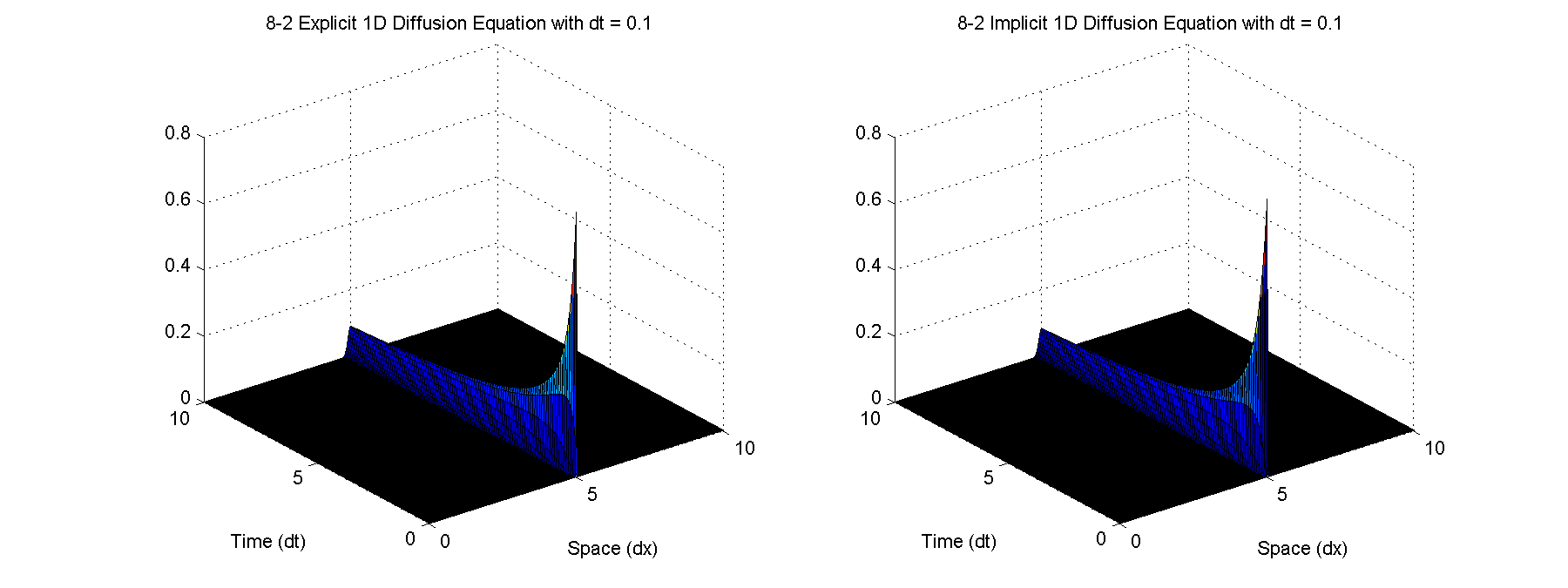
 For dt = 0.1, both implicit and explicit methods converge well.
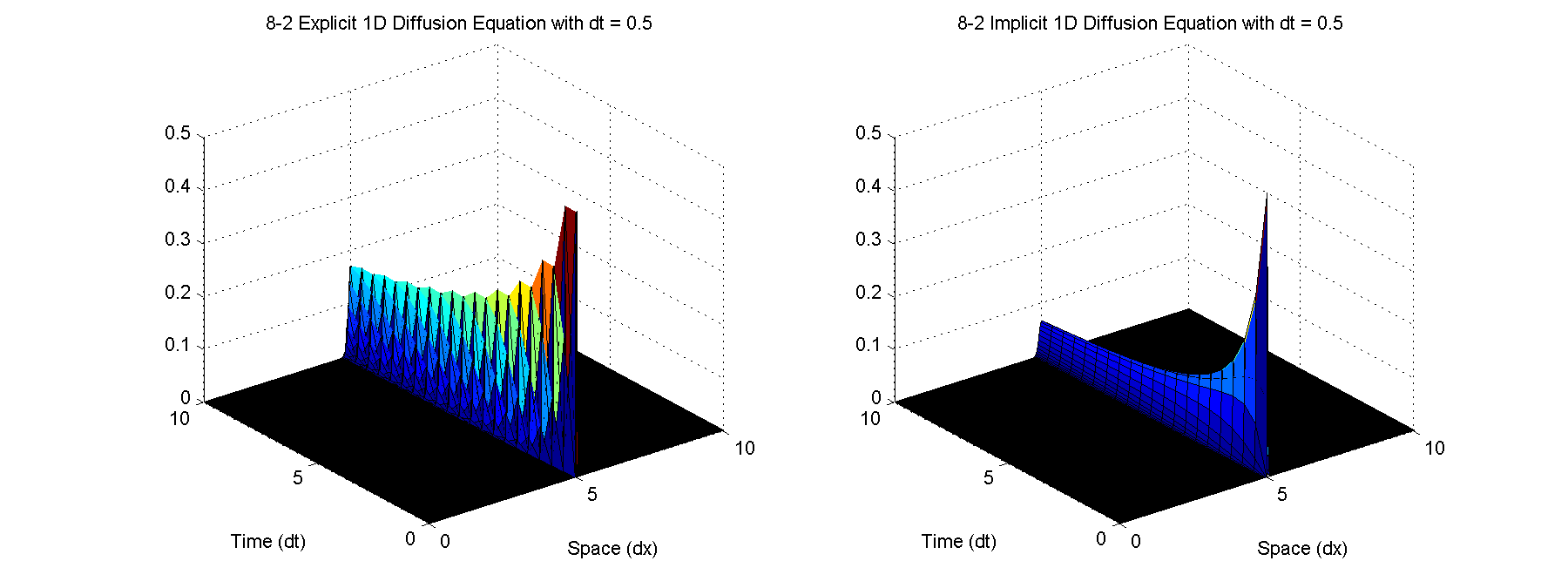
For dt = 0.1, both implicit and explicit methods converge well.For dt = 0.5, the explicit method converges but with much oscillation while the implicit method does not have this problem.
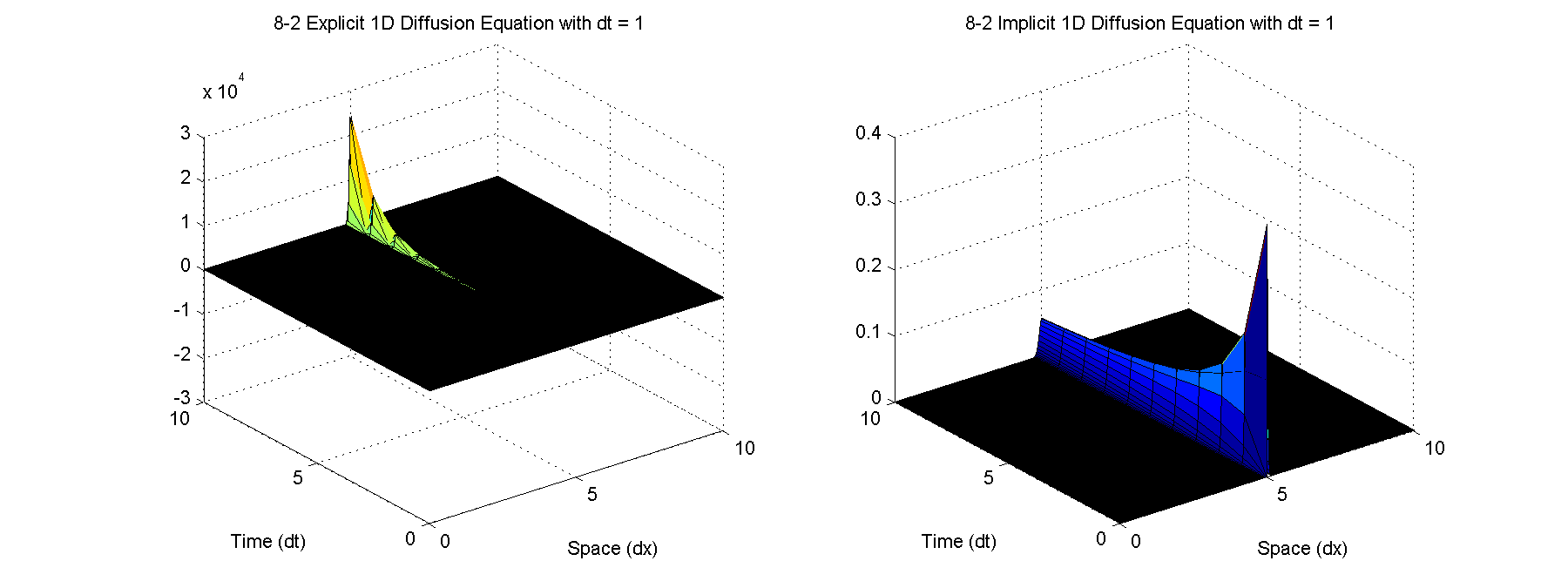
For dt = 1, the explicit method diverges due to instability by violating the Courant condition while the implicit method still converges without any problems.
%% 8.2 close all; clear all; clc; % Parameters D = 1; dx = 1; nx = 500; xfinal = 10; x = linspace(0,xfinal,nx); tfinal = 10; for dt = [0.1 0.5 1] t = 0:dt:tfinal; nt = length(t); alpha = D*dt/(dx^2); uexp = zeros(3,nx); % [u(n-1); u(n); u(n+1)] uexp(:,floor(nx/2)) = 1*ones(3,1); Uexp = zeros(nt,nx); uimp = zeros(3,nx); % [u(n-1); u(n); u(n+1)] uimp(:,floor(nx/2)) = 1*ones(3,1); Uimp = zeros(nt,nx); % Tridiagonal matrix a = -alpha*ones(1,nx); b = (1+2*alpha)*ones(1,nx); c = -alpha*ones(1,nx); a(1) = 0; a(nx) = 0; b(1) = 1; b(nx) = 1; c(1) = 0; c(nx) = 0; cp = zeros(1,nx); dp = zeros(1,nx); cp(1) = c(1)/b(1); dp(1) = uimp(2,1)/b(1); for n = 1:nt % Explicit (8.20) for j = 2:nx-1 uexp(3,j) = uexp(2,j)+alpha*(uexp(2,j+1)-2*uexp(2,j)+uexp(2,j-1)); end uexp(2,:) = uexp(3,:); Uexp(n,:) = uexp(3,:); % Implicit (8.25) % Gauss elimination forward pass for i = 2:nx-1 cp(i) = c(i)/(b(i)-a(i)*cp(i-1)); dp(i) = (uimp(2,i)-a(i)*dp(i-1))/(b(i)-a(i)*cp(i-1)); end % Reverse pass uimp(2,nx) = dp(nx); for i = nx-1:-1:2 uimp(2,i) = dp(i)-cp(i)*uimp(2,i+1); end Uimp(n,:) = dp; end figure('Units','inches','Position',[0 0 6*2 4.5],'PaperPosition',[0 0 6*2 4.5]); subplot(1,2,1); surf(x,t,Uexp); title(sprintf('8-2 Explicit 1D Diffusion Equation with dt = %g',dt)); xlabel('Space (dx)'); ylabel('Time (dt)'); subplot(1,2,2); surf(x,t,Uimp); if dt == 0.1 zlim([0 0.8]); end if dt == 0.5 zlim([0 0.5]); end title(sprintf('8-2 Implicit 1D Diffusion Equation with dt = %g',dt)); xlabel('Space (dx)'); ylabel('Time (dt)'); saveas(gcf,sprintf('8-2 1D Diffusion Equation with dt = %g.png',dt)); saveas(gcf,sprintf('8-2 1D Diffusion Equation with dt = %g.fig',dt)); end