James Pelletier
MAS.864 Nature of Mathematical Modeling
Optimization
This week I enjoyed a great first experience with NumPy. The two things that caused me trouble at first were linking versus copying arrays (i.e., I was overwriting arrays when I thought I was editing copies) and data types (i.e., multiplying by 1/2 was different than multiplying by 0.5 because I did not declare the float data type when I initialized the array). I now prefer NumPy to MATLAB in terms of plotting, and I am becoming more familiar with the matrix manipulations in NumPy.
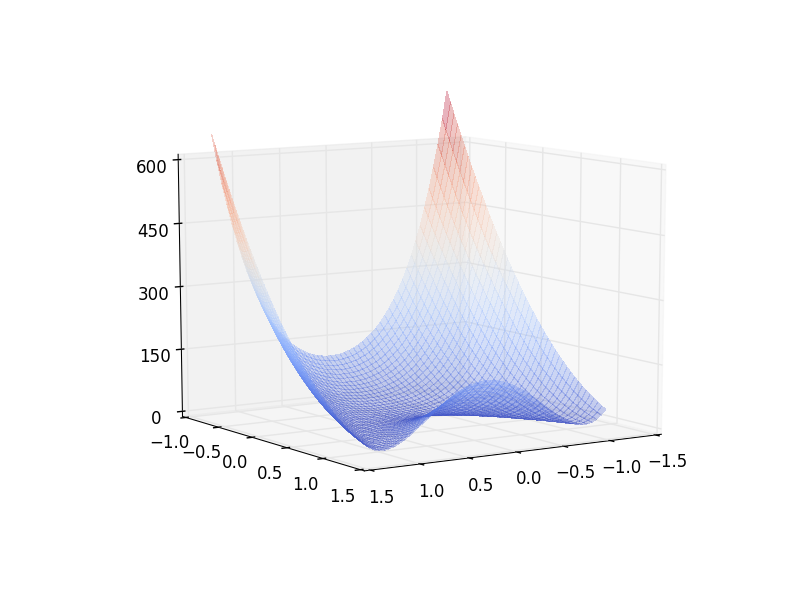
(14.1a) We first plot the Rosenbrock function $$f = (1 - x)^2 + 100 \left( y - x^2 \right)^2$$.
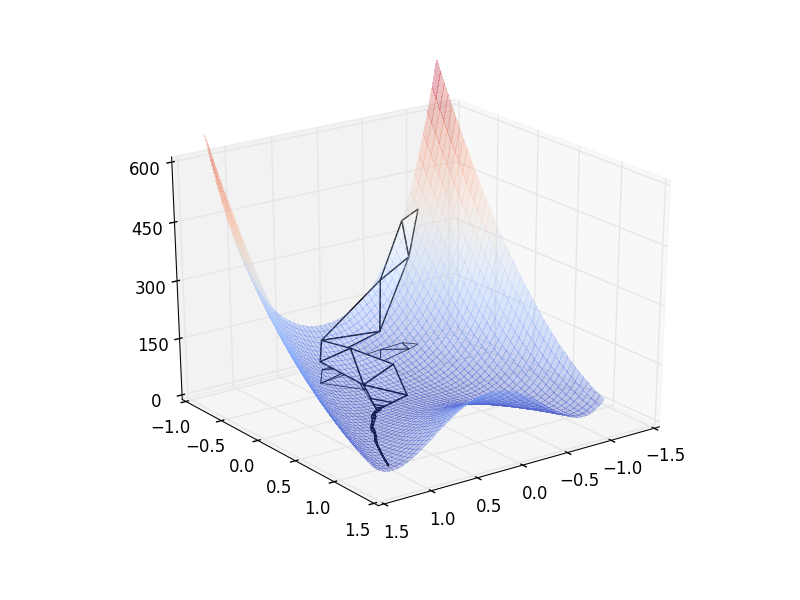
(14.1b) Downhill simplex: We stopped the algorithm when the simplex area fell below a minimum threshold (in this case, 0.00001). The algorithm found the minimum at $[1.01, 1.02]$, within 0.02 of the true minimum at $[1, 1]$; and the minimum value at $9.4 \times 10^{-5}$, within $1 \times 10^{-4}$ of the true minimum value at 0. The algorithm evaluated the Rosenbrock function 105 times. The code is here txt, py.
(14.1c) Direction set: We tried to stop the algorithm when the total displacement per iteration through both basis functions fell below a minimum threshold; however, the algorithm did not converge, so we fixed the number of iterations to 80 loops. The algorithm found the minimum at $[0.97, 0.94]$, within 0.07 of the true minimum at $[1, 1]$; and the minimum value at $7.9 \times 10^{-4}$, within $1 \times 10^{-3}$ of the true minimum value at 0. The algorithm evaluated the Rosenbrock function 14706 times. The code is here txt, py.
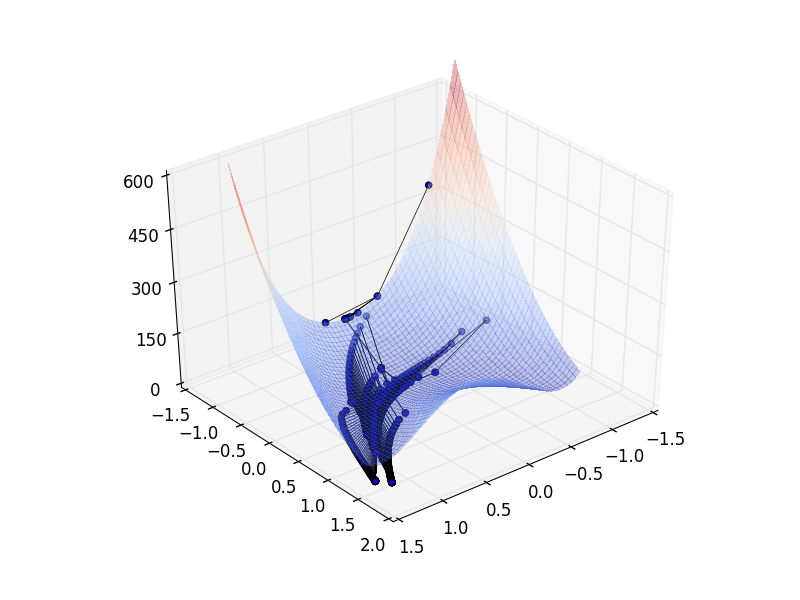
(14.1d) Conjugate gradient: We tried to stop the algorithm when the total displacement per iteration through both basis functions fell below a minimum threshold; however, the algorithm did not converge, so we fixed the number of iterations to 80 loops. The algorithm found the minimum at $[0.78, 0.61]$, within 0.45 of the true minimum at $[1, 1]$; and the minimum value at $0.046$, within $0.1$ of the true minimum value at 0. The algorithm evaluated the Rosenbrock function 5215 times. The code is here txt, py.
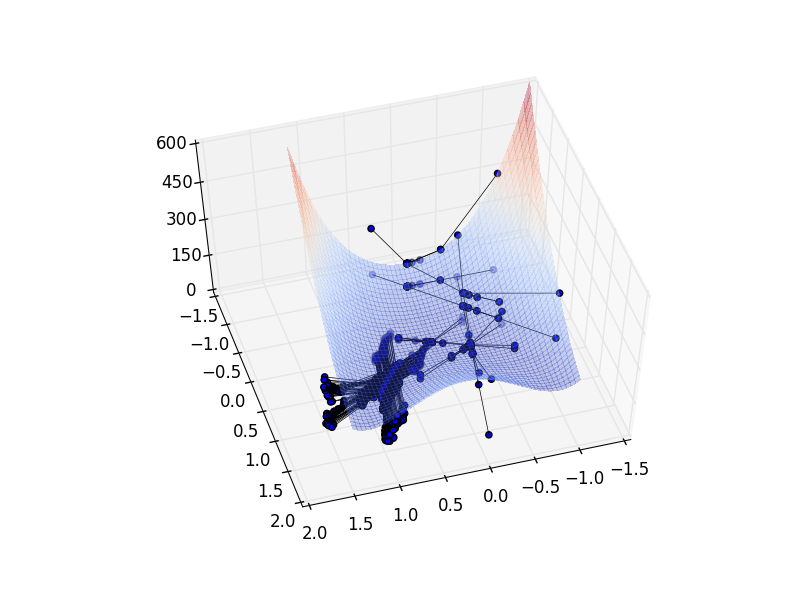
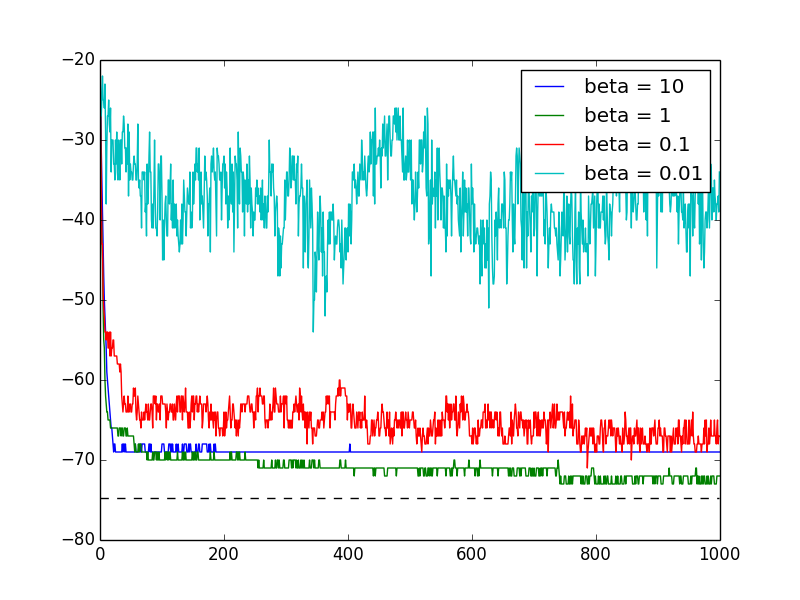
(14.2) Simulated annealing: The code is here txt, py.
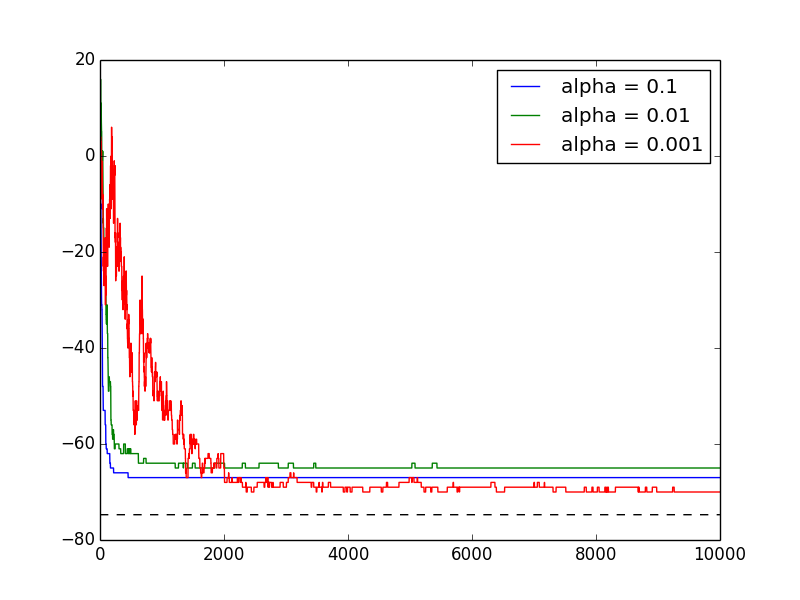
(14.3) Genetic algorithm: The code is here txt, py.