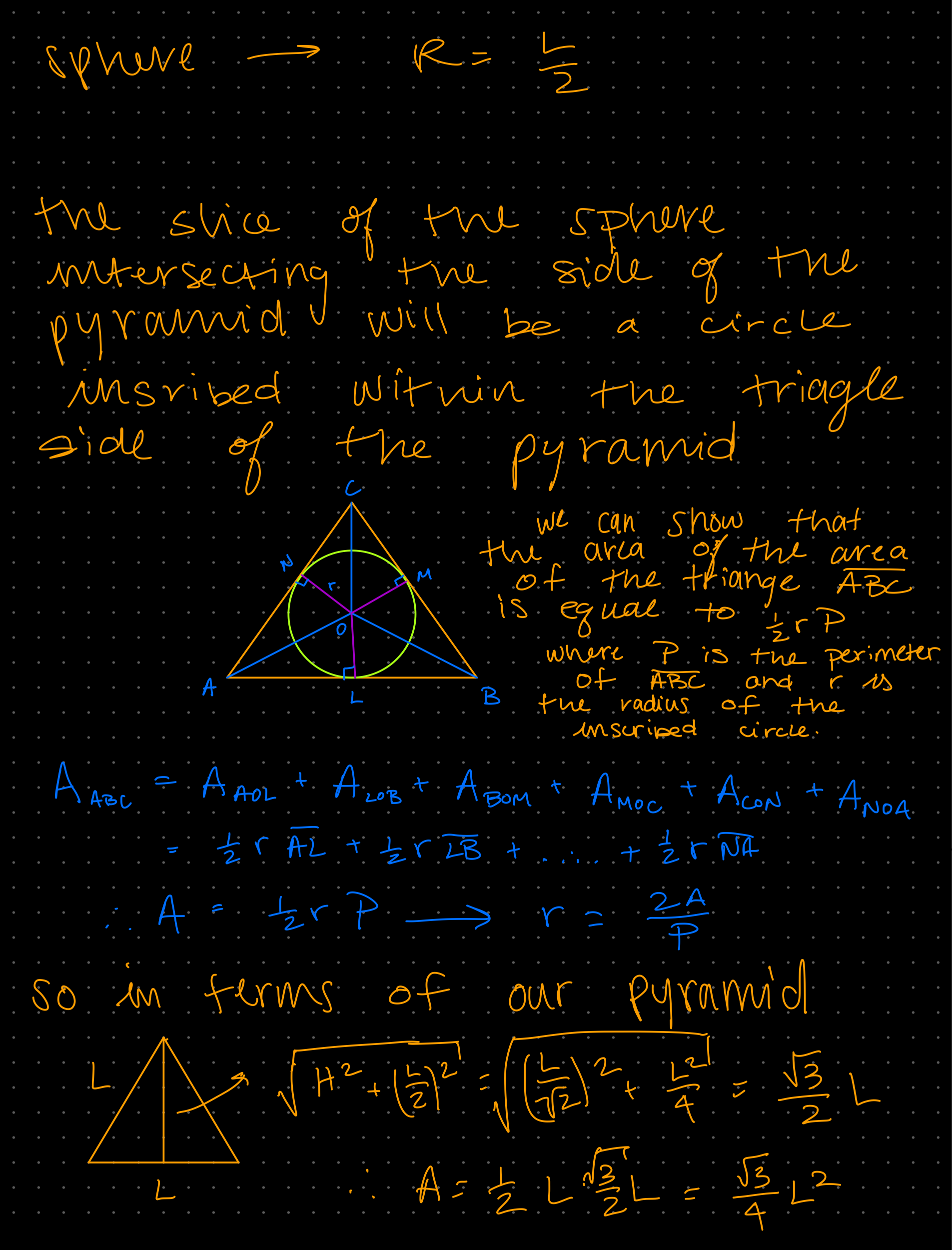
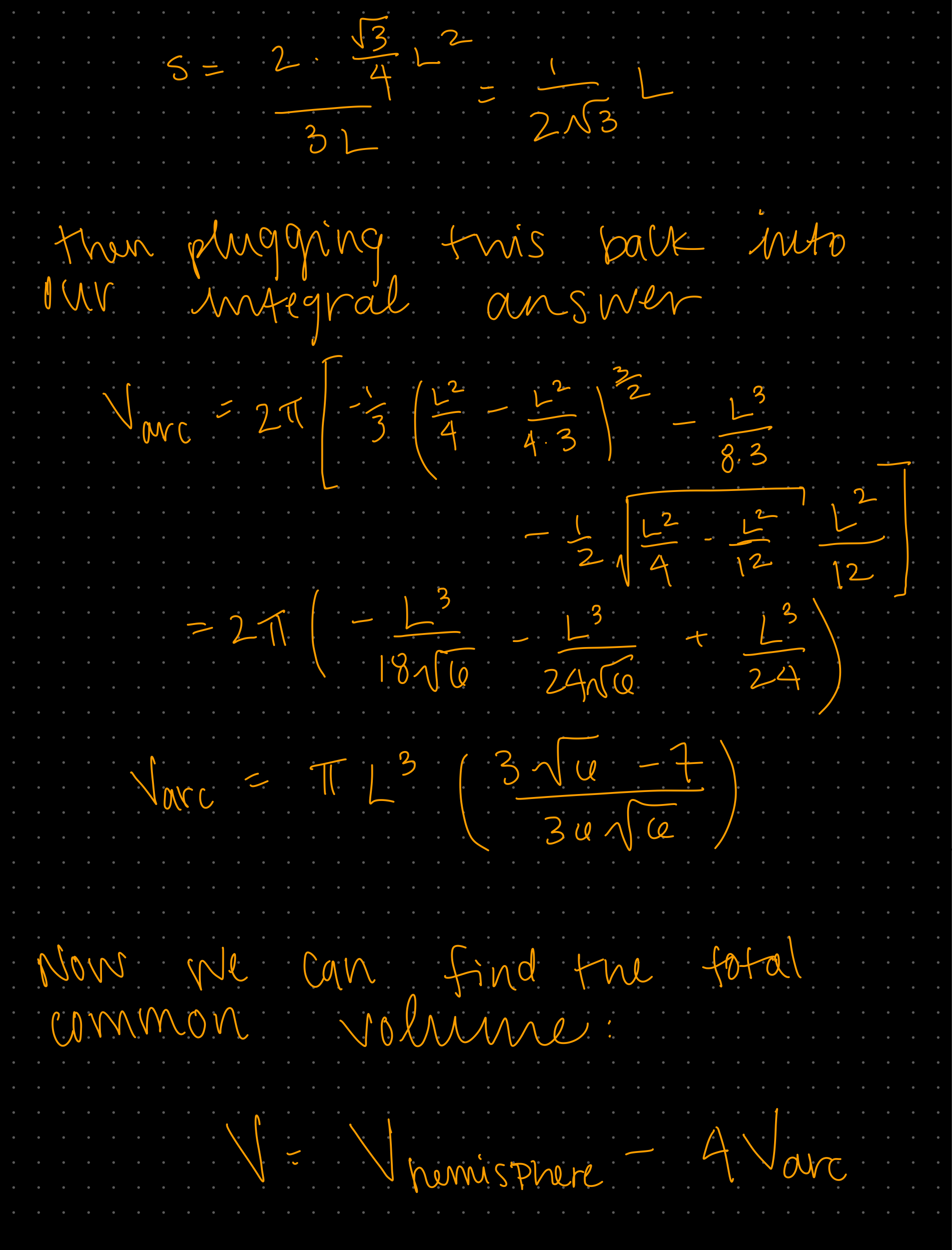Week 1

Problem Set

Feburary 10th

all problems from Chapter 2: Units and Magnitudes

Problem 1

(a) how many atoms are there in a yoctomole?

\[1 \text{ yoctomole} \left(\frac{1 \text{ mole}}{10^{24} \text{ yoctomoles}}\right)\left(\frac{6.022\times10^{23} \text{ atoms}}{1 \text{ mole}}\right) = 0.601 \approx 1 \text{ atoms}\]

(b) How many seconds in a nanocentury?

\[1 \text{ nanocentury}\left(\frac{1\text{ century}}{10^9 \text{ nanocentury}}\right)\left(\frac{100 \text{ years}}{1 \text{ century}}\right)\left(\frac{365 \text{ days}}{1\text{ year}}\right)\left(\frac{24\text{ hours}}{1\text{ day}}\right)\left(\frac{3600\text{ s}}{1\text{ hour}}\right) = 3.154 \text{s}\]

There are about \(\pi\) seconds in a nanocentury.

Problem 2

How tall would a stack of DVDs containing 1 exabyte of data be?

Most common DVDs (single sided and single layer) can store 4.7 GB of data and are 1.2mm thick (source).

\[1 \text{ exabyte} \left(\frac{10^{18}\text{ bytes}}{1 \text{ exabyte}}\right) \left(\frac{1 \text{ DVD}}{4.7\times 10^{9} \text{ GB}}\right) \left(\frac{1.2 \text{ mm}}{1 \text{ DVD}}\right) = 2.55 \times 10^5 \text{m}\]

The Von Karman line (distance from sea level to space) is 100 km = \(10^5\) m, so a stack of DVDs containing 1 exabyte of data would enter space.

Problem 3

What is the largest number that could be written if every atom in the universe were used to store 1 bit?

There are about \(10^{82}\) atoms in the universe (interesting derivation here). The largest possible number that could be written with \(10^82\) bits would have value 1 in each digit, which can be converted to base10 with the following summation

\[\sum^{10^{82}}_{n=0} 2^n \approx \int^{10^{82}}_{0} 2^n dn = \frac{2^{10^{82}}}{ln2} - \frac{1}{ln2} \approx 2^{10^{82}}\]

everything besides \(2^{10^{82}}\) is neglgible because it’s so big. converting this to base10

\[10^x = 2^{10^{82}} \\ x\cdot \log10 = 10^{82}\cdot\log2 \\ x = 3.01\times10^{81}\]

so the largest number that could be recorded (for one bit per atom) is

\[10^{3\times10^{81}}\]

Note : an easy thing to remember here is \(2^{10} \approx 10^3\).

Problem 4

Compare the gravitational acceleration due to the mass of the Earth at its surface to that produced by a 1 kg mass at a distance of 1 m and express the ratio in decibels.

Gravitational acceleration due to the mass of the earth at its surface is -9.8 m/s.

Gravitation acceleration of a 1 kg mass at a distance 1 m away from it is

\[g_{1} = -\frac{GM}{r^2} \hat r \\ g_1 = -\frac{(6.67\times10^{-11}\text{ N}\cdot\text{m}^2\cdot\text{kg}^{-1})(1 \text{ kg})}{(1\text{ m})^2} \\ g_1 = - 6.67\times 10^{-11} \text{m/s}^2\]

The ratio between these two gravitation accelerations is

\[20\log\left(\frac{9.8}{6.67\times 10^{-11}}\right) = 223.34 \text{ dB}\]

Problem 5

(a) estimate the amount of chemical energy in a ton of TNT.

Chemical reactions occur between molecules with \(\mathcal{O}(1\text{eV})\) bond energies. Assuming that TNT is made up entirely of nitrogen, which has an atomic weight of 14 amu, the chemical energy can be found with

\[1 \text{ ton TNT} \left(\frac{10^6\text{ g}}{1\text{ ton}}\right) \left(\frac{6.022\times10^{23} \text{ N atoms}}{14 \text{ g}}\right) \left(\frac{1 \text{ eV}}{1 \text{ N}}\right) \left(\frac{1.602\times10^{-19} \text{ J}}{1 \text{ eV}}\right) = 6.88\times10^{9} \text{ J}\]

(b) How much uranium would be needed to make a nuclear explosion equal to the energy in a chemical explosion of 10,000 tons of TNT?

10,000 tons of TNT has about \(10^{13}\) J of energy ( from \(10,000\cdot10^{9}\)).

Nuclear excitations are on the order of 1 MeV

\[10^{13} \text{ J} \left(\frac{1 \text{ eV}}{1.602\times10^{-19} \text{ J}}\right) \left(\frac{1 \text{ MeV}}{10^6 \text{ eV}}\right) = 6.2\times10^{26} \text{MeV}\]

Therefore, about \(6.2\times10^{26}\) uranium nucleons need to explode, i.e. undergo fission, and there are 238 nucleons in a single uranium atom.

\[\frac{6.2\times10^{26} \text{ nucleons}}{238 U} \left(\frac{238 \text{ g}}{6.022\times10^{23}\text{ U atoms}}\right) \rightarrow 104 \text{ g of U}\]

So 104 grams of uranium would need to explode, assuming 100% fission rate, which probably isn’t the case at all.

(c) Compare this to the rest mass energy of the amount of material

Rest mass energy is given by \(E=mc^2\), so

\[E = (0.104 \text{ kg})(3\times10^8 \text{ m/s})^2 = 9.37 \times 10^{18} \text{ J}\]

Problem 6

(a) What is the approximate de Broglie wavelength of a thrown baseball?

Assuming that the baseball is thrown in the MLB, the mass of the baseball is 146 g and the average pitch velocity is 95 mph (42.5 m/s). Therefore, the de Broglie wavelength is given by

\[\lambda = \frac{h}{mv} = \frac{6.626\times10^{-34} \text{ Js}}{0.145 \text{ kg}\cdot 42.5 \text{ m/s}} \\ \lambda = 1.08\times10^{-34} \text{ m}\]

(b) what is the de Broglie wavelength of a molecule of nitrogen gas at room temperature and pressure?

First, the mass of a molecule of nitrogen gas, N\(_2\) is

\[m_{N_2} = 28.02 \text{ amu} \left(\frac{1.66\times10^{-27}}{1}\right) = 4.65\times10^{-26} \text{ kg}\]

To find the velocity, we can use the equipartition theorem. Nitrogen gas has 5 degrees of freedom (3 translational and 2 rotational), therefore it’s potential energy is \(5/2k_bT\). Equating this to the kinetic energy of the moving molecule, we can find the velocity.

\[\frac{1}{2}mv^2 = \frac{5}{2}k_bT \\ v = \sqrt{\frac{5k_bT}{m}}\]

therefore, the de Broglie wavelength is

\[\lambda = \frac{h}{\sqrt{5k_bTm}} = 2.16\times10^{-11} \text{ m}\]

(c) What is the typical distance between the molecules in the gas? There is probably a more rigorous statistical mechanics derivation for this, but being lazy - I think it could be done with basic dimensional analysis …

We know the pressure and temperature of the molecules, and knowing that temperature is related to energy through Boltzman’s constant, we can look at the units of each variable and figure out how to arange them such that we find the volume a single molecule takes up

\[\frac{[\text{J}]}{[\text{Pa}]} = \frac{\text{kg}\cdot\text{m}^2}{\text{s}^2} \cdot \frac{\text{m}\cdot\text{s}^2}{\text{kg}} \\ \therefore V = \frac{k_bT}{P}\]

This volume is describing the space that a single nitrogen molecule would take up, so assuming it to be a sphere, we can find the distance between molecules, i.e. the radius of the sphere.

\[\frac{4}{3}\pi r^3 = \frac{k_bT}{P} \\ r^3 = \frac{3}{4\pi}\frac{k_bT}{P} \\ r = \sqrt[3]{\frac{3}{4\pi}\frac{1.38\times10^{-23}\text{ J/K}(293\text{ K})}{1.01\times10^5 \text{ Pa}}} \\ r = 2 \times 10^{-9} \text{ m}\]

(d) At what temperature does the wavelength become comparable to the distance between the molecules?

Rearange the final equation from part (c) to solve for \(T\) with \(r\) equal to the de Broglie wavelength.

\[T = \frac{4\pi}{3}r^3 \frac{P}{k_b} \\ T = \frac{4\pi}{3}(2\times10^{-11} \text{ m})^3 \frac{1.01\times10^5\text{ Pa}}{1.38\times10^{-23}\text{ J/K}} \\ T = 0.245 \text{ mK}\]

Problem 7

(a) What is the escape velocity required for a mass \(m\) at a distance \(r\) from another mass \(M\), given that the potential at \(m\) is \(-GMm/r\)?

For the mass to escape the potential, it’s kinetic energy must totally cancel out its potential energy

\[\frac{1}{2}mv^2 = \frac{GMm}{r} \\ v^2 = \frac{2GM}{r} \\ v = \sqrt{\frac{2GM}{r}}\]

(b) find the radius in which nothing can escape due to the limit of the speed of light.

solve for \(r\) with velocity equal to the speed of light

\[r = \frac{2GM}{c^2}\]

This gives the event horizon for any mass \(M\) . . . but maybe there are more requirements for event horizon? but it’s the formula for the Schwarzschild radius.

(c) if the rest energy of mass \(M\) was converted to a photon, what is it’s wavelength?

The rest energy is given by \(E=mc^2\) and the energy of a photon is \(E=h\nu = \frac{hc}{\lambda}\).

\[Mc^2 = \frac{hc}{\lambda} \\ \lambda = \frac{h}{Mc}\]

(d) For what mass does its equivalent wavelength equal the size within which light cannot escape?

\[\frac{2GM}{c^2} = \frac{h}{Mc} \\ M = \sqrt{\frac{hc}{2G}}\]

These are all fundamental constants so we can solve for

\[M = \sqrt{\frac{(6.626\times10^{-34})(3\times10^8)}{2(6.67\times10^{-11})}} \\ M = 3.86\times10^{-8} \text{ kg}\]

(e) What is the corresponding size?

\[r = \frac{2GM}{c^2} \\ r = 5.7\times10^{-35} \text{ m}\]

(f) What is the energy?

\[E = Mc^2 \\ E = 3.47\times10^{9} \text{ J}\]

(g) period?

\[T = \frac{1}{\nu} \rightarrow T = \frac{\lambda}{c} \\ T = 1.9\times10^{-43} \text{ s}\]

Problem 8