Problem Set 11

(14.1)

Do a Taylor expansion of equation (14.6) around V = 0.

Equation 14.6 states

$E \approx 2 E_F - 2 E_C e^{-2/(N_F V)}$

The Taylor expansion of $e^x$ about zero is

$e^x = \sum_{n = 0}^\infty \frac{x^n}{n!}$

$E \approx 2 E_F - 2 E_C \sum_{n = 0}^\infty \frac{1}{n!} \left( \frac{-2}{N_F V} \right)^n$

But this is an expansion around $V = \infty$ .

If you really want an expansion about $V = 0$ , note that

$\frac{d}{dx} e^{x^{-1}} = -x^{-2} e^{x^{-1}}$

As we keep taking higher derivatives we’ll get more and more negative powers of $x$ , but we’ll never get rid of the $e^{1/x}$ . So at $x = 0$ the latter term dominates, meaning the function and all its derivatives are zero. Thus the Taylor expansion about zero is identically zero.

Plugging this into equation 14.6 gives us the rather uninteresting

$E \approx 2 E_F$

(14.2)

Problem 6.5 showed that for a Kibble balance the current I measured in the dynamic phase and the voltage V measured in the static phase are related to the mass m, gravitational constant g, and velocity v by $IV = mgv$ . Using the inverse AC Josephson effect (equation 14.25) to determine the voltage, and the quantum Hall effect (equation 13.41) along with the inverse AC Josephson effect to determine the current, relate the measurement to fundamental constant(s).

In problem 6.5 in problem set 4 we found that

$m = -\frac{I V}{g v}$

The AC Josephson effect gives us a relation between voltage and frequency that only depends on fundamental constants (and n, a positive integer).

$V = n \frac{h}{2 e} f$

The quantum Hall effect can give us a resistance that only depends on fundamental constants (and i, a positive integer).

$R_H = \frac{h}{i e^2}$

By Ohm’s Law $IV = V^2/R$ , so the Kibble balance equation can be written as

$mgv = -\frac{V^2}{R}$

Plugging in the values above we find

$4mgv = -h i n^2 f^2$

(14.3)

If a SQUID with an area of $A = 1 cm^2$ can detect 1 flux quantum, how far away can it sense the field from a wire carrying 1 A?

As found in problem 6.4 in problem set 4, the magnitude of the magnetic field a distance $r$ away from an infinitely long and thin conductor carrying a current $I$ is $I/(2 \pi r)$ . One flux quantum is $\num{2.07e-7} \si{G \cdot cm^2}$ i.e. $\num{2.07e-11} \si{T \cdot cm^2}$ . So to get one flux quantum over $1 \si{cm^2}$ , we need a magnetic field of $\num{2.07e-11} \si{T}$ . Thus a one amp current can be detected at a distance of

$\begin{align*} r &= \frac{\mu_o I}{2 \pi B} \\ &= \frac{\num{1.26e-6} \si{T m / A} \cdot 1 \si{A}}{2 \pi \cdot \num{2.07e-11} \si{T}} \\ &= \num{9.66e3} \si{m} \end{align*}$

(14.4)

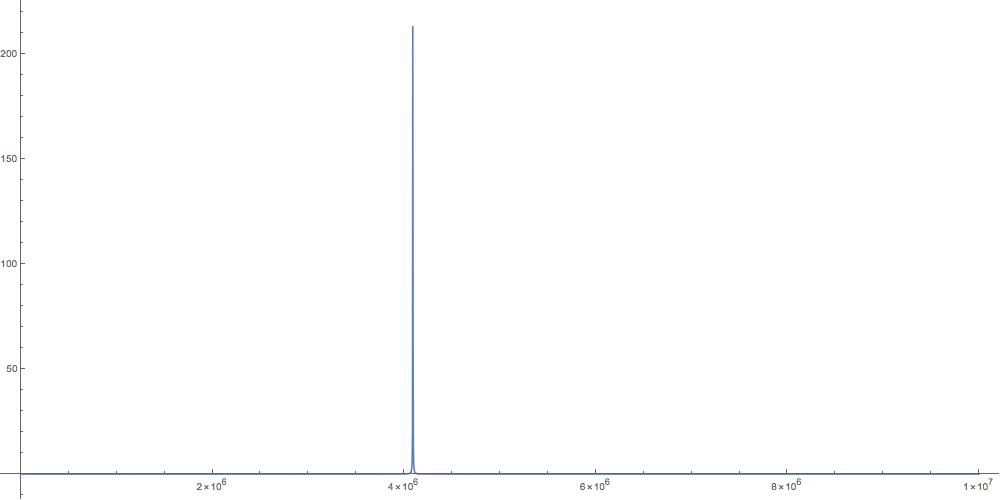
Typical parameters for a quartz resonator are $C_e = 5 \si{pF}$ , $C_m = 20 \si{fF}$ , $L_m = 3 \si{mH}$ , $R_m = 6 \si{\ohm}$ . Plot, and explain, the dependence of the reactance (imaginary part of the impedance), resistance (real part), and the phase angle of the impedance on the frequency.

The circuit in question is depicted in figure 14.4. There’s a capacitance $C_e$ in parallel with a series RLC circuit ( $R_m$ , $L_m$ , and $C_m$ ). To solve this it’s helpful to know the complex impedances of the basic electrical components:

$\begin{align*} Z_C &= \frac{1}{i \omega C} \\ Z_L &= i \omega L \\ Z_R &= R \end{align*}$

Then we just combine these, using the sum for series connections, and the inverse of the sum of inverses for parallel connections. So the total impedance $Z$ is

$\begin{align*} \frac{1}{Z} &= \frac{1}{Z_{C_e}} + \frac{1}{Z_{C_m} + Z_{L_m} + Z_{R_m}} \\ &= i \omega C_e + \frac{1}{1/(i \omega C_m) + i \omega L_m + R_m} \\ &= i \omega C_e + \frac{\omega C_m}{-i + \omega C_m (R_m + i \omega L_m)} \\ Z &= \frac{1}{i \omega C_e + \frac{\omega C_m}{\omega C_m (R_m + i \omega L_m) - i}} \end{align*}$

Let’s see what this looks like with the given values plugged in. All the x axes are in radians per second.

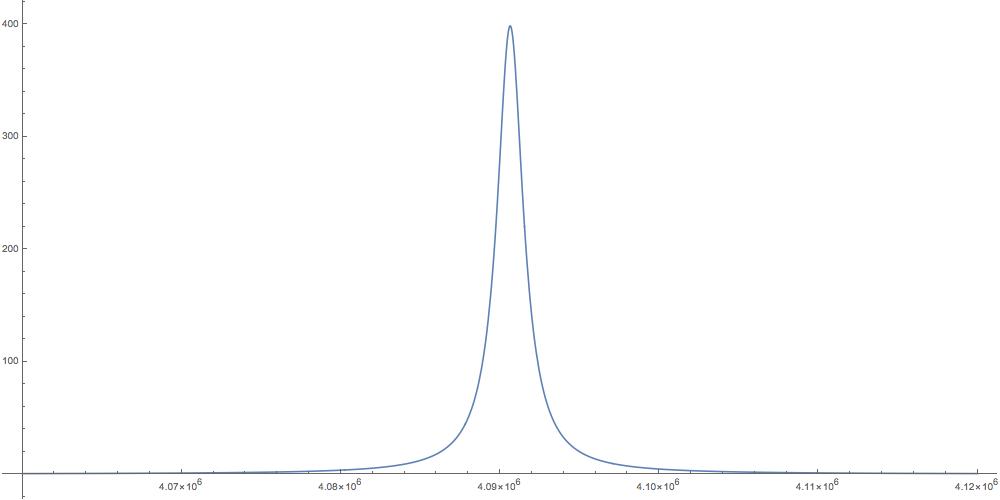
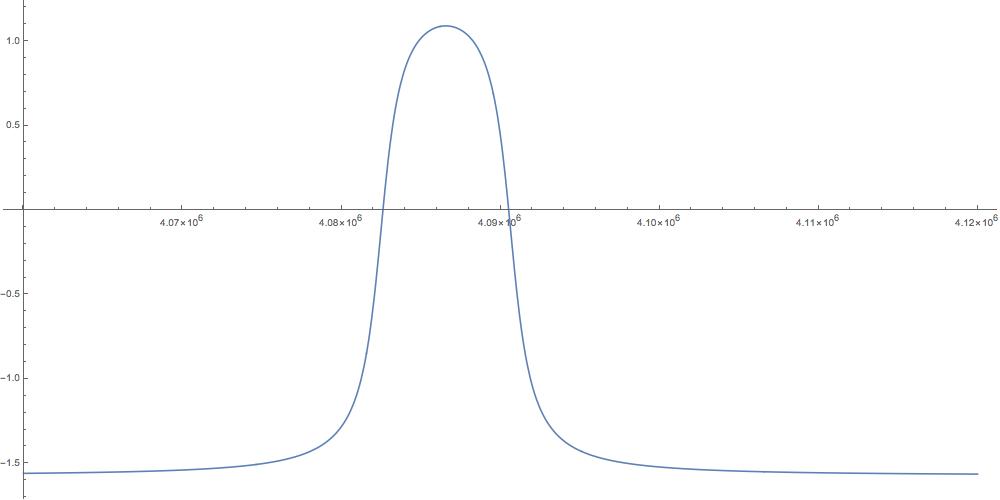
The resistance (real part) is very small except for a spike near $\num{4e6} \si{rad/s}$ .

resistance vs frequency

Mathematica tells me the max occurs at

$\begin{align*} \omega_\text{max} &= \frac{1}{L_m} \sqrt{\frac{2 C_e L_m + 2 C_m L_m -C_e C_m R_m^2}{2 C_e C_m}} \\ &\approx \num{4.09e6} \si{rad/s} \end{align*}$

But the first term in the numerator is a couple orders of magnitude larger than the others, so we can approximate $\omega_\text{max}$ by dropping them.

$\begin{align*} \omega_\text{max} &\approx \frac{1}{L_m} \sqrt{\frac{2 C_e L_m}{2 C_e C_m}} \\ &= \frac{1}{\sqrt{C_m L_m}} \\ &\approx \num{4.08e6} \si{rad/s} \end{align*}$

The reactance decreases without bound as $\omega$ approaches zero, and tends toward 0 as $\omega$ increases. It has a kink in about the same place the resistance has a spike.

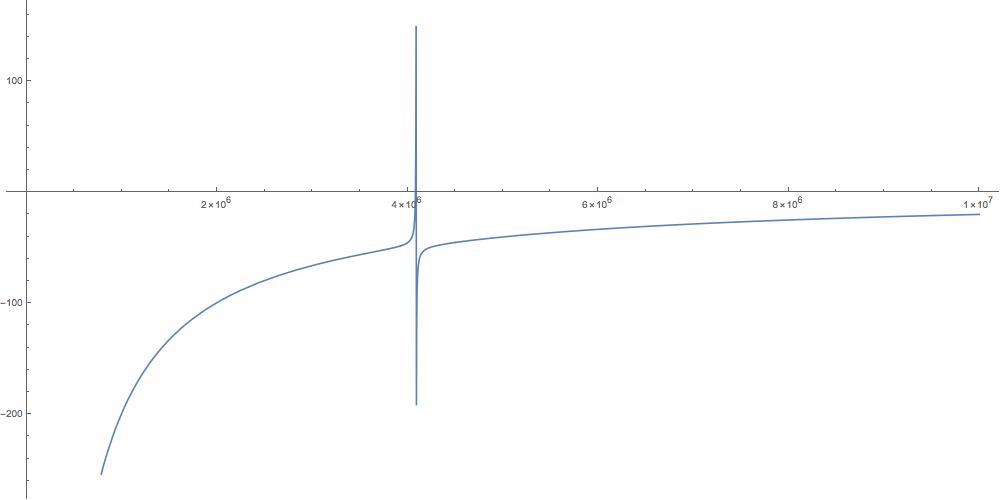
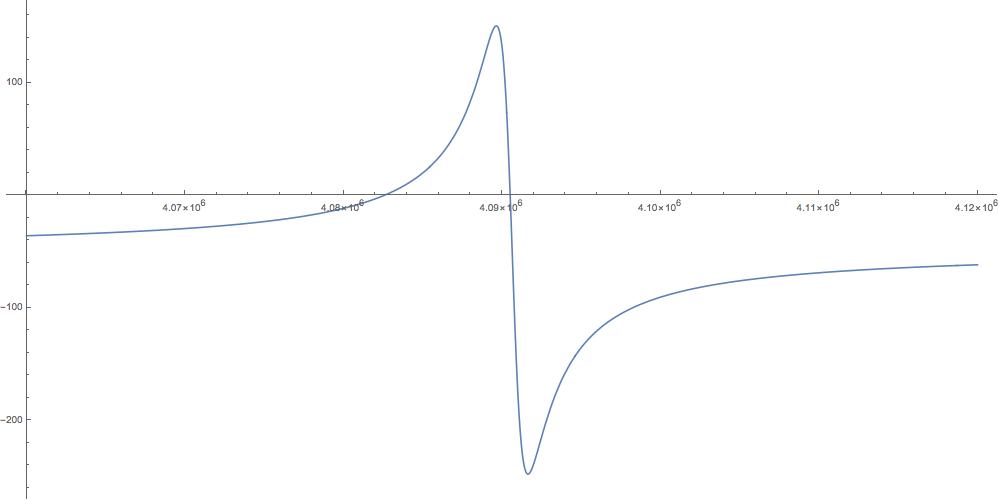
reactance vs frequency

Finally the phase is almost always $-\pi$ , except where it shoots just above one (radian), again near $\omega = 1/\sqrt{C_m L_m}$ .

phase vs frequency

Let’s zoom in on those spikes.

resistance vs frequency reactance vs frequency phase vs frequency

(14.5)

If a ship traveling on the equator uses one of John Harrison’s chronometers to navigate, what is the error in its position after one month? What if it uses a cesium beam atomic clock?

To solve this we need to know how many seconds are in a month.

$1 \si{month} \cdot \frac{30 \si{days}}{1 \si{month}} \cdot \frac{86400 \si{s}}{1 \si{day}} = \num{2.59e6} \si{s}$

Harrison’s chronometer has a relative error of $10^{-5}$ . So after a month it will be off by

$\begin{align*} \Delta t &= 10^{-5} \cdot \num{2.59e6} \si{s} \\ &= 25.9 \si{s} \end{align*}$

In Harrison’s time the only reference available to sailors at sea were the stars. Using a sextant you can measure the angle between a known astronomical object (say Alpha Andromedae) and the horizon. This tells you your angle relative to the stars. You want your angle relative to the Earth (i.e. longitude). So the missing information is the angle of the Earth relative to the stars. This you can compute if you just know what time it is (and the time of year).

But if your time measurement is off by $\Delta t$ , your estimate of the Earth’s angle will be off by $\Delta t \cdot v$ where $v$ is the speed of the surface of the Earth due to rotation. Assuming you did take a really accurate measurement of your own angle relative to the stars, this will be the same error in your estimate of your position relative to the Earth.

So first let’s find $v$ (at the equator).

$\begin{align*} v &= r \omega \\ &= r \cdot \frac{1 \si{rotation}}{1 \si{day}} \cdot \frac{2 \pi \si{rad}}{1 \si{rotation}} \cdot \frac{1 \si{day}}{86400 \si{s}} \\ &= \frac{2 \pi \cdot \num{6.37e6} \si{m}}{86400 \si{s}} \\ &= 463.3 \si{m/s} \end{align*}$

Then the error in the ship’s position measurement is

$\begin{align*} \Delta t \cdot v &= 25.9 \si{s} \cdot 463.3 \si{m/s} \\ &= 12 \si{km} \end{align*}$

If we instead use a Cesium clock, with a relative error of $10^{-12}$ , we’ll only be off by

$10^{-12} \cdot \num{2.59e6} \si{s} \cdot 463.3 \si{m/s} = 1.2 \si{mm}$

(14.6)

GPS satellites orbit at an altitude of 20,180 km.

(a)

How fast do they travel?

We need a relationship between orbital altitude and velocity. Consider a particle moving in a circle of radius $r$ , with angular velocity $\omega$ . We can model its trajectory as

$\begin{align*} x(t) &= r e^{i \omega t} \\ \dot{x}(t) &= i r \omega e^{i \omega t} \\ \ddot{x}(t) &= -r \omega^2 e^{i \omega t} \end{align*}$

The magnitude of its acceleration is $r \omega^2$ , so it experiences a force

$\begin{align*} F &= ma \\ &= m r \omega^2 \\ &= m \frac{v^2}{r} \end{align*}$

where the last line follows since $v = r \omega$ .

In this case we know $r$ (recall that the radius of the Earth is $\num{6.37e6} \si{m}$ ), and we can assume the only force is gravitational. Thus

$\begin{align*} \frac{G M m}{r^2} &= m \frac{v^2}{r} \\ v &= \sqrt{\frac{GM}{r}} \\ &= \sqrt{\frac{\num{6.67e-11} \si{m^3 kg^{-1} s^{-2}} \cdot \num{5.97e24} \si{kg}} {\num{6.37e6} \si{m} + \num{2.02e7} \si{m}}} \\ &= \num{3.87e3} \si{m/s} \end{align*}$

(b)

What is their orbital period?

$\begin{align*} T &= \frac{2 \pi r}{v} \\ &= \frac{2 \pi \left( \num{6.37e6} \si{m} + \num{2.02e7} \si{m} \right) }{\num{3.87e3} \si{m/s}} \\ &= \num{4.31e4} \si{s} \\ &= \num{11.96} \si{hours} \end{align*}$

(c)

Estimate the special-relativistic correction over one orbit between a clock on a GPS satellite and one on the Earth. Which clock goes slower?

We have already found the velocity of the satellite. As we found in the previous problem, the velocity of a clock on the surface of the Earth is $463.3 \si{m/s}$ . Thus the respective Lorentz factors are

$\begin{align*} \gamma_\text{Earth} &= \frac{1}{\sqrt{1 - (463.3 \si{m/s})^2 / (\num{3e8} \si{m/s})^2}} \\ &= 1 + \num{1.19e-12} \\ \gamma_\text{orbit} &= \frac{1}{\sqrt{1 - (\num{3.87e3} \si{m/s})^2 / (\num{3e8} \si{m/s})^2}} \\ &= 1 + \num{8.33e-11} \end{align*}$

So one day on the surface of the Earth is longer than one day at the center of the Earth by

$\begin{align*} \Delta t &= (\gamma_\text{Earth} - 1) \cdot 1 \si{day} \\ &= \num{1.19e-12} \cdot 86400 \si{s} \\ &= \num{1.03e-7} \si{s} \end{align*}$

And one day in orbit is longer than one day at the center of the Earth by

$\begin{align*} \Delta t &= (\gamma_\text{orbit} - 1) \cdot 1 \si{day} \\ &= \num{8.33e-11} \cdot 86400 \si{s} \\ &= \num{7.20e-6} \si{s} \end{align*}$

Similarly one orbital period on the surface of the Earth is longer than one orbital period at the center of the Earth by

$\begin{align*} \Delta t &= \num{1.19e-12} \cdot \num{4.31e4} \si{s} \\ &= \num{5.13e-8} \si{s} \end{align*}$

And one orbital period in orbit is longer than one orbital period at the center of the Earth by

$\begin{align*} \Delta t &= \num{8.33e-11} \cdot \num{4.31e4} \si{s} \\ &= \num{3.59e-6} \si{s} \end{align*}$

The latter is also a good approximation of the difference between a clock in orbit vs the surface of the Earth over one orbit. Technically speaking the surface of the Earth isn’t an inertial frame of reference, but relative to orbit it’s close.

(d)

What is the general-relativistic correction over one orbit? Which clock goes slower?

The general relativistic correction indicates that time passes more quickly in orbit than on Earth because the Earth’s gravitational field is stronger on the surface than in orbit. The difference over one day is

$\begin{align*} \Delta t &= \left(\frac{1 - \frac{GM}{rc^2}}{1 - \frac{GM}{r'c^2}} - 1 \right) \cdot 1 \si{day} \\ &= \left(\frac{1 - \frac{\num{3.99e14} \si{m^3/s^2}}{(\num{6.37e6} \si{m} + \num{2.02e7} \si{m}) \cdot (\num{3e8} \si{m/s^2})^2}}{1 - \frac{\num{3.99e14} \si{m^3/s^2}}{\num{6.37e6} \si{m} \cdot (\num{3e8} \si{m/s^2})^2}} - 1\right) \cdot 86400 \si{s} \\ &= \num{4.57e-5} \si{s} \end{align*}$

Similarly the difference over one orbital period is $\Delta t = \num{2.28e-5} \si{s}$ .