PIT 2022

Camron's course work for MAS.862 Physics of Information Technology

Final Project

AQFP readout with nanocryotron device

The goal of my final project was to determine the feasibility and limitations of using a nanocryotron (nTron) device as the readout mechanism for an Adiabatic Quantum Flux Parametron (AQFP) logic circuit. The AQFP is an ultralow power device (~1 zJ = \(10^{-21}\) J switching dissipation at 5 GHz) with high sensitivity (~10 uA in the circuits I’ve designed, but this can be pushed, as explore previously at YNU and MITLL). The output on a AQFP circuit is amplified from the input, but it’s still much to small to be read out by conventional CMOS transistors or room temperature measurement devices. Therefore, complicated readout amplifiers must be added to AQFP circuits in order to properly decode the digital output signal. These are typically DC readout SQUIDs (superconducting quantum interference devices) or a suzuki stack. These readout methods are costly in area, power, and complexity along with being very sensitive to noise. I would like to explore replacing the SQUID or suzuki stack with an ntron - a nanowire based switching device.

The basic operation of an nTron device is shown below. In summary it is a three-terminal voltage-level switching device that is made from a single layer thin film pattern, and therefore does not require any josephson junctions. The nTron uses an input gate current to induce a Joule-heated hotspot at a choke that connects the gate to a perpendicular superconducting channel. The hotspot causes a phase change from the superconducting to resistive state around the choke, and therefore modulates the current through the channel.

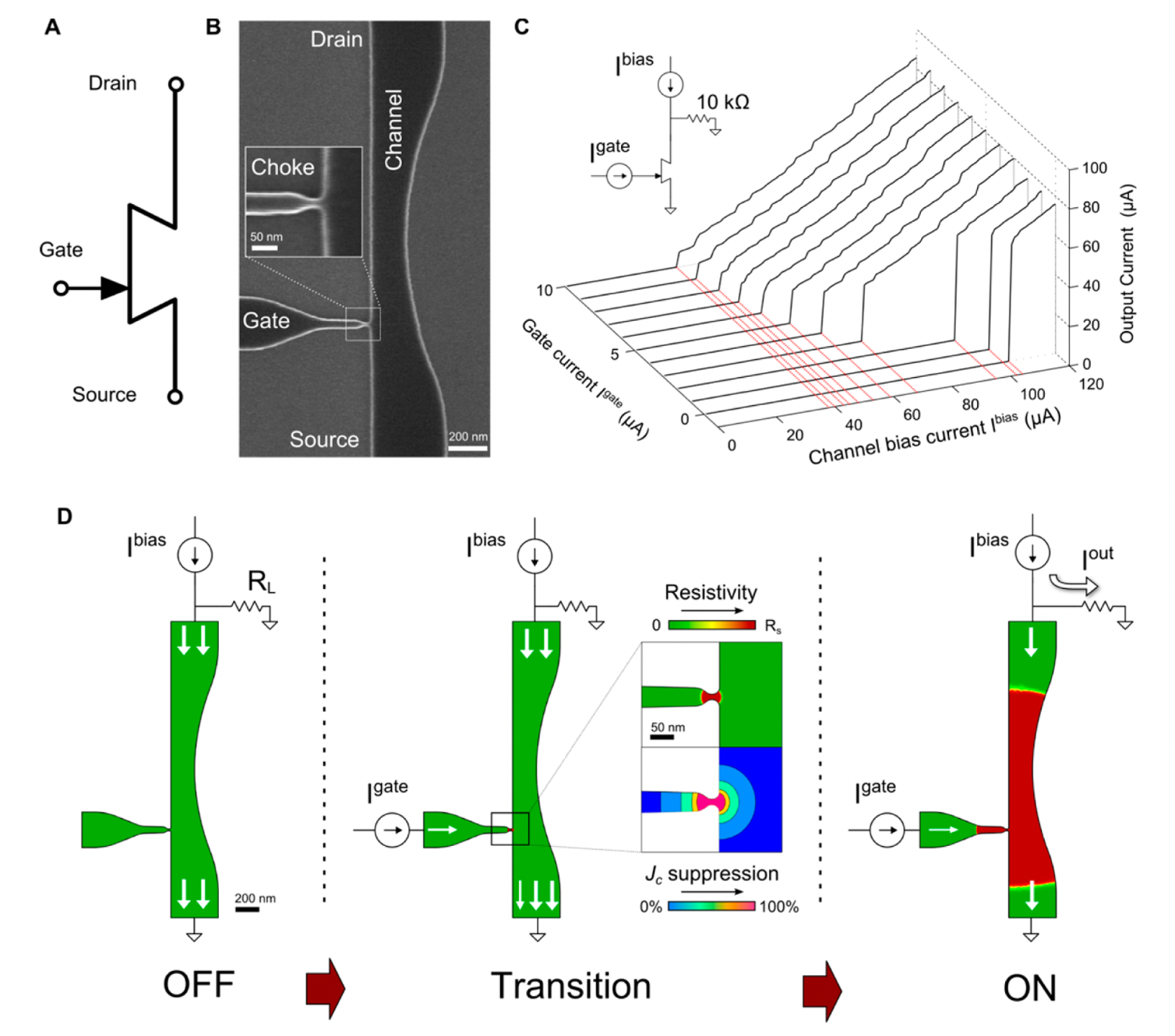nTron overview A. N. McCaughan and K. K. Berggren; A Superconducting-Nanowire Three-Terminal Electrothermal Device (2014); doi: 10.1021/nl502629x

The nTron has been used as a digital comparator for connecting Single Flux Quantum (SFQ) circuits to conventional CMOS systems previously.

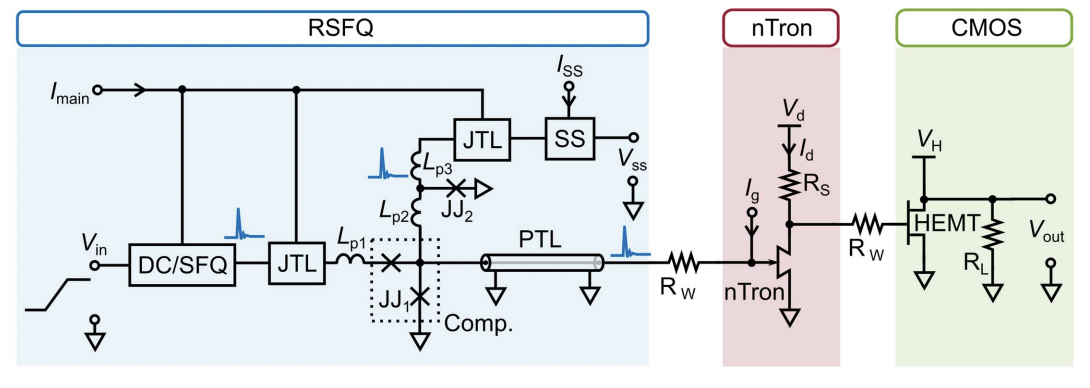SFQ nTron comparator Q.-Y. Zhao, et. al.; A nanocryotron comparator can connect single-flux-quantum circuits to conventional electronics (2017); doi: 10.1088/1361-6668/aa5f33.

This system can be split up into two different problems: the nTron sensing a SFQ pulse and then the nTron driving a COTs HMET transistor. For each of these tasks, the nTron needed to operate in different modes: the self-reset mode and the latched mode. These different modes have to do with how the nTron resets back into a superconducting state and depend on the current dynamics of the device - which can be described by a characteristic time constant \(\tau_e = L_{ch}/R_L\), where \(L_{ch}\) is the inductance of the nTron channel and \(R_L\) is the load resistance. If \(\tau_e > 10\)ns, then the current through the nanowire recovers slowly and the cooling of the substrate is able to overcome the joule-heating of the resistive state, so after a sharp pulse readout on the load resistor the nanowire resets itself back to the superconducting state. On the other hand, if \(\tau_e < 1\)ns, then the current changes quickly for the substrate cooling and joule-heated resistive spot to balance each other in equilibrium and therefore create a stable resistive state. In this case, the bias current on the nTron must be modulated to manually reset the device to its superconducting starting point.

The referenced paper demonstrates the nTron properly sensing SFQ pulses in the self-reset mode, where the ntron is hooked up to a 50\(\Omega\) amplifier at room temperature to confirm pulsed output. Then when the nTron needs to drive the high impedance transistor (1 k\(\Omega\)), it must operate in the latched mode due to the high resistive load, so an AC bias is used to reset the nTron after each SFQ pulse.

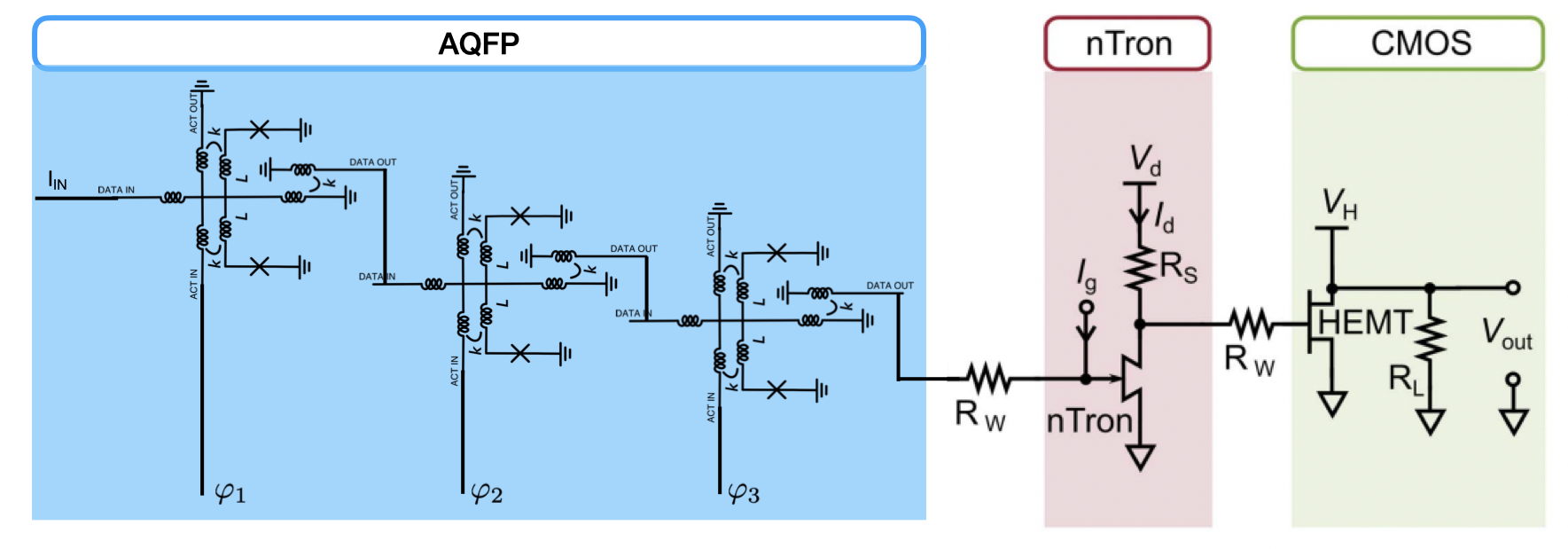
For this final project, I would like to simulate this similar circuit, expect replace the SFQ components with AQFP circuits.

page 1

I started by trying to simulate just the nTron device and to get a feel for how different bias currents and resisitive loads drive the behavior of the device. The QNN group has developed LTspice models for the nTron devices, which are basically the same as the SNSPD SPICE model described in K. K. Berggren et al., A superconducting nanowire can be modeled by using SPICE (2018); doi: 10.1088/1361-6668/aab149, with open source code here (the nTron model is modified for the three-terminal device with a choke, instead of a single nanowire).

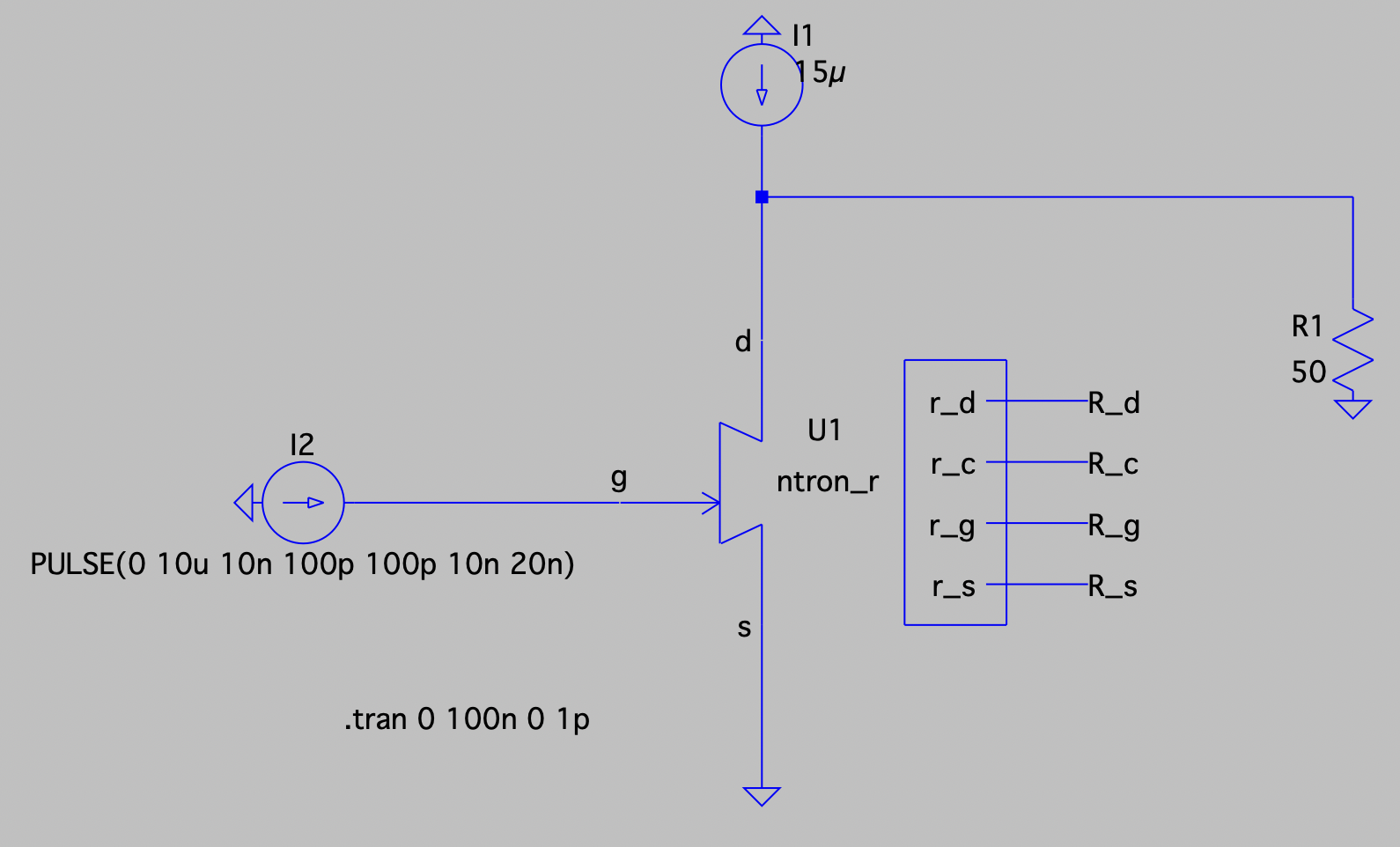
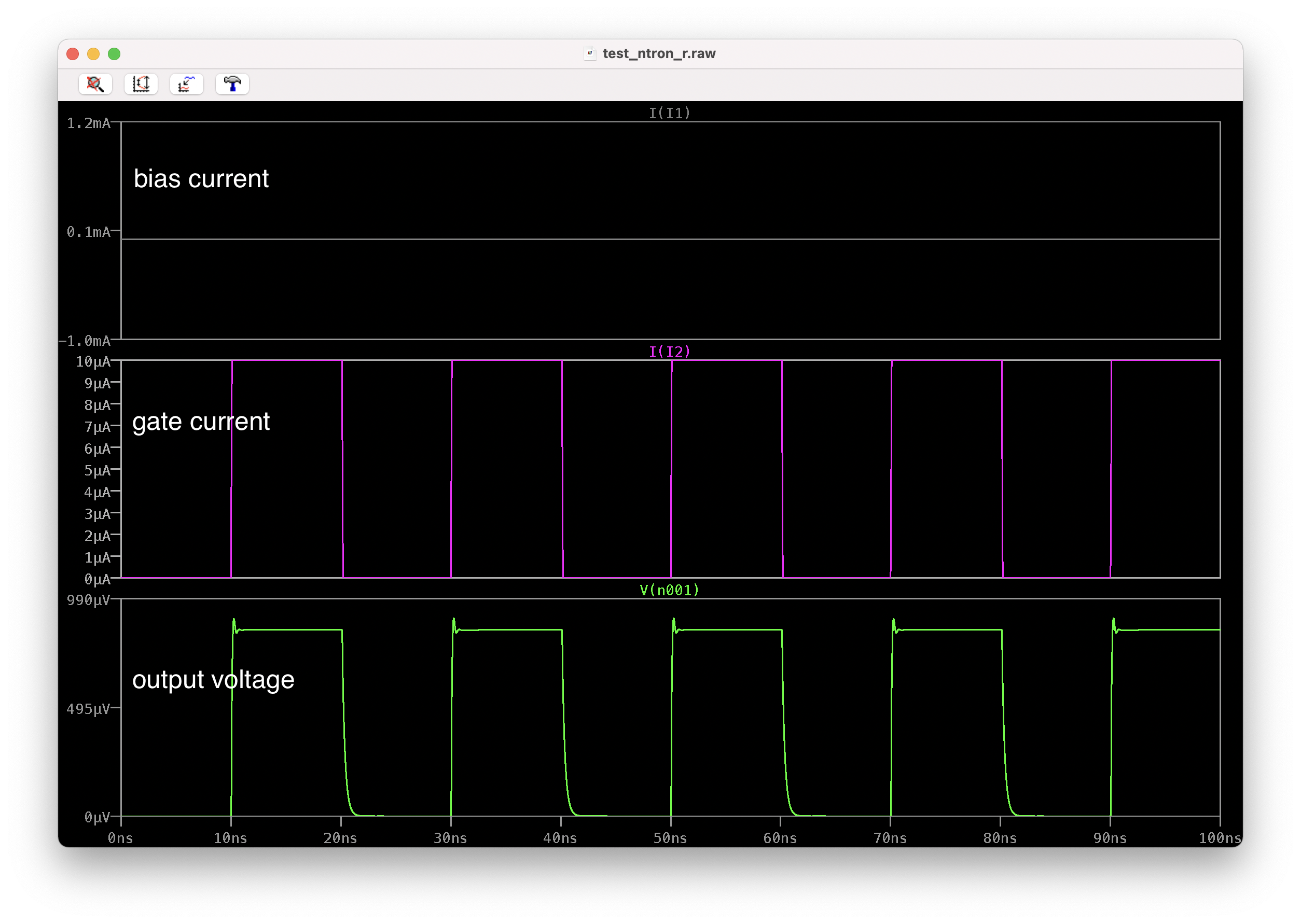
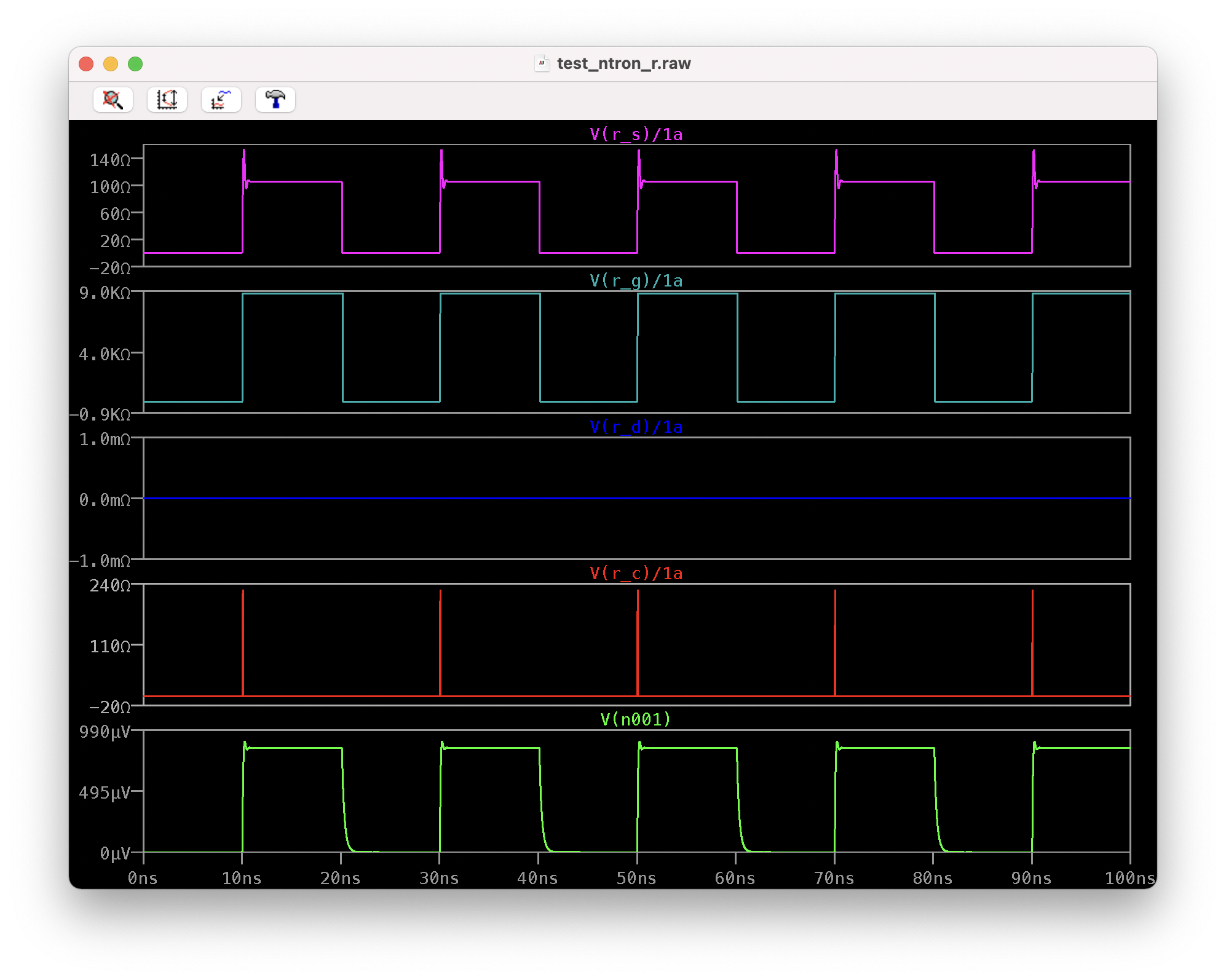
nTron schematic ntron output ntron output

The gate current input on this nTron is 10uA, and which matches nicely to the output from a basic AQFP buffer I’ve simulated in cadence.

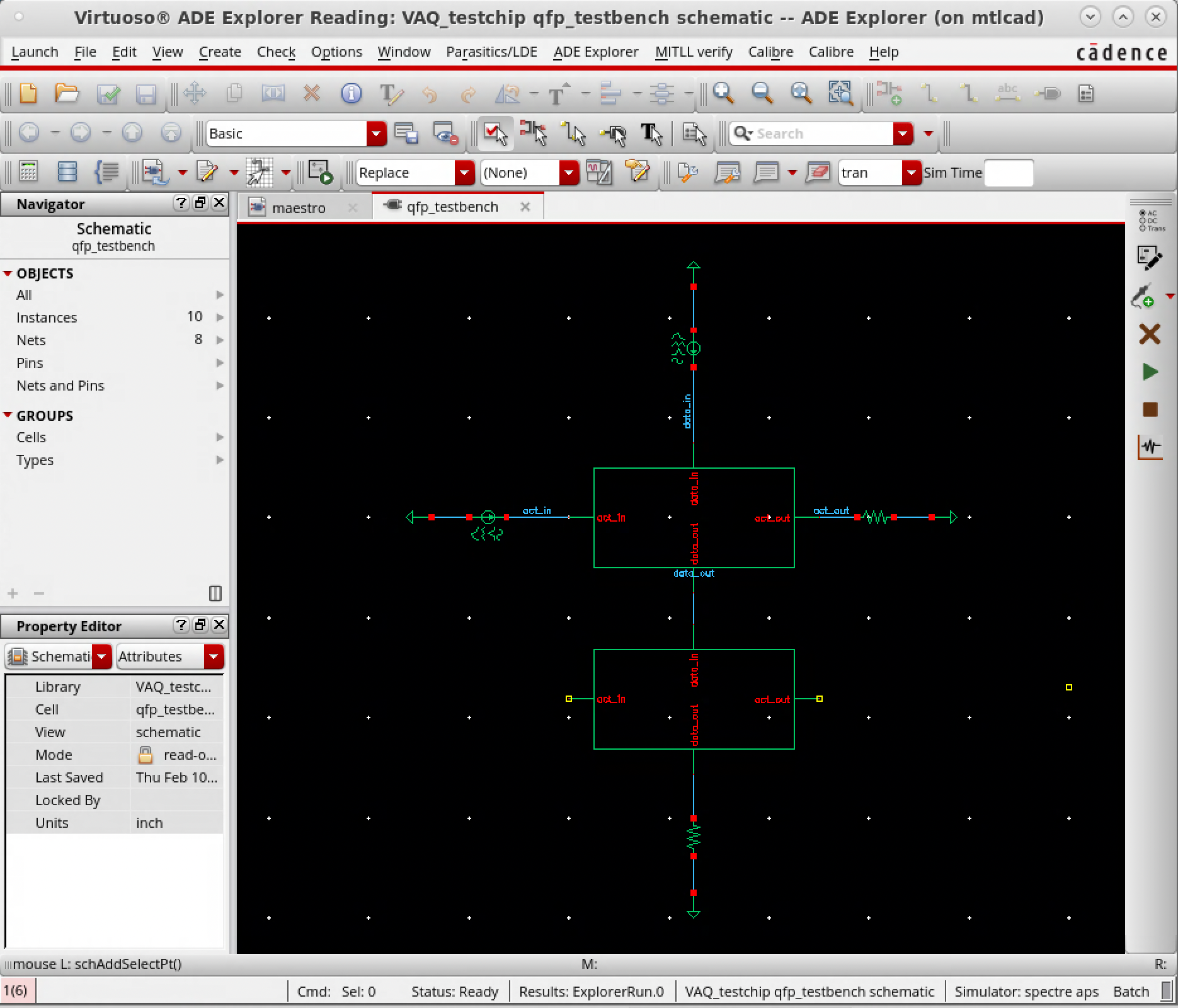
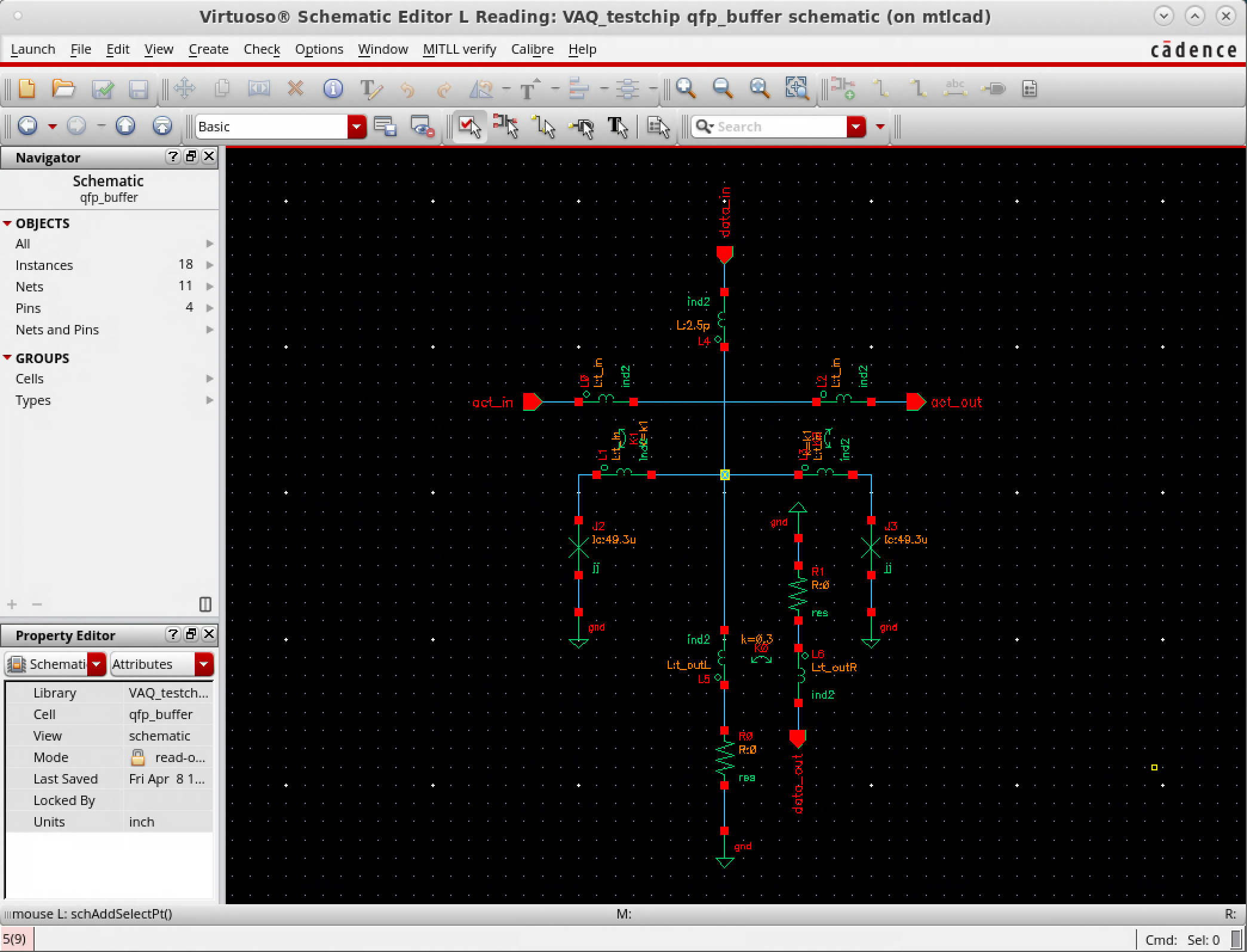
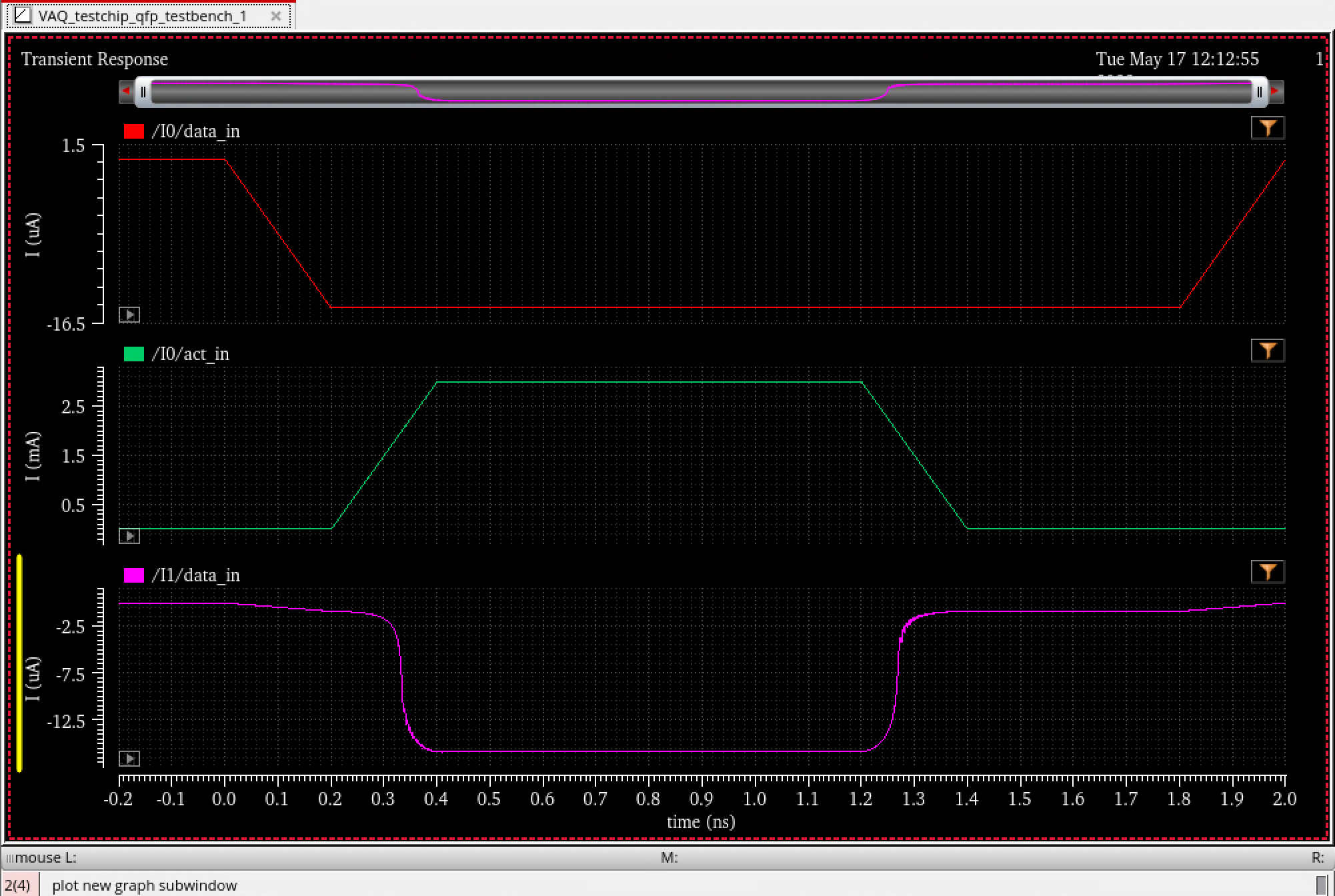
aqfp schematic aqfp schematic aqfp output

I have simple AQFP buffer circuits simulated in WRspice and Cadence, so the goal is to bring the nTron model into one of these platforms to be able to simulate the hybrid circuit in the same computational environment. There is a verilog-A version of an nTron simulation that was developed by BBN technologies for a previous superconducing digital logic program - this is what I would like to get running with the existing AQFP workflow I have.

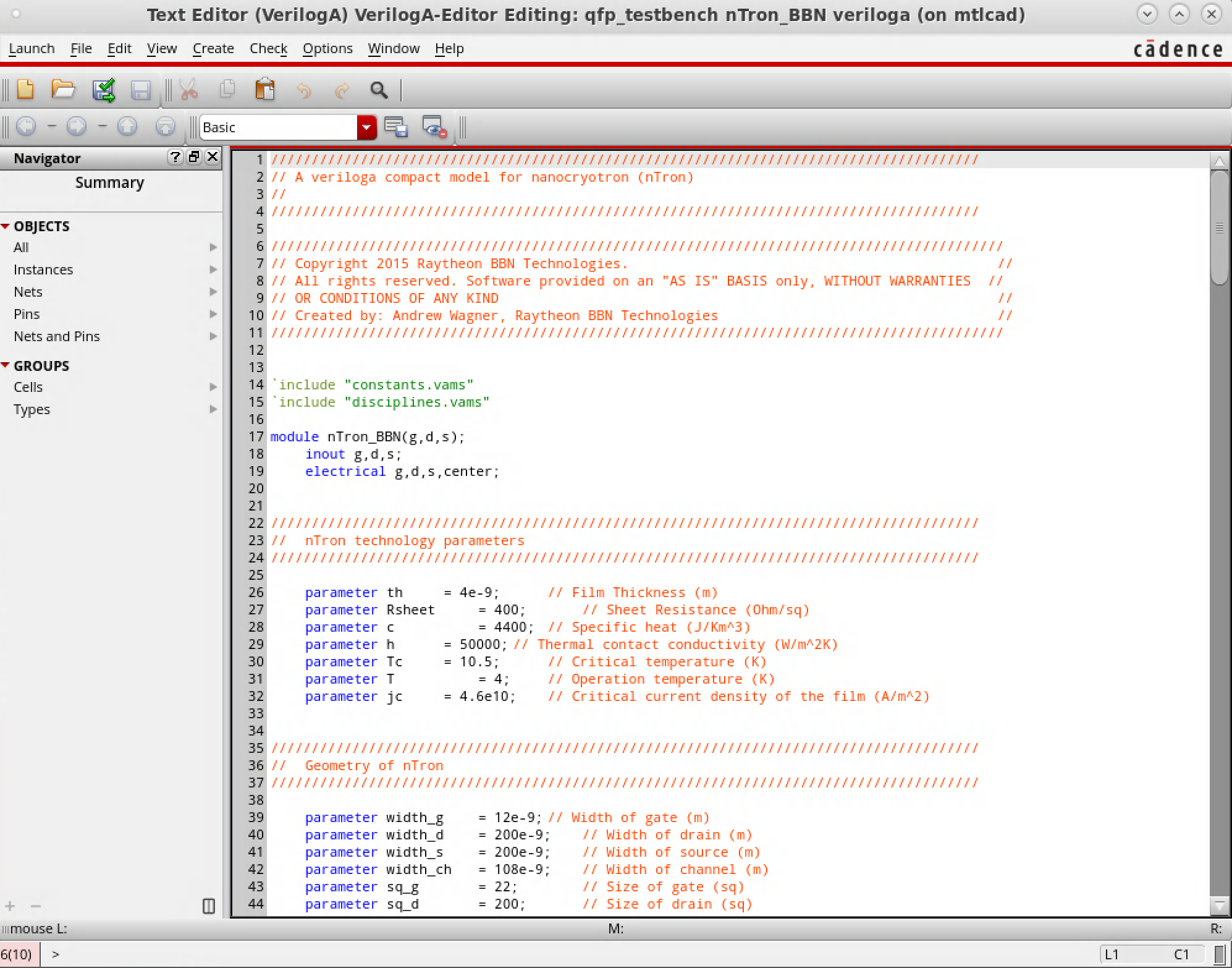
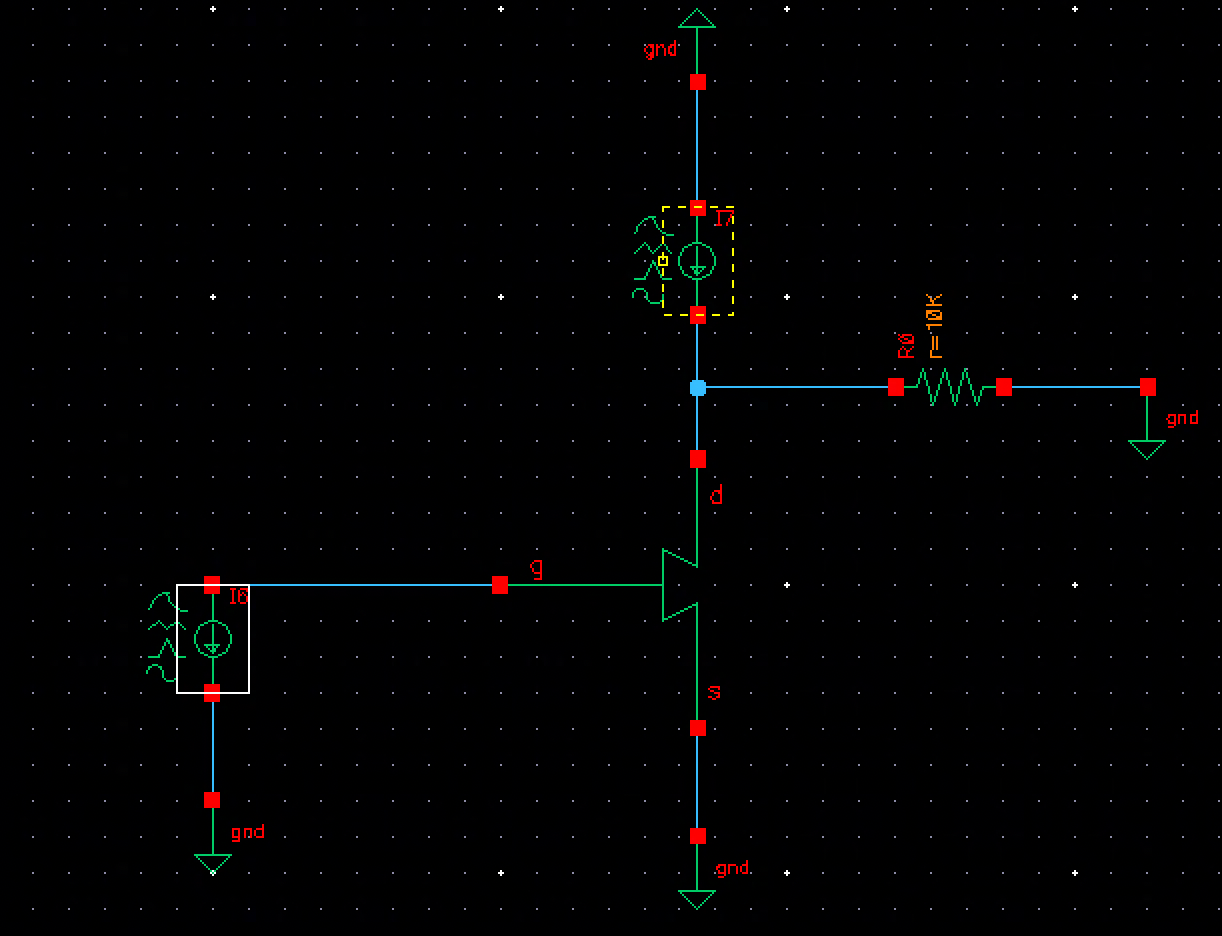
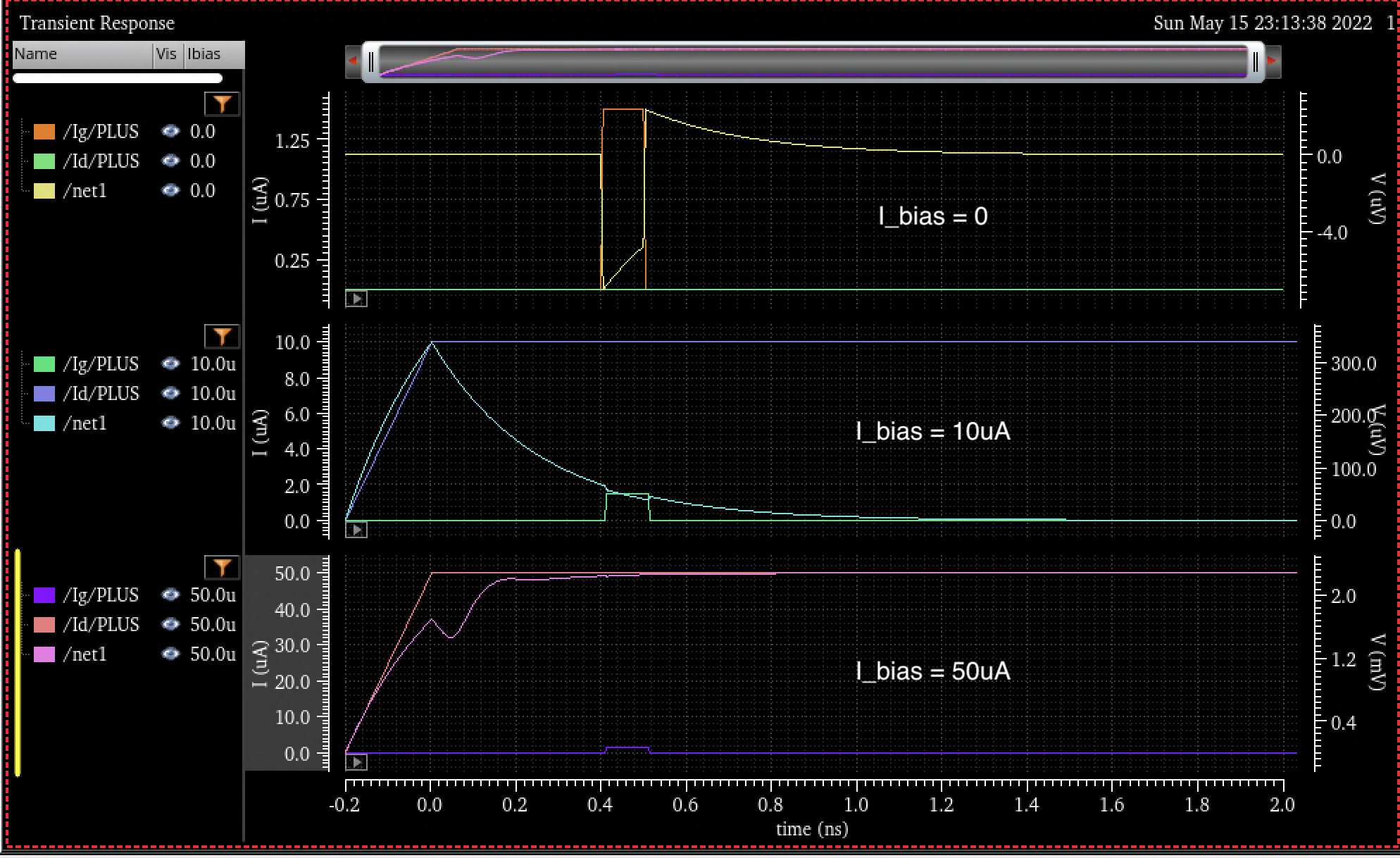
cadence nTron verilogA cadence nTron sch cadence nTron output

However, after a couple days of trying to get the nTron verilog-A model to run, I kept seeing unexpected behavior in the devices and couldn’t figure out what is going wrong. It felt uneccesary to continue struggling with this on my own, when I have plans later this week to work on this together with another researcher in the QNN group who has more experience modeling nTrons. Plus, this task has veered off course from the basic device physics overview that I wanted to do for RF SQUIDs and AQFPs. So I’ll pause nTron modeling for now and transition back to some fundamentals.

a work-in-progress exploration into superconducing loops

Final project questions:





older ideas

a dive into ~ QUANTUM COMPUTERS ~

The goal of my final project is for me to better understand the current state of the art in quantum computing. What types of devices are used? And how do they work? What’s the latest in quantum algorithms? How do the physical limits of computation, like landauer’s theorem, pertain to quantum information? I took a course on quantum information in undergrad and got a baby intro to it, but I’ve been rather out of the loop since than, and definitely forget most of the details. I’m curious about this topic again, because I’ve been looking at quantum computing as a relevant application for my research in utlra-low power classical superconducting circuits - future quantum copmuters will need classical components and it will be easiest if these components are co-located with quantum processors, most likely in cryogenic fridges – insert Super-DICE.

At the moment, I don’t have the most defined or contained question for a final project, but I feel I need to learn a bit about the area before I can really frame my “assignment” more concretely. So, I will start with a simple literature review. Since it’s such a hot tpoic, there have been a few great review articles on quantum computing over the last few years - I’ll start with these: