jerome arul

< back to main

i like triangles.

if you like triangles, you'll know that dividing a triangle creates smaller triangles within it.
sierpinski's triangle is a common "intro to visual coding" kinda thing.
i love how these recursive, self-similar triangles can unfold into a tree.

but does this work in 3 dimensions?
i haven't seen that before.
so can i make an unfurling tetrahedral tree for my final project?
and can i prototype the geometry and connections using flat material on the lasercutter?

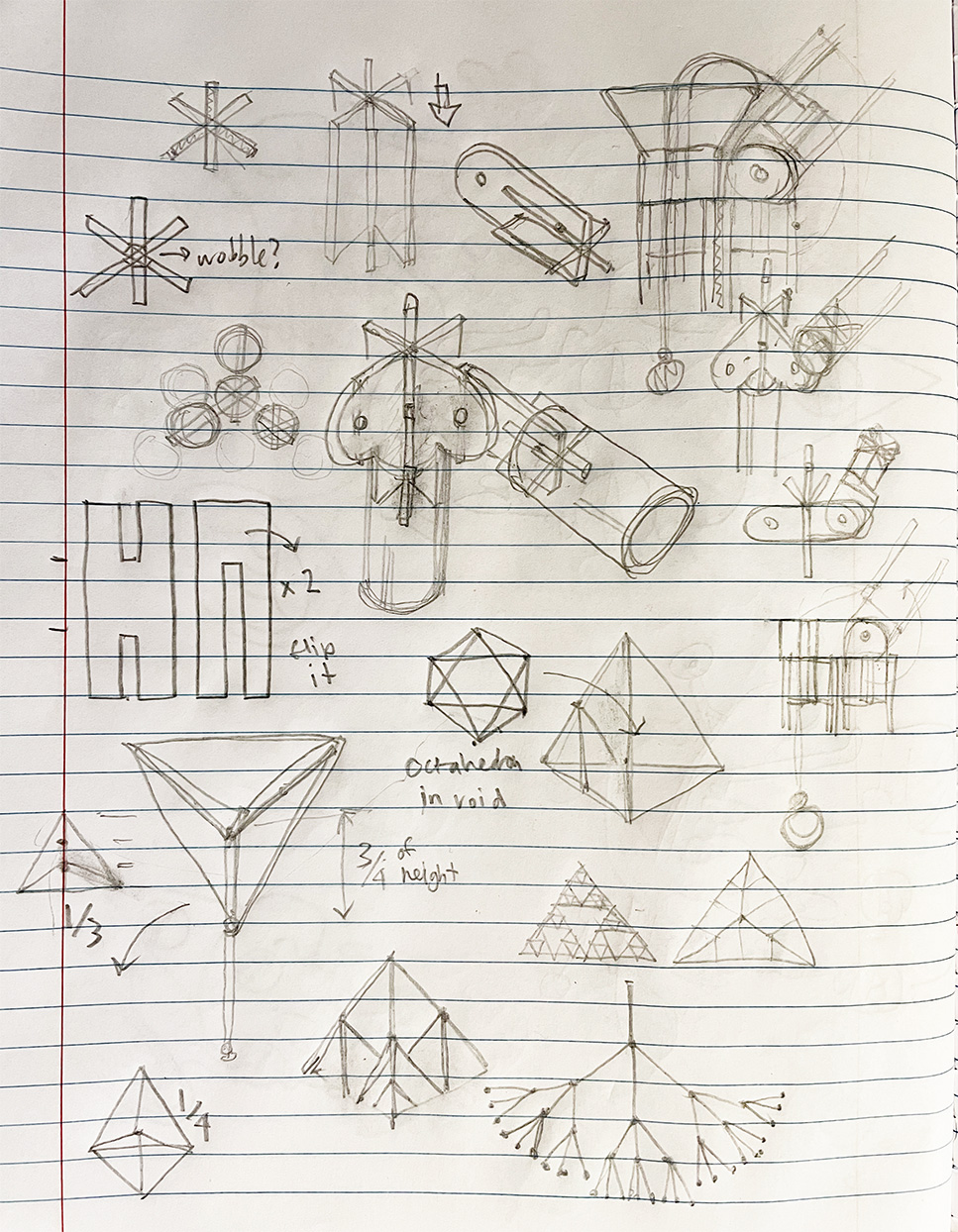
source: jerome's notebook

source: wikimedia - ruggiero

octet spaceframe in my backyard

this work builds off my thesis interests.
i have been building spaceframe structures using 3/4" conduit
and custom designed connectors (see wk 2.)

I referenced this "how to make struts" tutorial for diy geodesic domes.
the struts are simple to make with:
horizontal band saw
screw press
benchtop punch

i built a snub cube using the same method
for Tom Sachs' mit architecture I.S.R.U challenge

i now only use 5/16ths hardware for everything.

also. my "how make metal triangular polyhedra" youtube

tri-lap joint

tetra pods

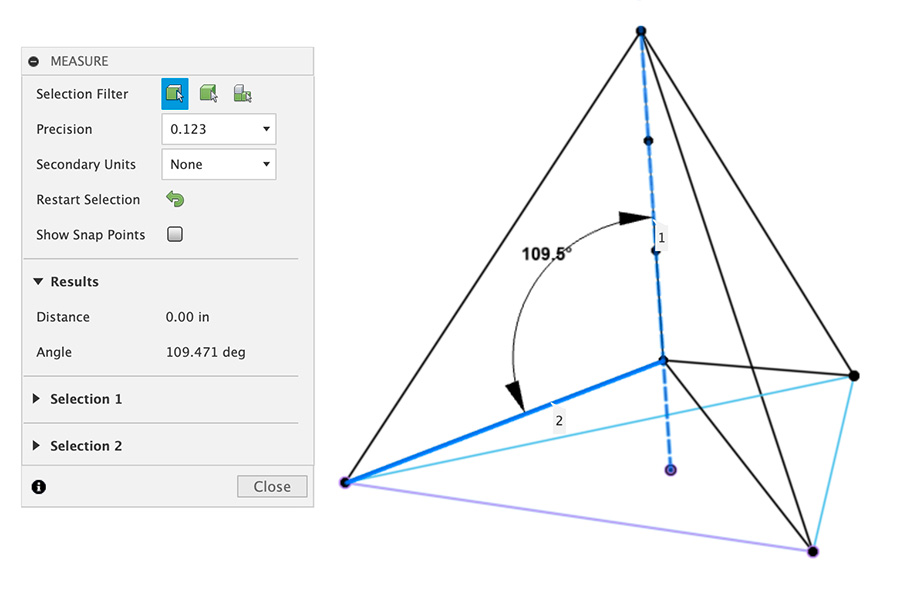
109.471 degrees

2x tetra / diamond cubic connectors

connected to 1" pvc

playing with tripod mechanism

umbrella mechanism

milling with soft jaws

tripod slip joint

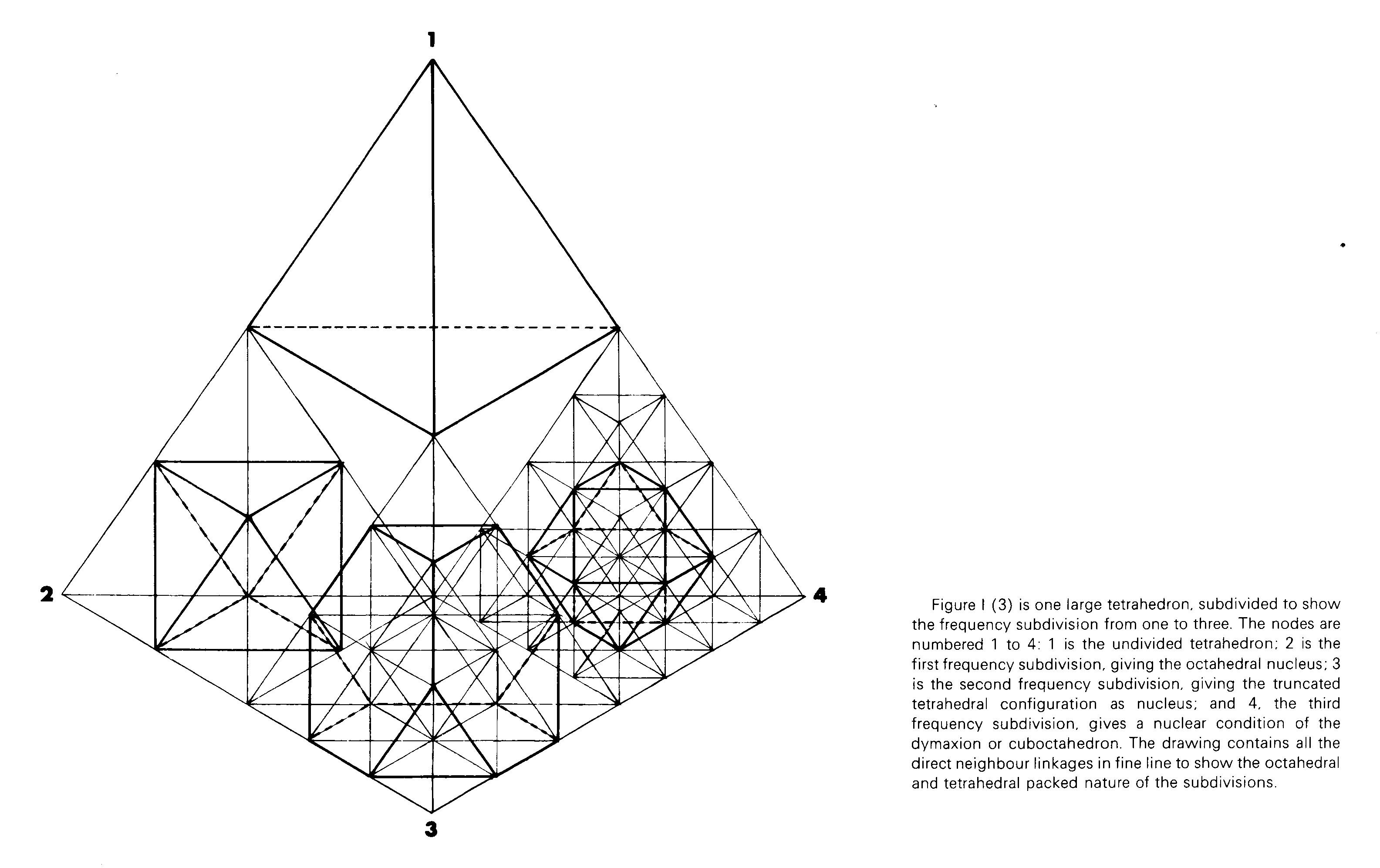
source: keith critchlow - order in space

divide a tetrahedron and you get smaller tets and an octahedron
divide again and you get even smaller tets and a truncated tet
divide again and you get a cuboctahedron
then you get a truncated octahedron (permutahedron-4)
then you get a truncated cuboctahedron
so on and so forth..

apparently a tetrahedron has a hausdorff dimension of 2.
- link ron eglash, chpt in african fractals.

how is a 3-dimensional object also a 2-dimensional fractal?

more dimensions?
the family of triangles in higher euclidean space
is the simplex.

- link > wheeler, geometrodynamics / gravitation deals with 4 and 5 simplices.
pg 472 dewitt / dewitt - relativity, groups and topology
bekenstein-bound > S= A/4 -> total entropy on a black hole's event horizon.

jakob schwichtenberg - physics from symmetry can derive particles and forces, but it cannot derive gravity, constants of nature, and also the number three. there are 3 gauges to 3 fundamental forces of the standard model, 3 lepton generations...etc