Concepts (ISQ, SI, and NIST)

The International System of Quantities

A base quantity is defined as a measurable property of a physical system that cannot be expressed in terms of other physical quantities. Every quantity in the system can be epxressed in terms of some combination of the base quantities.

In the International System of Quantities, there are seven base quantities:

  1. Length
  2. Mass
  3. Time
  4. Electric current
  5. Thermodynamic temperature
  6. Amount of substance
  7. Luminous intensity

The dimension of these physical quantities do not themselves have magnitude or units. The International System of Units (SI) assigns to each of these quantities a base unit that establishes a fundamental unit of measurement. These are the very familiar:

  1. Meter
  2. Kilogram
  3. Second
  4. Ampere
  5. Kelvin
  6. Mole
  7. Candela

Redefining Measures

To create a standard measurement system, we must agree to accept some arbitrary definition of a set of quantities. As discussed previously, this began with physical reference objects such sticks, feet, and pendulums, as far back as the 4th millenia BC. In fact, this phenomenon remained up until 2019, on the 144th anniversary of the Metre Convention, when all seven base units were re-defined in terms of fundamental universal constants (which were themselves arbitrarily defined at this time).

Previously, the definition of the kilogram was set to be exactly the mass of the International Prototype of the Kilogram (IPK), a cylindrical object made of a platinum-iridium alloy stored in a vault in Paris.

IPK

However, there were two issues with this definition. The first was that nobody had access to the IPK in order to make more identical copies of the kilogram to distribute the standard reference for mass. Secondly, and more critically, the mass of the IPK itself was changing over time. Since the kilogram was defined to itself be the mass of the IPK, that means that the value of a kilogram was unstable over time.

As a second-order effect, the definition of the mole, ampere, and candela were defined using the notion of the gram, newton, and watt respectively. All three of these units relied on the definition of a kilogram, meaning that the instability of the mass of the IPK implied an instability of the base units for four of the seven base quantities in the ISQ.

To solve this issue, on May 20th 2019, the values of kilogram, ampere, kelvin, and mole were redefined, based on a more fundamental redefinition of ‘universal constants’ to fixed values:

  1. The Planck constant $h$ is exactly $6.62607015×10^{−34} $ joule-second (J⋅s).
  2. The elementary charge $e$ is exactly $1.602176634×10^{−19}$ coulomb (C).
  3. The Boltzmann constant $k$ is exactly $1.380649×10^{−23}$ joule per kelvin (J⋅K $^{−1}$ ).
  4. The Avogadro constant $N_A$ is exactly $6.02214076×10^{23}$ reciprocal mole (mol $^{−1}$).

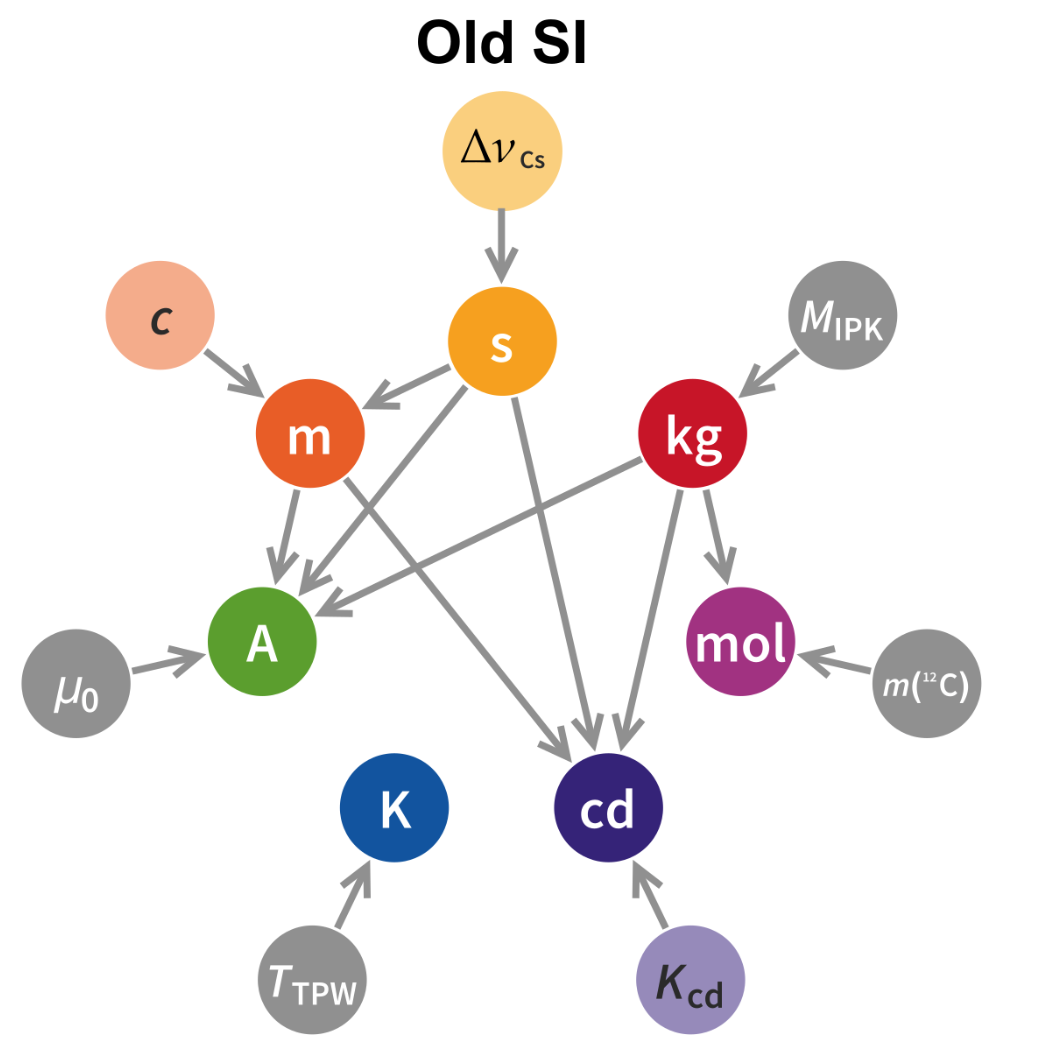
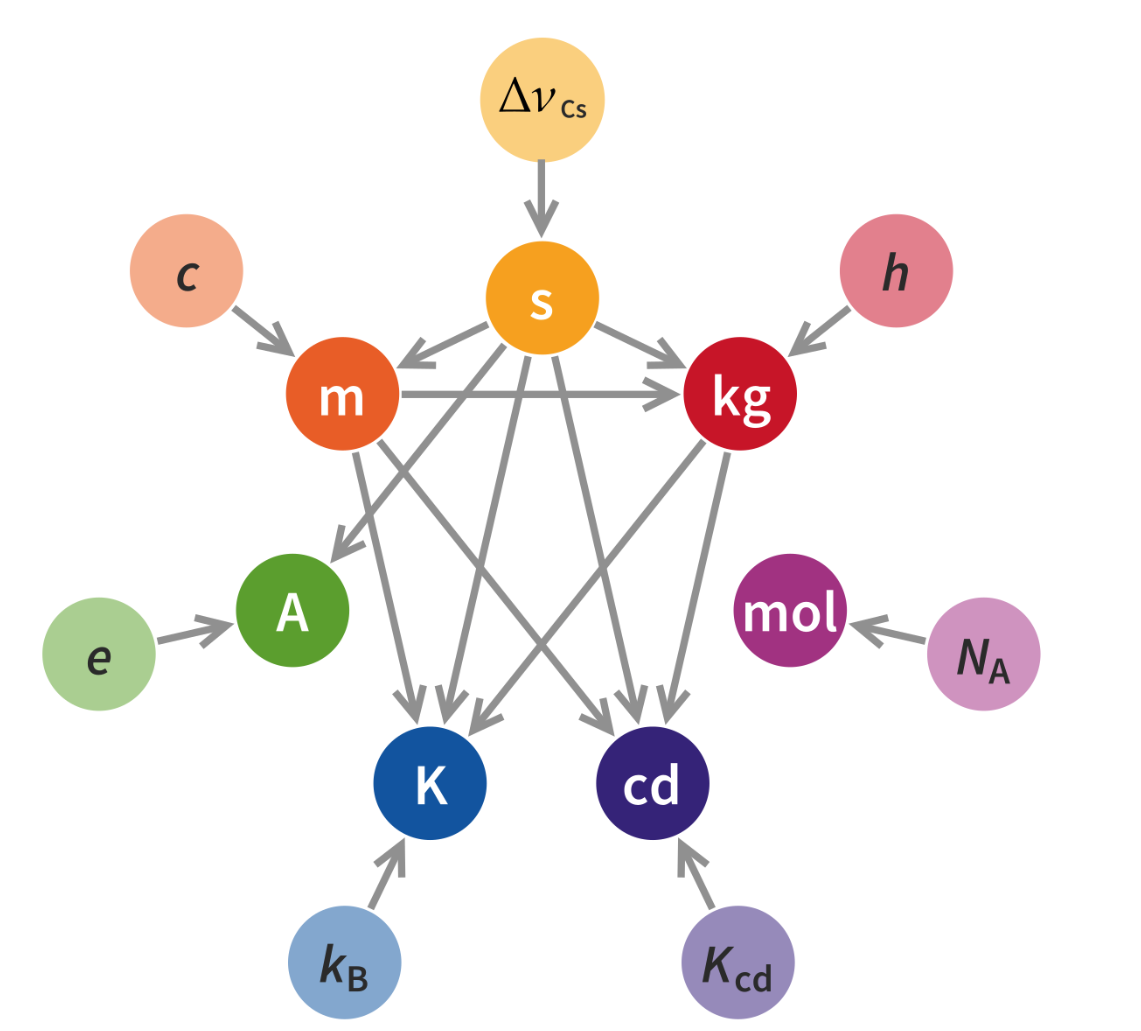
alt text

alt text

Now, the definitions of the base units of the SI system are given by the following:

  1. Second - the second is defined by taking the ground-state hyperfine transition frequency of Cs-133 to be 9192631770 Hz: \(1 s = \frac{9192631770}{\Delta v_{Cs}}\)
  2. Meter - the meter is defined by taking the speed of light to be 299792458 m/s, where the second is defined as above: \(1m = \frac{9192631770}{299792458} \frac{c}{\Delta v_{Cs}}\)
  3. Kilogram - the kilogram is defined by taking the Planck constant to be $6.62607015 \times 10^{-34}$ kg • $m^2$ • $s^{-1}$, where the meter and second are defined as above: \(1kg = \frac{(299792458)^2}{(6.62607015 \times 10^{-34})(9192631770)} \frac{h \Delta v_{Cs}}{c^2}\)
  4. Ampere - the ampere is defined by taking the value of the elementary charge of an electron to be $1.602176634 \times 10^{-19}$ A•s: \(1 A = \frac{1}{(1.602176634 \times 10^{−19})(9192631770)} e \Delta v_{Cs}\)
  5. Kelvin - the kelvin is defined by taking the value of the Boltzman constant to be $1.380649 \times 10^{-23}$ kg • $m^2$ • $s^{-2}$ • $K^{-1}$: \(1 \mathrm{~K}=\frac{1.380649 \times 10^{-23}}{\left(6.62607015 \times 10^{-34}\right)(9192631770)} \frac{h \Delta v_{\mathrm{CS}}}{k} .\)
  6. Mole - the mol is defined by taking the value of the Avogadro constant to be $6.02214076 \times 10^{23}$ elementary entities: \(1 \mathrm{~mol}=\frac{6.02214076 \times 10^{23}}{N_{\mathrm{A}}} .\)
  7. Candela - the candela is defined by taking the fixed numerical value of the luminous efficacy of 540 THz radiation, $K_{cd}$, to be 683 cd⋅sr⋅$kg^{−1}$⋅$m^{−2}$⋅$s^{3}$: \(1 \mathrm{~cd}=\frac{1}{683\left(6.62607015 \times 10^{-34}\right)(9192631770)^2} K_{\mathrm{cd}} h\left(\Delta v_{\mathrm{Cs}}\right)^2\)

The Kibble Balance

Now that all base units are defined in terms of fundamental universal constants, creating unit standards can be performed by first measuring those constants and then using those measurements to create devices or objects that allow one to derive the base units.

Perhaps the most important example of this is the Kibble balance, which is an instrument that enabled the replacement of the IPK and currently enables the manufacture of standard kilograms. The 4th generation Kibble balance, built at NIST (and replicated at NPL in the UK and BIPM in France), was able to measure the Planck constant to within 13 parts per billion, and can measure the mass of a kilogram to within 13 micrograms.

Kibble balance 3

Kibble balance & friends

The Kibble balance makes a measurement of mass in the following steps:

  1. Current $I$ is passed through a coil of length $L$ in a magnetic field until its balances a test mass $m$ in a gravitational field $g$; this current is precisely measured. \(mg = BLI\)
  2. To avoid necessitating the measurements the magnetic field and coil length, the coil is moved through the same field at a constant, known speed $v$. This induces a potential difference $V$ across the coil, which can then be measured. \(V = BLv\)
  3. These equations can be combined such that: \(m = \frac{UI}{gv}\)

With precise measurements of the potential difference, the current, $g$, and the velocity of the coil, we get a precise measurement of the mass $m$. This is dependent on the Planck constant being fixed, as that is what allows for the measurement of $V$ and $I$, since those are taken using quantum devices that are dependent on the Planck constant: the Josephson effect for measuring potential difference:

\[V = \frac{h}{2e} f = \frac{1}{K_J} f\]

where $f$ is a known frequency used to create the potental difference across a Josephson junction, and the quantum Hall effect for measuring resistance (and thus current):

\[R_H = \frac{h}{e^2}\frac{1}{n}\]

where $n$ is the known carrier density of a semiconductor used to create the quantized Hall resistance $R_H$. The relationship is given as:

\[h = \frac{4}{K_J^2 R_H}\]

A measurement of $K_J^2$ and $R_H$ can be used to determine the Planck constant experimentally; conversely, fixing the Planck constant allows for the determination of $K_J$ and $R_H$, which can then be used for measuring $V$ and $I$, which then allow for the measurement of $m$.