 Topics for the semester
Topics for the semester
 introduction introduction
|
|||||
 assignments assignments
|
|||||
 readings readings
|
|||||
 projects projects
|
|||||
 pictures pictures
|
Assignment 2: Demonstrate through an experiment or simulation an instance of "Threshold theorem" in any a field of your own choice : 20 Feb 2004
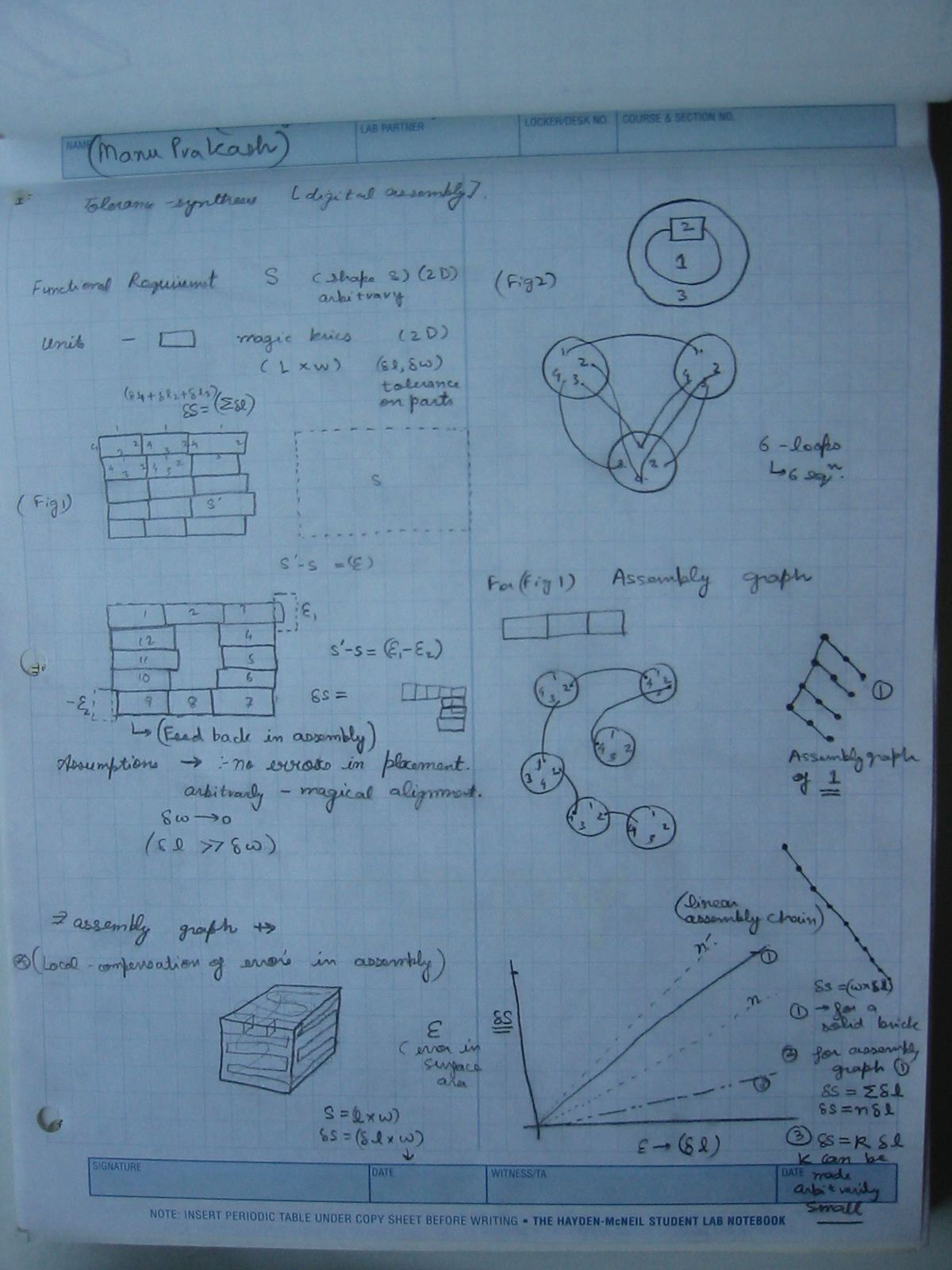
Examples could be from coding theory, error correcting fabrication, computation in presence of errors etc.For this assignment I took my stand on threshold theorem for fabrication. Thus given a set of faulty (parts which are not exact but have a tolerance limit), how would you build a system that meets the functional requirements of the system with a defined error (epsilon). I show a general assembly sequence where error grows linearly while we can be smart about the assembly graph and use notions of feedback to reduce this error rate. With increasing errors, there is a set point beyond which the error is unboundable
Consider a system of assembly task, where the functional requirement is a function of components making the part.
ie. S=f(x1,x2,x3..)
For the example of this assignment we will be considering S to be a given 2D shape. Let us cosider a rectangular shape for this analysis. The goal of the fabrication process is to produce the shape S, as close as possible.
We first define a "brick" as defined as rectangular piece which is a single unit of the assembly. The tolerance is bounded by del (l), where we assume for this analysis there is no error in height ie. del(w)=0, where del(x) is tolerance in that axis.
Process 1. Use a "brick" as large as the shape. In the graph you see
del(S)= w x del(l), which is linear in error in length.
Process 2. We use a ssembly process starting with brics smaller in size to the shape S, and align them based on there faces (defined as 1,2,3,4). Thus the seembly graph used for this process is shown in figure.
Here, clearly, del(S) = w x sigma del(l); for n parts used in assembly. With more number of parts, the error keeps increasing. This is true for many systems, where as the complexity of a mechanical system increases (more number of parts), harder (costly) it is to maintain the functional requirement. Assembly garph for this assembly is shown in figure.
Process 3 We use a smart way of assembly with feedback involved. The assembly graph is linear this time, as seen in figure. But we also keep minimizing the errors during the assembly process, by evaluating ( S-S' ) (where S is FR and S' is shape obtained). This brings
del(S) = w x K x (del L), where K is a constant which can be made smaller by choosing the right number of parts. Thus error in FR ie. (S - S') is made much smaller. The threshold is shown when del (L) starts to get much bigger than the shape S itself. Then the error becomes unbounded and we can not keep it down.
The error in FR vs. tolerance in "L" of the bric is shwon in figure. The following notions are defined in the figure below
1. Feedback in assembly
2. Assembly Graph
References :
1. Tolerance Synthesis Sceheme , NISTIR6836 U.Roy et al.
2. A Mathematical Model of Geometric Errors in the Case of Specification and 3D Control of Mechanical Parts ; Advanced Mathematical & Computational Tools in Metrology IV ;E. Ballot et al.