Optimal Control Theory

The systems we’ve described so far are fairly simple (though applicable to many many many things!)

Let’s say we want to get more complex and think about things like being energy efficient or fast… We quickly arrive at some flavor of underactuated systems: a lot of systems are actually underactuated— the most general definition of this is that you can’t arbitrarily generate inputs u to produce desired accelerations in all of your DOFs. So if you’re operating in a regime where torque limits matter, etc. the system may be underactuated (even tho you have actuators for all your DoFs).

When thinking about optimal control theory, we’re thinking about how we can work with the dynamics of our system, instead of using controls to override those dynamics [https://underactuated.csail.mit.edu/intro.html].

This means we might need to have some sense of our dynamics. So, from here on out, as it may have been before, we’re living in ODE and matrix land.

Want a refresher? NMM text book https://fab.cba.mit.edu/classes/864.23/index.html (Neil’s math class).

This chapter from the underactuated textbook will intro the motivation behind this: https://underactuated.csail.mit.edu/dp.html and also includes an example I like of deriving the optimal (min time) control policy for “the double integrator” (i.e. a frictionless sliding brick… or perhaps a linear axis?) which is… a bang bang policy.

We’re also going to be focusing on a specific model system, the Pendubot (aka the less popular cousin of the Cartpole and Acrobot). The Pendubot is a double pendulum with an actuator at the shoulder (base link), and a no actuation at the shoulder. (In contrast, the acrobot has an actuator at the elbow and not at the shoulder— this is the usual double pendulum underactuated system you’ll see everywhere) (but not here… 🤘).

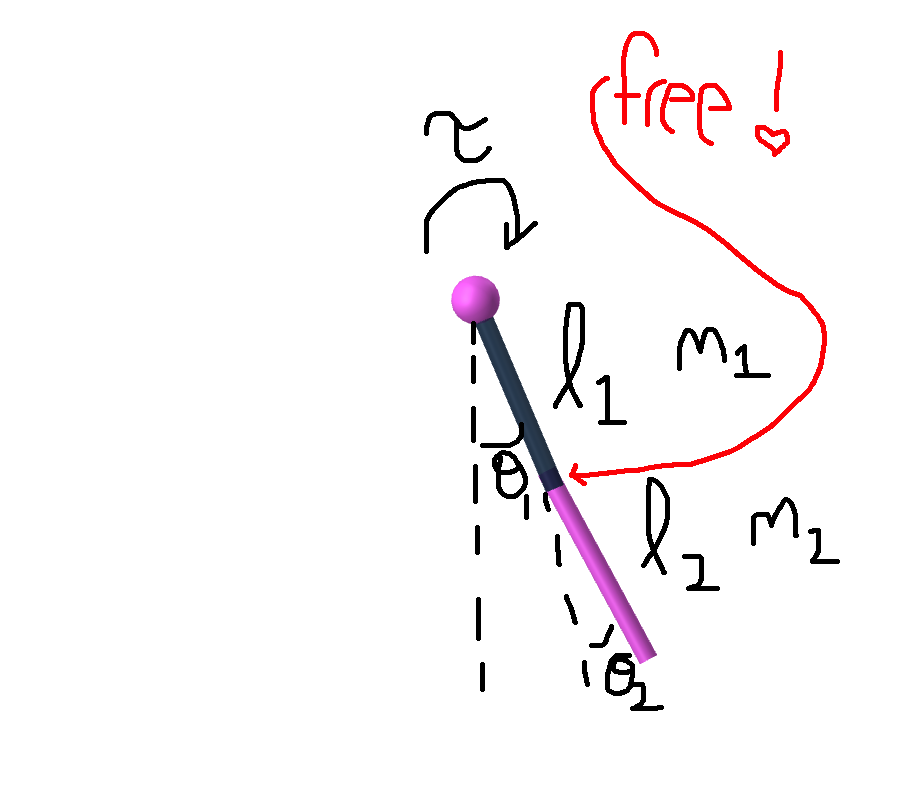
This is the Pendubot! For the rest of this section, we’ll be using this notebook: https://deepnote.com/workspace/machine-class-2024-84dabec7-d1f8-40ab-9cc4-f975b9417910/project/Miana-Smiths-Untitled-project-e3263c92-4ad3-4793-8a7e-b0399bfbc995/notebook/Pendubot-0df799c8b2a6483d96083d1e4cfa3db2

Which should let you run the code and see the outputs and such!

We’ll be discussing LQR stabilization, trajectory optimization, finite horizon LQR, system ID, and more, using the above Pendubot with Drake.

Model predictive control

https://fab.cba.mit.edu/classes/865.18/control/model_based_control/index.html

And then, we’ve got our real Pendubot that we’re running off of LQR gains from the above notebook. So pop on over to here for a good time.

If you’d like to go more into the mathematics of optimization, you can review the 2021 course notes here: https://fab.cba.mit.edu/classes/865.21/topics/control/08_optimization.html… Or you could look in our search week homework from NMM (https://fab.cba.mit.edu/classes/864.23/people/index.html) because Neil made us do this as a pset lmao. With the above notebook, we’re using the included solvers instead of rolling our own. Sorry Neil?