Ring resonator

There are many ways to estimate the dielectric constant of a substrate. This paper describes the use of a ring resonator for this: Dielectric Characterization of PCB Laminate Materials Using Improved Capacitive Coupled Ring Resonators

The resonator consists of an input port and an exit port, with a ring of a given radius in between. The ring has capacitive coupling to the input and outputs, and is designed to resonate at a predefined frequency, given an initial estimate of the permittivity of the subtrate. The true resonance frequency of the ring can then be measured using a vector network analyser (VNA), leading to a revised value of the premittivity.

Cabrera et al. provide this helpful diagram, showing all the geometric parameters of the resonator: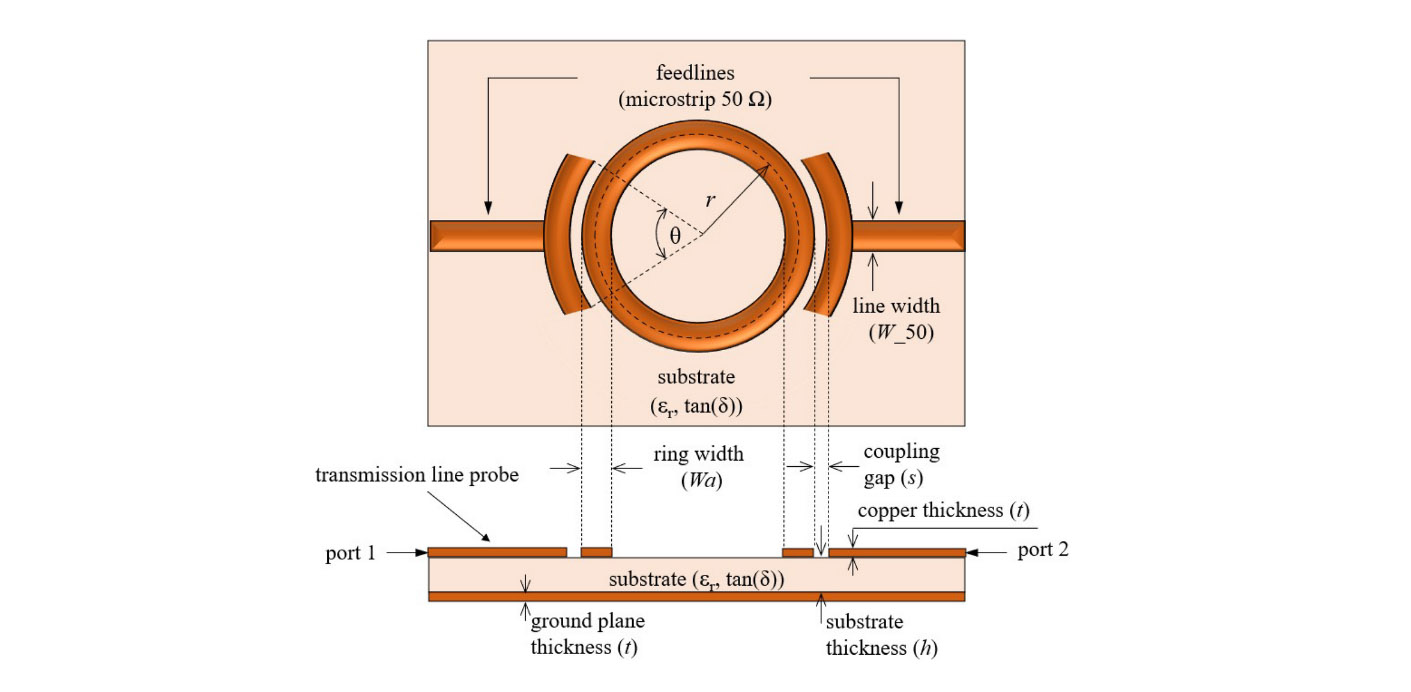

Theory

\[\lambda = \frac{2 \pi r}{n}\] \[\lambda = \frac{c}{f}\]

Neglecting tangent loss effects, the corrected speed of the wave is given by:

\[c = \frac{1}{\sqrt{\epsilon_r \epsilon_0 \mu_0}} = \frac{c_0}{\sqrt{\epsilon_r}}\]

Which gives us a compact formula for estimating $\epsilon_r$ from the observed resonance frequency $f$:

\[\epsilon_r = \left(\frac{c_0}{2 \pi r f}\right)^2\]

Implementation

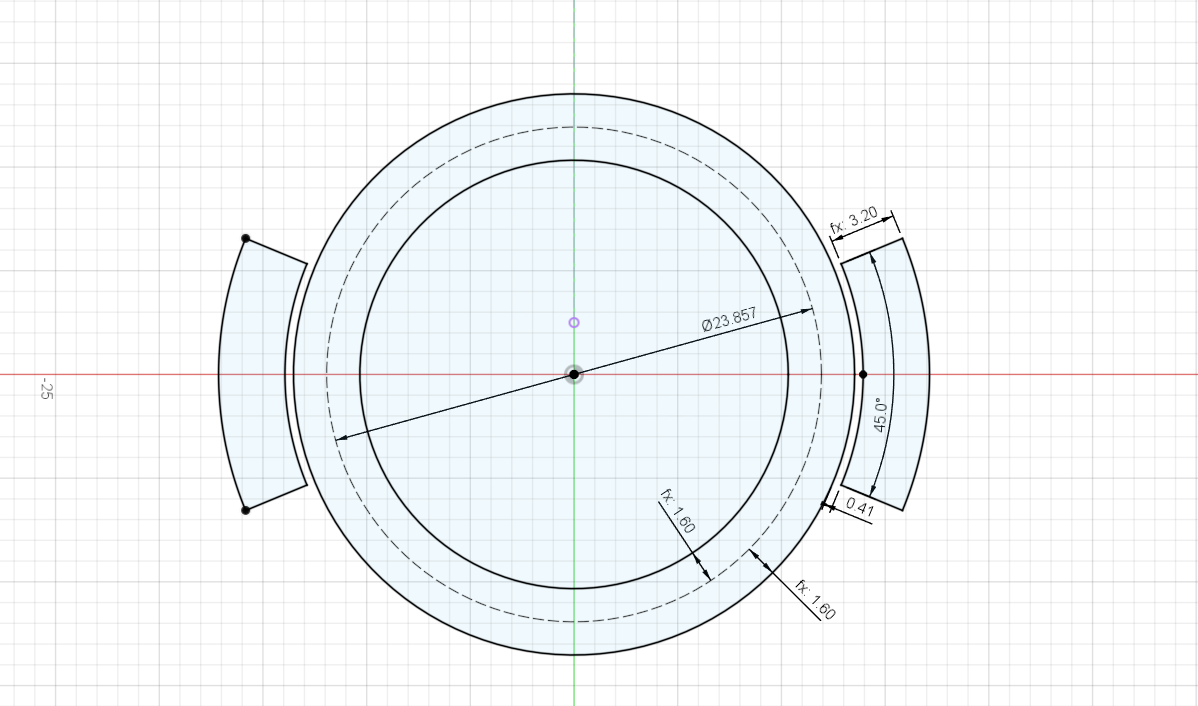
Following the method described by Cabrera et al., I designed a ring resonator with the following parameters:

• Radius: 11.9285 mm
• Trace width: 3.2 mm
• Trace gap: 0.41 mm

Those parameters should provide a resonance at $f = 2$ GHz for a dielectric with a $\epsilon_r=4$.

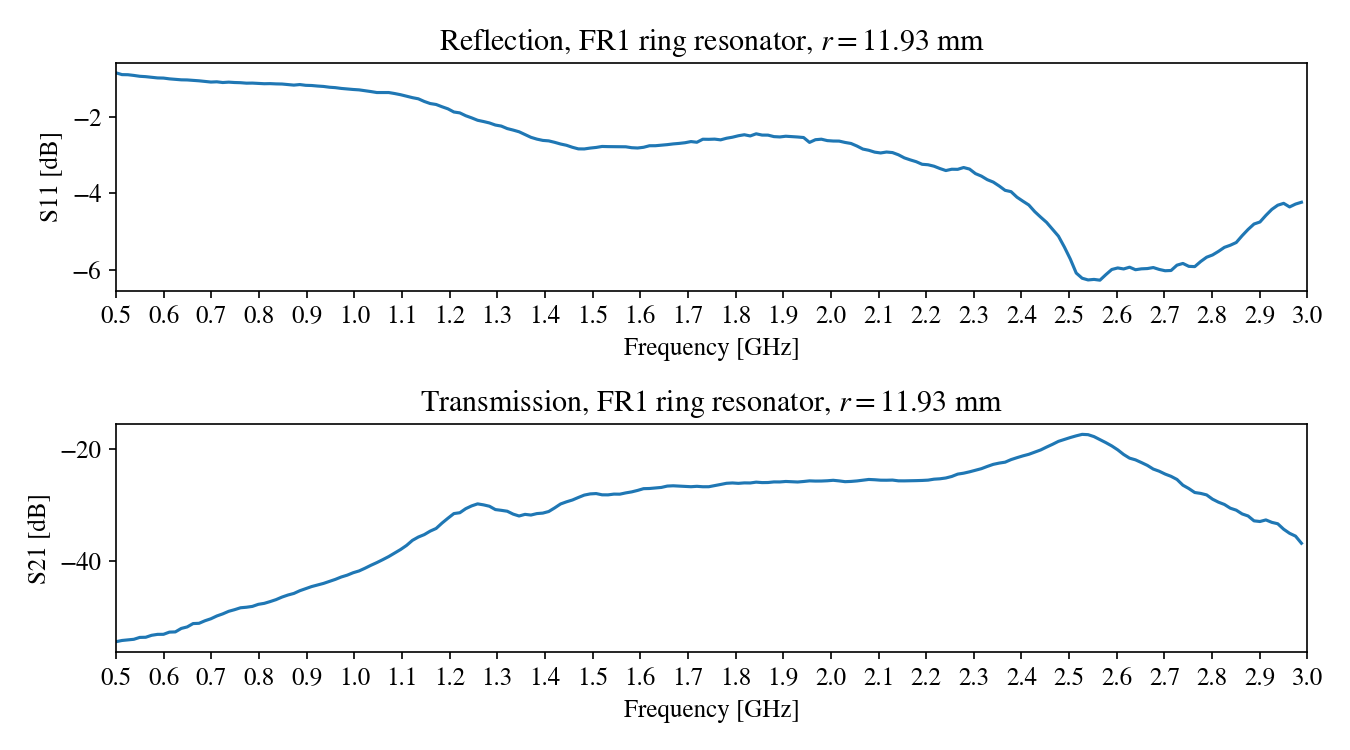
Results on FR1

I fabricated the design by milling a FR1 board. Here is the resulting board, complete with UFL connectors and copper braid connected to the ground plane below:

To measure the resonance profile, I used the NanoVNA-F V2, connecting the device to both TX and RX:

The transmission shows a clear peak at 2.53 GHz! This provides a corrected $\epsilon_r$ value of 2.5, which is in good agreement with previous observations:

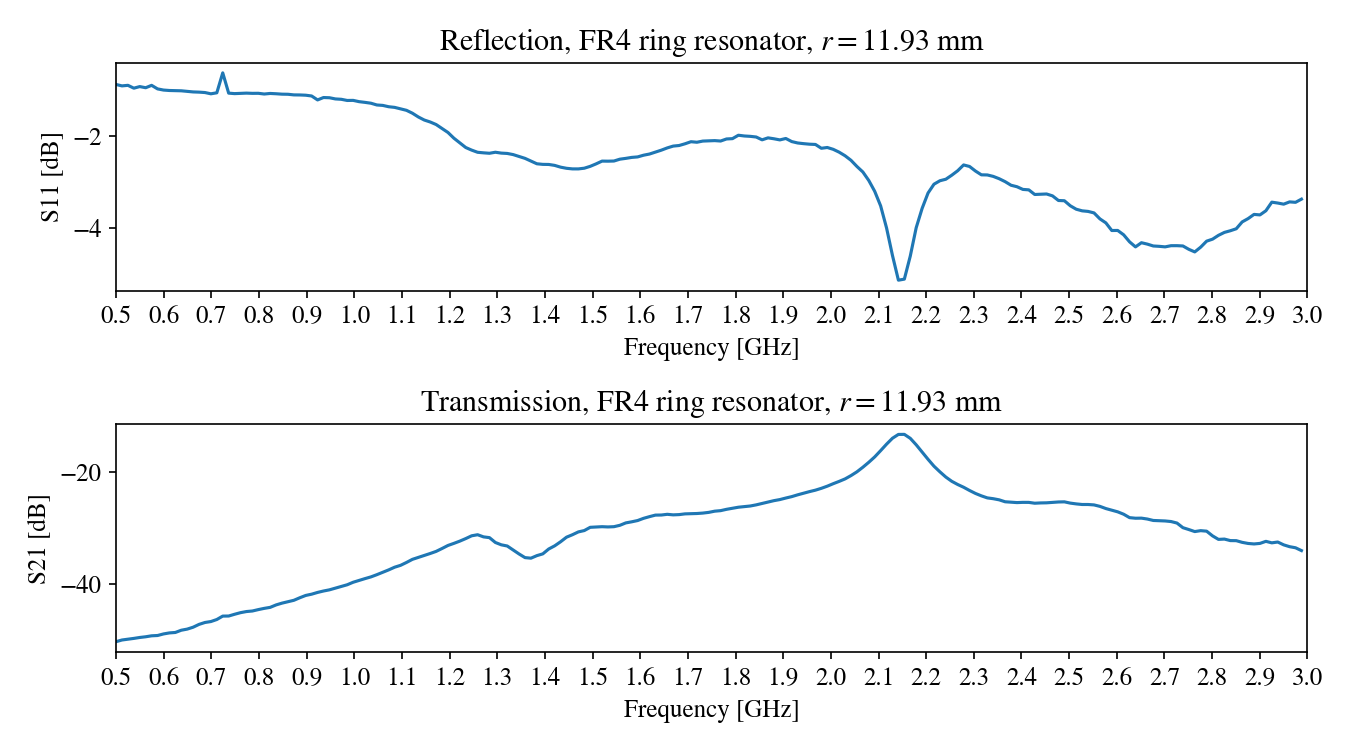
Results on FR4

For most of my experiments, I stuck to FR1 as it is more safe to handle and machine. My friend Nik kindly made a FR4 version of the ring resonator by laser machining on the xTool F1 we have:

Once again, I connected it to the VNA to measure the resonance:

The peak is at 2.148 GHz, giving us $\epsilon_r = 3.47$, which is lower than the 4 that was initially assumed, but higher than with FR1.