Week 1 - Dual Regular Polyhedra
How to Make (Almost) Anything - Manolis Zampetakis
Plan
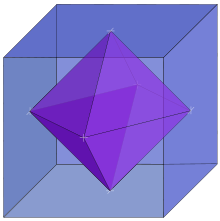
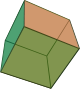
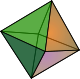
The assignment for this week was to make something 3D using cardboard as material and the laser cutter in order to cut it. Our idea for this assignment was to fabricate Platonic Solids illustrating their duality properties.The Platonic Solids are the only regular convex polyhedra and they are only five: Tetrahedron(triangular pyramid), Hexahedron(cube), Octahedron, Dodecahedron and Icosahedron. We can see these solids in the next figures.
| Tetrahedron | Hexahedron | Octahedron | Dodecahedron | Icosahedron |
|---|---|---|---|---|
 |
 |
 |
 |
 |
Now we explain what it means the duality for the polyhedra. This duality comes from the definition of duality in graph theory between two planar graphs. The idea is that starting from a polyhedron at each corner we attach a plane that is perpedicular to the line that connects this corner with the center of the polyhedron. Then these planes will intersect at some points and these points are the boundary of the dual polyhedron.
The first interesting fact about the dual polyhedra is that the dual of a regular polyhedron is also regular! Therefore starting from any of the above five polyhedra and taking the dual we will end up with another one of these five. Finally one amazing result is that if we take the dual polyhedron twice then we end up with the initial polyhedron!
Therefore we have the following pairs of dual polyhedra:
| Primal |  |
 |
 |
 |
 |
|---|---|---|---|---|---|
| Dual |  |
 |
 |
 |
 |
Design
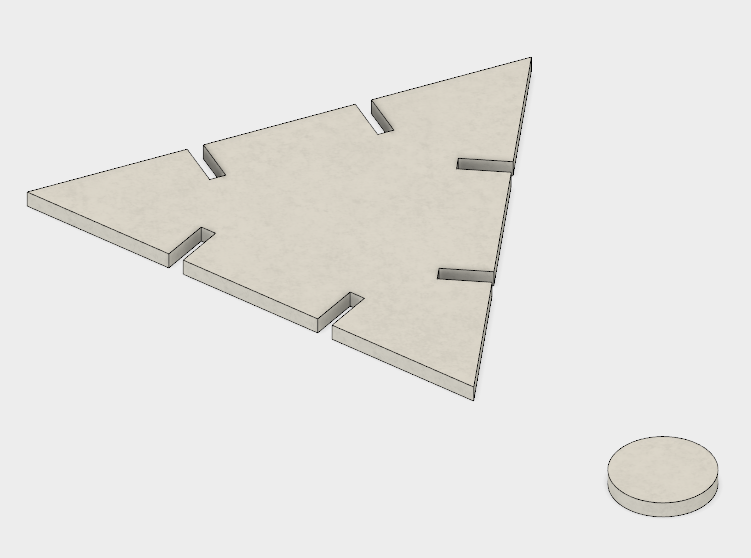
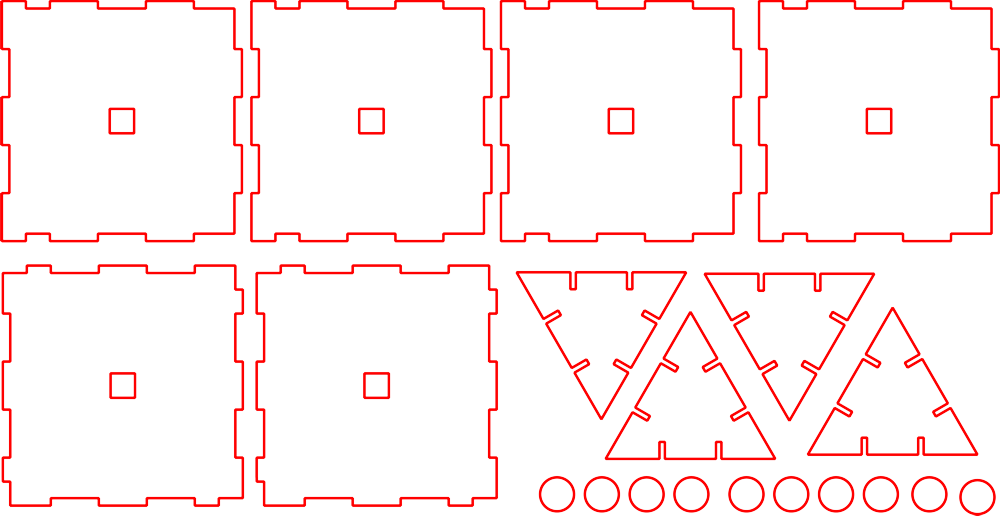
We initiate our design by making a 3D sketch of the hexahedron in the Fusion 360 program.
Then we did the same same for the side of the octahedron.
Finally we exported these sketches as DXF files to CorelDraw in order to print them to the laser cutter.
Construction
We finally show was the construction procedure